Content
Pollard's p-1 Method
Characteristic of Pollard's p-1 Method by Smooth Number
Pollard's P-1 Methed by Smooth Number Example 3
Pollard's p-1 Method
Pollard's p-1 method is a prime factorization algorithm discovered by John Pollard in 1974. Limited by the algorithm, the Pollard's p-1 method is only work for integers with specific factors.
However, since the composite number n is an unknown, sometimes, the algorithm may return a false response.
Characteristic of Pollard's p-1 Method by Smooth Number
The advantage of Pollard's p-1 method by smooth number is the checking of a group of primes with one computation. Every boundary B represents a group of numbers that can be expressed as the product of primes less than and equal to number B.
For example, a composite number n less than 10000 should have a prime factor less than √n=100. And primes within 100 are
| Primes | Integer | B-smooth | count |
|---|---|---|---|
| 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97 | p | 25 | |
| 2, 3, 5, 17 | p-1 | 2 | 4 |
| 2, 3, 5, 7, 13, 17, 19, 37, 73, 97 | p-1 | 3 | 10 |
| 2, 3, 5, 7, 11, 13, 17, 19, 31, 37, 41, 61, 73, 97 | p-1 | 5 | 14 |
| 2, 3, 5, 7, 11, 13, 17, 19, 29, 31, 37, 41, 43, 61, 71, 73, 97 | p-1 | 7 | 17 |
| 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 61, 67, 71, 73, 89, 97 | p-1 | 11 | 20 |
| 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 53, 61, 67, 71, 73, 79, 89, 97 | p-1 | 13 | 22 |
| 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 53, 61, 67, 71, 73, 79, 89, 97 | p-1 | 17 | 22 |
| 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 53, 61, 67, 71, 73, 79, 89, 97 | p-1 | 19 | 22 |
| 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 61, 67, 71, 73, 79, 89, 97 | p-1 | 23 | 23 |
| 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 89, 97 | p-1 | 29 | 24 |
| 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 89, 97 | p-1 | 31 | 24 |
| 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 89, 97 | p-1 | 37 | 24 |
| 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97 | p-1 | 41 | 25 |
| 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97 | p-1 | 43 | 25 |
| 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97 | p-1 | 47 | 25 |
More primes can be included for checking by increasing the smoothness boundary B.
For checking n and ak-1 is divisible by p, k is selected sufficiently large to ensure p-1 divides k, If the specific type prime factor is less than กิn, in the worst case, the smoothness boundary B can be equal to 41.
However, since the composite number n is an unknown, sometimes, the algorithm may return a false response. For example:
Pollard's P-1 Methed by Smooth Number Example 3
For example: n=533=p*q=13*41; let B=5 imply
| Integer | B-smooth number | Prime Factors | number |
|---|---|---|---|
| k | 5 | 29*35*53 = 512*243*125 | 15552000 |
Therefore for B=5, k5 or (p5-1)m5 is equal to 15552000.
Fermat's Little Theorem
let a=2, by Fermat's little theorem, let p be one of the prime factors of n, imply p divides ak-1.
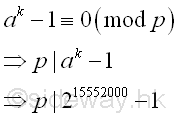
Greatest Common Divisor
Since ak-1 is a very large number, before finding the greatest common divisor of n and ak-1, ak-1 can be raised to the high power modulo n. Imply
Using squarings modulo
| base | number; a=2; k=15552000; n=533 |
|---|---|
| ak base 10 | 215552000 |
| ai base 10 | 21 = 21 ก 2 (mod 533) |
| 22 = 22 ≡ 4 (mod 533) | |
| 24 = 42 ≡ 16 (mod 533) | |
| 28 = 162 ≡ 256 (mod 533) | |
| 216 = 2562 ≡ 510 (mod 533) | |
| 232 = 5102 ≡ 529 (mod 533) | |
| 264 = 5292 ≡ 16 (mod 533) | |
| 2128 = 162 ≡ 256 (mod 533) | |
| 2256 = 2562 ≡ 510 (mod 533) | |
| 2512 = 5102 ≡ 529 (mod 533) | |
| 21024 = 5292 ≡ 16 (mod 533) | |
| 22048 = 162 ≡ 256 (mod 533) | |
| 24096 = 2562 ≡ 510 (mod 533) | |
| 28192 = 5102 ≡ 529 (mod 533) | |
| 216384 = 5292 ≡ 16 (mod 533) | |
| 232768 = 162 ≡ 256 (mod 533) | |
| 265536 = 2562 ≡ 510 (mod 533) | |
| 2131072 = 5102 ≡ 529 (mod 533) | |
| 2262144 = 5292 ≡ 16 (mod 533) | |
| 2524288 = 162 ≡ 256 (mod 533) | |
| 21048576 = 2562 ≡ 510 (mod 533) | |
| 22097152 = 5102 ≡ 529 (mod 533) | |
| 24194304 = 5292 ≡ 16 (mod 533) | |
| 28388608 = 162 ≡ 256 (mod 533) | |
| 216777216 = 5092 ≡ 285 (mod 533) | |
| 233554432 = 2852 ≡ 518 (mod 533) | |
| 267108864 = 5182 ≡ 190 (mod 533) | |
| ak base 10 | 28388608+4194304+2097152+524288+262144+65536+16384+2048+1024+512 |
| ak base 10 | 28388608*24194304*22097152*2524288*2262144* 265536*216384*22048*21024*2512 |
| ak base 10 | 256*16*529*256*16*510*16*256*16*529 ≡ 1 (mod 533) |
Imply
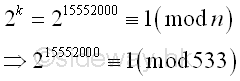
The algorithm returns a fail response, because the number n divides ak-1 and n is the greatest common divisor of n and ak-1. Imply
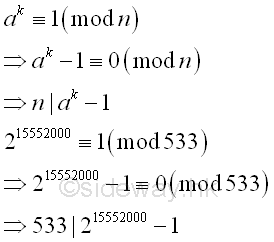
Therefore every prime factor of number n divides ak-1, imply
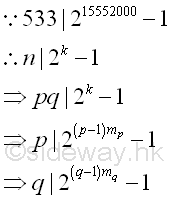
Since k is a very large number, usually the algorithm fails because k is the multiple of the product of p-1 and q-1, imply
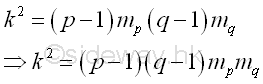
One way is to select a smaller k so that k is not the common multiple of both p-1 and q-1. Let B=3, Imply
| Integer | B-smooth number | Prime Factors | number |
|---|---|---|---|
| k | 3 | 29*35 = 512*243 | 124416 |
Therefore for B=3, k3 or (p3-1)m3 is equal to 124416.
Fermat's Little Theorem
let a=2, by Fermat's little theorem, let p be one of the prime factors of n, imply p divides ak-1.
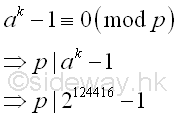
Greatest Common Divisor
Since ak-1 is a very large number, before finding the greatest common divisor of n and ak-1, ak-1 can be raised to the high power modulo n. Imply
Using squarings modulo
| base | number; a=2; k=124416; n=533 |
|---|---|
| ak base 10 | 2124416 |
| ai base 10 | 21 = 21 ก 2 (mod 533) |
| 22 = 22 ≡ 4 (mod 533) | |
| 24 = 42 ≡ 16 (mod 533) | |
| 28 = 162 ≡ 256 (mod 533) | |
| 216 = 2562 ≡ 510 (mod 533) | |
| 232 = 5102 ≡ 529 (mod 533) | |
| 264 = 5292 ≡ 16 (mod 533) | |
| 2128 = 162 ≡ 256 (mod 533) | |
| 2256 = 2562 ≡ 510 (mod 533) | |
| 2512 = 5102 ≡ 529 (mod 533) | |
| 21024 = 5292 ≡ 16 (mod 533) | |
| 22048 = 162 ≡ 256 (mod 533) | |
| 24096 = 2562 ≡ 510 (mod 533) | |
| 28192 = 5102 ≡ 529 (mod 533) | |
| 216384 = 5292 ≡ 16 (mod 533) | |
| 232768 = 162 ≡ 256 (mod 533) | |
| 265536 = 2562 ≡ 510 (mod 533) | |
| ak base 10 | 265536+32768+16384+8192+1024+512 |
| ak base 10 | 265536*232768*216384*28192*21024*2512 |
| ak base 10 | 510*256*16*529*16*529 ≡ 469 (mod 533) |
Imply
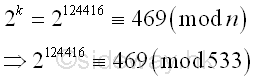
The greatest common divisor of n and ak-1 is
Using Euclid's algorithm
| ak-1 | n |
|---|---|
| 2124416-1 | 533 |
| 469-1 | 533 |
| 468 | 533-468=65 |
| 468-7*65=13 | 65 |
| 13 | 65-5*13=0 |
| 13 | 0 |
Imply
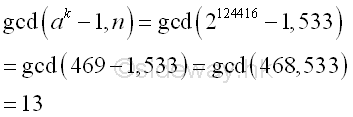
Integer 13, the greatest common divisor of n and ak-1 is also the prime divisor of n. And p-1 is 3-smooth.
| Integer | B-smooth number | Prime Factors | number |
|---|---|---|---|
| p-1 | 3 | 22*31 | 12 |
| k | 3 | 29*35 = 512*243 | 124416 |
| k/(p-1) | 27*34 | 10368 |
Besides, for B=5
| Integer | B-smooth number | Prime Factors | number |
|---|---|---|---|
| p-1 | 3,5 | 22*31 | 12 |
| q-1 | 5 | 23*51 | 40 |
| k5 | 5 | 29*35*53 = 512*243*125 | 15552000 |
| k5/(p-1)(q-1) | 24*34*52 | 32400 |
©sideway
ID: 120500008 Last Updated: 5/16/2012 Revision: 0
Latest Updated Links
- Travel Singapore Sight Space(last updated On 12/30/2025)
- Travel Singapore Sight Curiosity Cove(last updated On 12/30/2025)
- Travel Singapore Sight Night Safari(last updated On 12/30/2025)
- Travel Singapore Sight River Wonders(last updated On 12/30/2025)
- Travel Singapore Sight Rainforest Wild ASIA(last updated On 12/30/2025)
- Travel Singapore Sight Singapore Zoo(last updated On 12/30/2025)
- Travel Singapore Sight Mandai(last updated On 12/30/2025)
- Travel Singapore Sight Bird Paradise(last updated On 12/30/2025)
- Travel Singapore Sight AltitudeX(last updated On 12/30/2025)
- Travel Singapore Sight(last updated On 12/6/2025)
- Travel Singapore Rail Network(last updated On 12/5/2025)

 Nu Html Checker
Nu Html Checker  53
53  na
na  na
na
Home 5
Business
Management
HBR 3
Information
Recreation
Hobbies 9
Culture
Chinese 1097
English 339
Travel 31
Reference 79
Hardware 54
Computer
Hardware 259
Software
Application 213
Digitization 37
Latex 52
Manim 205
KB 1
Numeric 19
Programming
Web 289
Unicode 504
HTML 66
CSS 65
SVG 46
ASP.NET 270
OS 431
DeskTop 7
Python 72
Knowledge
Mathematics
Formulas 8
Set 1
Logic 1
Algebra 84
Number Theory 206
Trigonometry 31
Geometry 34
Calculus 67
Engineering
Tables 8
Mechanical
Rigid Bodies
Statics 92
Dynamics 37
Fluid 5
Control
Acoustics 19
Natural Sciences
Matter 1
Electric 27
Biology 1
