Content
Trigonometry
Angles
Measure of Angle
Degree Measure of Angle
Angles on Coordinate Plane
Radian Measure of Angle
Degree-Radian Conversion
Right-Angled Triangle
Trigonometric Functions
Pythagorean theorem
Values of Trigonometric Functions
Table of Trigonometric Functions for Common
Angles
More Values of Trigonometric Functions
Trigonometry
Trigonometry is the study of angles and the angular relationship of triangular figures. Although the relationship between an angle and the ratio of sides in a right triangle is one of the most important concept in trigonometry to define trigonometric functions, the applications of trigonometric functions of these relation are not limited on triangular or trigonometric matters.
Angles
An angle is formed by two rays with a common initial point. A ray is defined as a "half-line" line segment with an initial point from which the ray originates and an infinitely end point toward which the ray points. The common initial point of the two rays is called the vertex of the angle. Therefore the angle of a triangular figure at a specified point can be measured by the angular rotation between the initial side of the initial position of the ray and the terminal side of the final location of the ray about the vertex. Imply
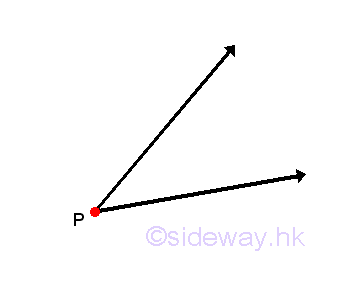
Measure of Angle
The amount of angular rotation between the initial and terminal rays is measured by a number. In some typical case, the two rays may coincide with each other in the same direction then the angle measure is zero. Or the two ray may be along the same line in opposite direction then the angle measure is a striaght angle. The initial ray can rotate either closewise or counter-clockwise to the position of the terminal ray. There are two ways to consider the rotation angle with positive angle is generated by counter-clockwise rotation and negative angle is generated by clockwise rotation. Although measure of an angle is usually in absolute value, oriented or signed angles, also callede directed, sensed angles, are also commonly used when the direction of rotation is important. Imply
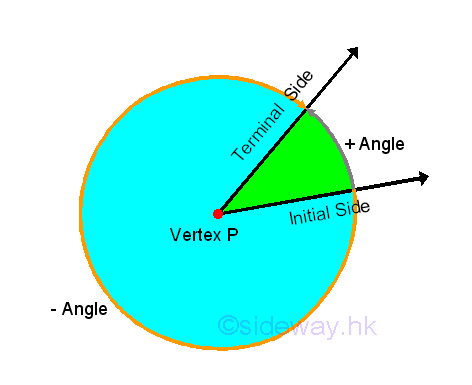
Degree Measure of Angle
One common angle measuring unit is degree measure with notation "o". This is not a SI unit. But degree measure is a common accepted unit for the description of an angle numerically especially in trigonomety study. One degree unit is defined by dividing one complete revolution of the initial side back to the initial side by 360 parts. Therefore one complete revolution is equal to 360o and parts of a revolution are measured proportionately. Since the initial side coincides with the terminal side, a 0 degree rotation or no rotation at all is equal to a 360 degee rotation and a 360 degree rotation is same as a -360 degree rotation. A striaght angle is equal to one half of a complete revolution, that is (360o)/2=180o. As the location of terminal side is the same, when the initial side rotates a half revolution in either clockwise or counter-clockwise direction, a 180 degree rotation is same as a -180 degree rotation. A quarter of a complete revolution is called a right angle is equal to (360o)/4=90o. For an angle which measures between 0o and 90o, is called an acute angle. For an angle which measures between 90o and 180o, is called an obtuse angle. When the sum of two angles is equal to 90o, the two angles are complementary angles. When the sum of two angles is equal to 180o, the two angles are supplementary angles. Angle measure less than one degree can be subdivide into decimal degrees or convertng to the Degree-Minute-Second (DMS) form. In the Degree-Minute-Second (DMS) system, one degree is divided into sixty minutes with notation " ' " equally, and one minute is further subdivided into sixty seconds with notation " " " equally also. That is 1o=60'=3600". Besides, for the represntation of rotational motion more than one revolution, angle measure can be more than 360o.
Angles on Coordinate Plane
In order to express an angle algebrically, an angle can be overlayed on the coordinate plane by locating the vertex of an angle on the origin and coinciding the initial side with the positive x-axis, that is in the standard position. Therefore, angle in standard position can be classfied according to the location of the terminal side of the angle, that is the four quadrants, I, II, III, and IV, of the coordinate plane. For example, angle with terminal side lies in quadrant I is called a quadrant I angle. And angle with terminal side lies on the coordinate axis is called quadrantal angle. When two standard angles are with the same initial and terminal sides, the two angles are coterminal angles. Since two angles share the same initial and terminal sides, the difference of the two coterminal angle is equal to 360o or -360o. Since the terminal side of an angle always repeats on a multiple of 360o, therefore two coterminal angles always differ by a multiple of 360o, that is difference of coterminal angles, α-β=n*(360o). As there are infinitely many integers n, a given angle also has infinitely many coterminal angels.
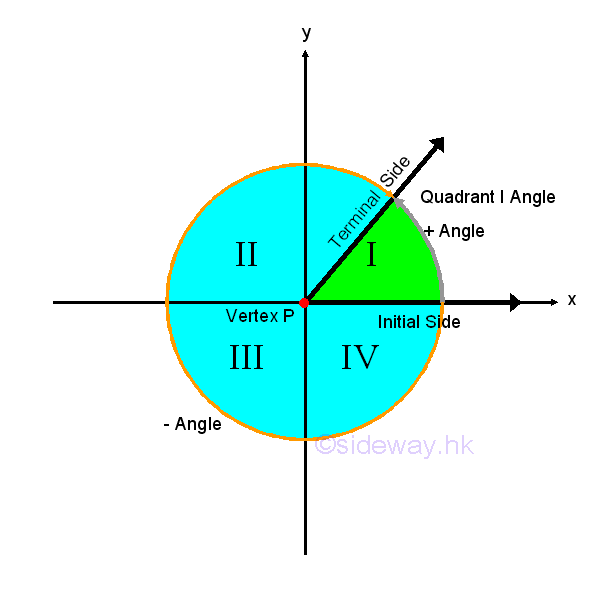
Radian Measure of Angle
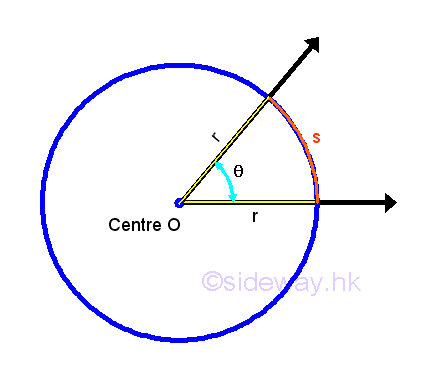
The radian measure is related with the geometry of a circle. This is a SI unit. The radian measure is an important unit for the description of an angle geometrically especially in the applications of trigonometric functions as ciruclar functions. By definition, the real number π is equal to the raito of the circumference of a circle, C over the diameter, d of the circle, that is π=C/d. Since diameter=2*radius, imply π=C/2r, or 2π=C/r, or r=C/2π. Considering a portion of the circle of radius, r with arc length,s and the central subtended angle by the arc is equal to θ, the ratio of the arc length, s over the radius of the circular arc is also a constant., that is θ=s/r. In other words, parts of a complete circular revolution is proportional to the corresponding arc length of the circle circumference. The ratio of the circumference of a circle over the radius of the circle is defined as the radian measure of an angle over one complete revolution. that is C/r=2π/r=2π radian. Radian measure of angle does not has a unit notation and radian unit can also be dropped because by definition the radian measure of angle is the ratio of a length over another length and the unit of the ratio is dimensionless. However, the word radian can still be used to denote the dimensionless radian angle measure as needed for clarity. Angle of a half of a revolution is equal to 2π/4=π/2. And angle of a quarter revolution is equal to 2π/2=π. Radian measure also follow the rule of oriented angles, a counter-clockwise rotation with a positive sign and a clockwise rotation with a negative sign. Similar to degree measure, when the sum of two angles is equal to π/2, the two angles are complementary angles. When the sum of two angles is equal to 2π, the two angles are supplementary angles. And two coterminal angles always differ by a multiple of 2π, α-β=n*(2π).
Degree-Radian Conversion
Since the angle measure of one completer revolution is equal to 360 in degree or 2π in radian, two measuring unit can be convert to each other throught a proportional ratio. Angle with a degree measure can be converted to a radian measure by multiplying a proportional ratio of 2π radian/360 degree=π radian/180o. Or angle with a radian measure can be converted to a degree measure by multiplying a proportional ratio of 360 degree/2π radian=180o/π radian.
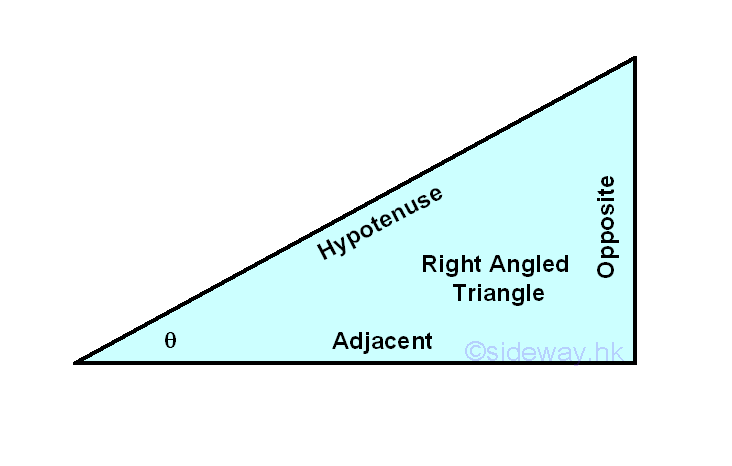
Right-Angled Triangle
The definition of Trigonometric functions are based on the relationship between the sides and the angle of a right or right- angled triangle. A right angled triangle is a triangle with one angle is a right angle. The sides of a triangle are named according the location of the specified angle. Opposite side is located opposite to the specified angle θ. Hypotenuse side is the longest side of the triangle. Adjacent side is located next to or adjacent to the specified angle θ.
Trigonometric Functions

The definition of the trigonometric functions based on a right or right- angled triangle are the length of one side divided by another side. The three main trigonometric functions are sine, cosine, and tangent functions. The sine function of A, denoted by sin A, is defined as the opposite side of A divided by the hypotenuse side of A. Imply
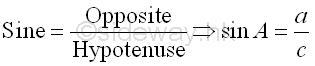
The cosine function of A, denoted by cos A, is defined as the adjacent side of A divided by the hypotenuse side of A. Imply

And the tangent function of A, denoted by tan A, is defined as the opposite side of A divided by the adjacent side of A. The sine, cosine and tangent functions of B can also be obtained accordingly. Imply

There are another three trigonometric functions which can be defined as the reciprocal functions of the above three functions correspondingly. The cosecant function of A, denoted by csc A, or cosec A, can be defined as the reciprocal of sine function of A and is equal to the hypotenuse side of A divided by the opposite side of A. Imply
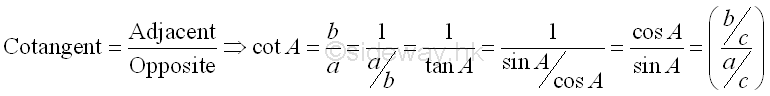
The secant function of A, denoted by sec A, can be defined as the reciprocal of cosine function of A and is equal to the hypotenuse side of A divided by the adjacent side of A. Imply
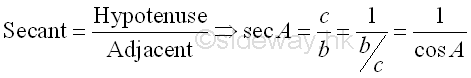
The cotangent function of A, denoted by cot A, can be defined as the reciprocal of tangent function of A and is equal to the adjacent side of A divided by the opposite side of A. Imply
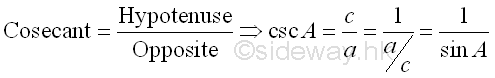
Pythagorean theorem
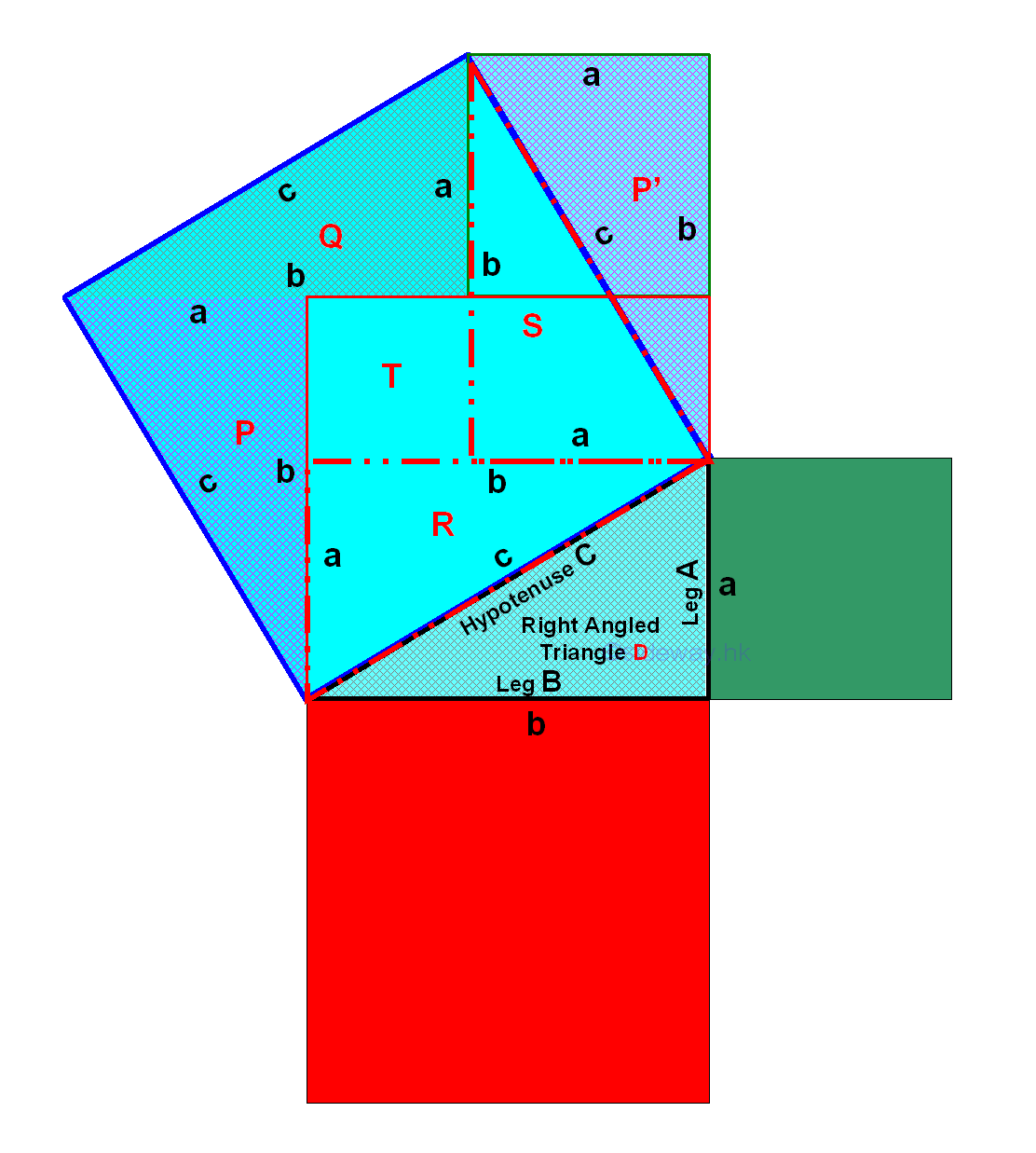
Pythagorean theorem or Pythagoras' theorem is the theorem about the relationship of the lengths of the three sides of a right angled triangle which can be used to find the values of trigonometric functions for some typical angles. Assumed the two sides next to the right angle are legs of length a and b, and the third side is the hypotenuse of length c. The Pythagorean theorem states that the sum of the squares of the lengths of the two legs of a right triangle is equal to the square of the length of the hypotenuse. That is a2+b2=c2. Imply
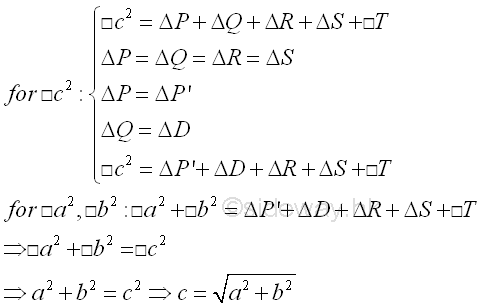
Values of Trigonometric Functions
Values of trigonometric functions for some typical angles can be determined by making use of some special types of triangles and the Pythagorean theorem geometrically. An equilateral triangle is a triangle with three equal sides and therefore the internal angles are also congruent angles and are equal to 60o. Let the lengths of sides of the equilateral triangle equal to c. By constructing a vertical perpendicular bisector from the top vertex, the equilateral triangle is divided into two equal parts with the bottem side of the equilateral triangle is divided into two equal parts of the same length. Let the length of the vertical bisector be a and the length of the bisected sides be b, then c=2b. Since the perpendicular bisector coincides with the angle bisector, the top vertex angle is also bisected into two equal angles, that is 30o=60o/2. Imply
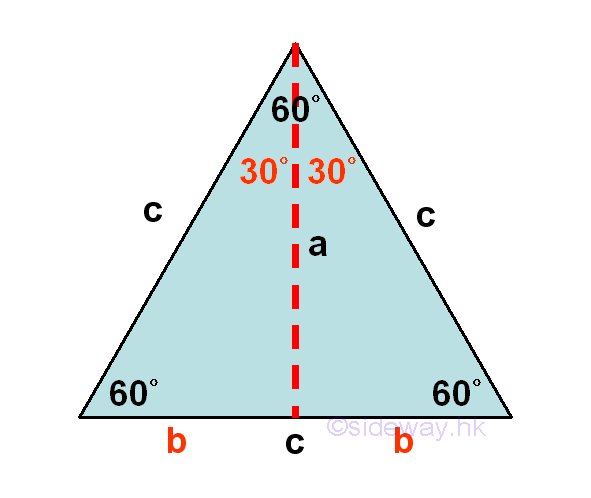
Since b can be expressed in term of c, that is b=c/2, a can also be found in term of c by making use of the Pythagorean theorem, that is a2+b2=c2⇒a=√(c2-b2). Imply
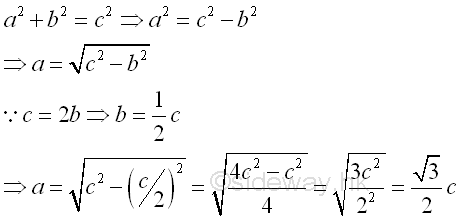
Therefore the relationships of the sides of a right-angled triangle of 30-60-90 degrees can be obtained. And the proportions of the sides can also simplified to a:b:c=(√3/2)c:(1/2)c:c=√3:1:2. Imply
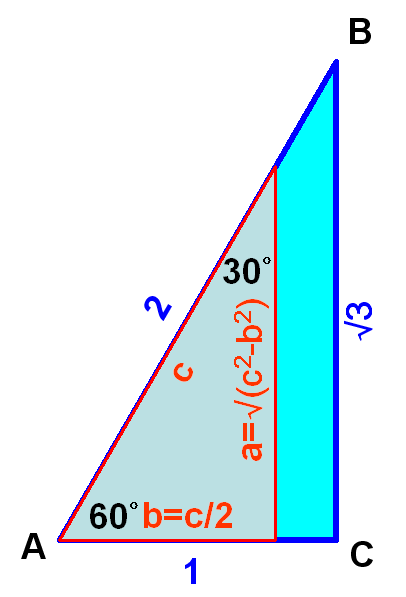
As the lengths of the sides of the 30-60-90 triangle are known, values of trigonometric functions for 30o and 60o can be found accordingly. Imply
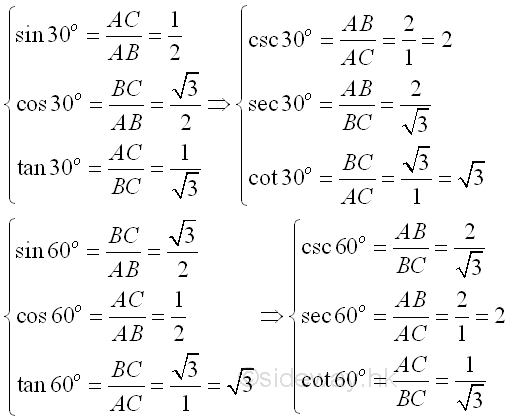
Consider an isosceles right-angled triangle of 45-45-90 degrees with two equal sides. Let the legs of the two equal sides next to the right angle are a and the third side of the hypotenuse be c.
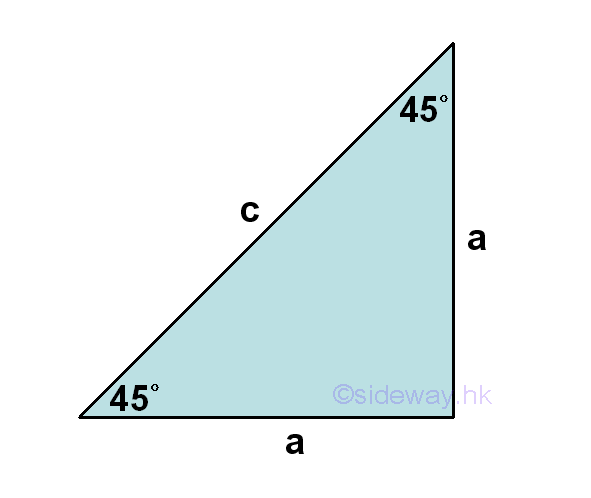
Since the triangle is already a right-angled triangle, Pythagorean theorem can be applied directly, that is that is a2+a2=c2⇒c=√(a2+a2)=√(2a2)=(√2)a . Imply

Therefore the relationships of the sides of a right-angled triangle of 45-45-90 degrees can be obtained. And the proportions of the sides can also simplified to a:a:c=a:a:(√2)a=1:1:√2. Imply
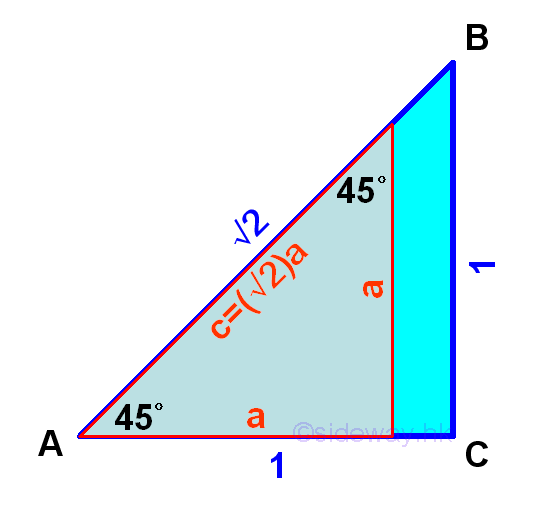
As the lengths of the sides of the 45-45-90 triangle are known, values of trigonometric functions for 45o can be found accordingly. Imply
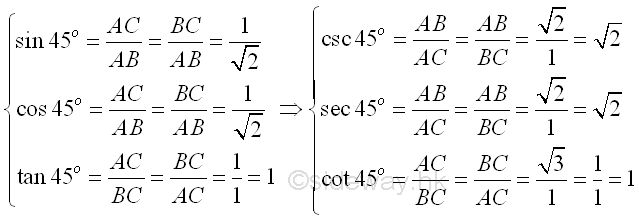
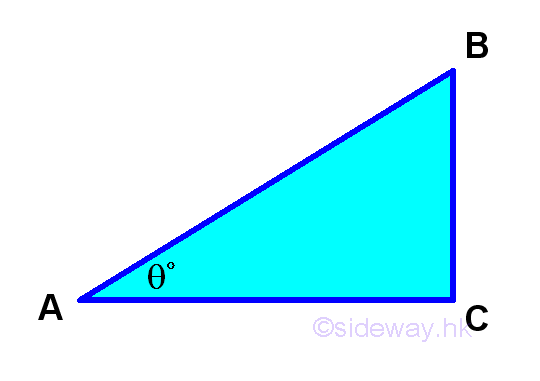
Similarly, values of trigonometric functions for 0o and 90o can also be found according to the definition of trigonometric function by constructing imaginary triangles, that is a triangle of zero height for 0o and a triangle of infinite height for 90o. Imply
Values of trigonometric functions for 0o and 90o are
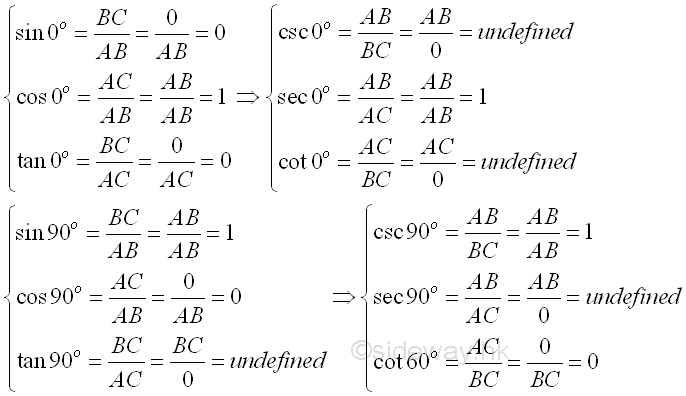
Table of Trigonometric Functions for Common Angles
| Degrees | Radians | sin θ | cos θ | tan θ | cot θ | sec θ | csc θ |
|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 0 | undefined | 1 | undefined |
| 30 | π/6 | 1/2 | √3/2 | √3/3 | √3 | 2√3/3 | 2 |
| 45 | π/4 | √2/2 | √2/2 | 1 | 1 | √2 | √2 |
| 60 | π/3 | √3/2 | 1/2 | √3 | √3/3 | 2 | 2√3/3 |
| 90 | π/2 | 1 | 0 | undefined | 0 | undefined | 1 |
| 120 | 2π/3 | √3/2 | -1/2 | -√3 | -√3/3 | -2 | 2√3/3 |
| 135 | 3π/4 | √2/2 | -√2/2 | -1 | -1 | -√2 | √2 |
| 150 | 5π/6 | 1/2 | -√3/2 | -√3/3 | -√3 | -2√3/3 | 2 |
| 180 | π | 0 | -1 | 0 | undefined | -1 | undefined |
| 210 | 7π/6 | -1/2 | -√3/2 | √3/3 | √3 | -2√3/3 | -2 |
| 225 | 5π/4 | -√2/2 | -√2/2 | 1 | 1 | -√2 | -√2 |
| 240 | 4π/3 | -√3/2 | -1/2 | √3 | √3/3 | -2 | -2√3/3 |
| 270 | 3π/2 | -1 | 0 | undefined | 0 | undefined | -1 |
| 300 | 5π/3 | -√3/2 | 1/2 | -√3 | -√3/3 | 2 | -2√3/3 |
| 315 | 7π/4 | -√2/2 | √2/2 | -1 | -1 | √2 | -√2 |
| 330 | 11π/6 | -1/2 | √3/2 | -√3/3 | -√3 | 2√3/3 | -2 |
| 360 | 2π | 0 | 1 | 0 | undefined | 1 | undefined |
More Values of Trigonometric Functions
By making use of the 45-45-90 and 30-60-90 triangles, trigonometric functions for 15o and 75o can also be found.
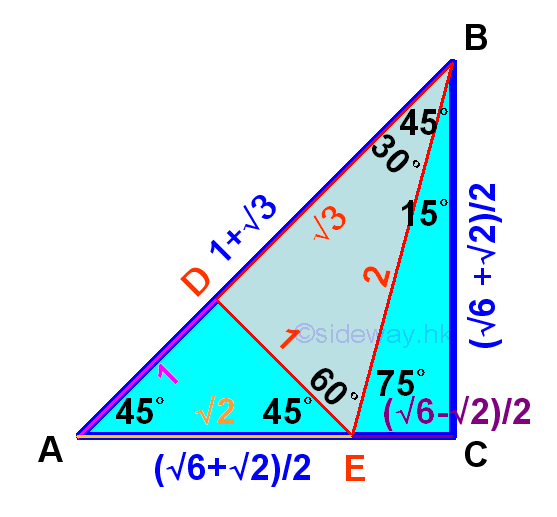
Assume ED=AD=1 and DE=2, and AC=BC, then length of sides of triangles can be determined as following:
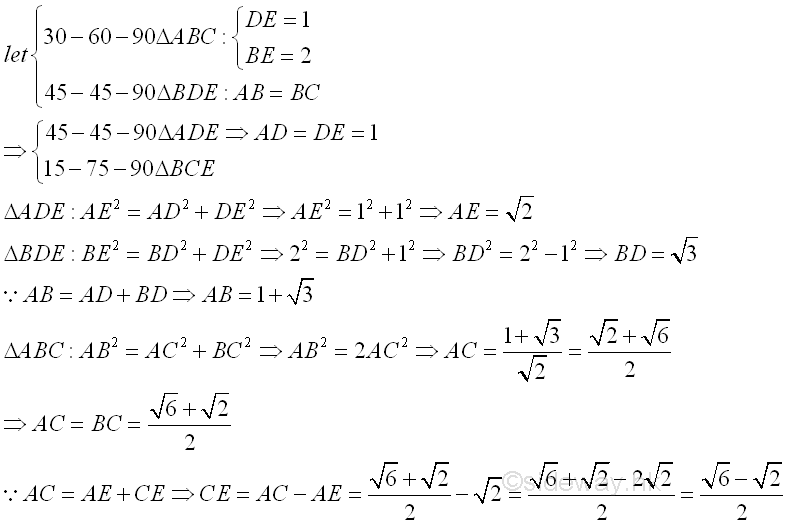
Values of trigonometric functions for 15o and 75o are
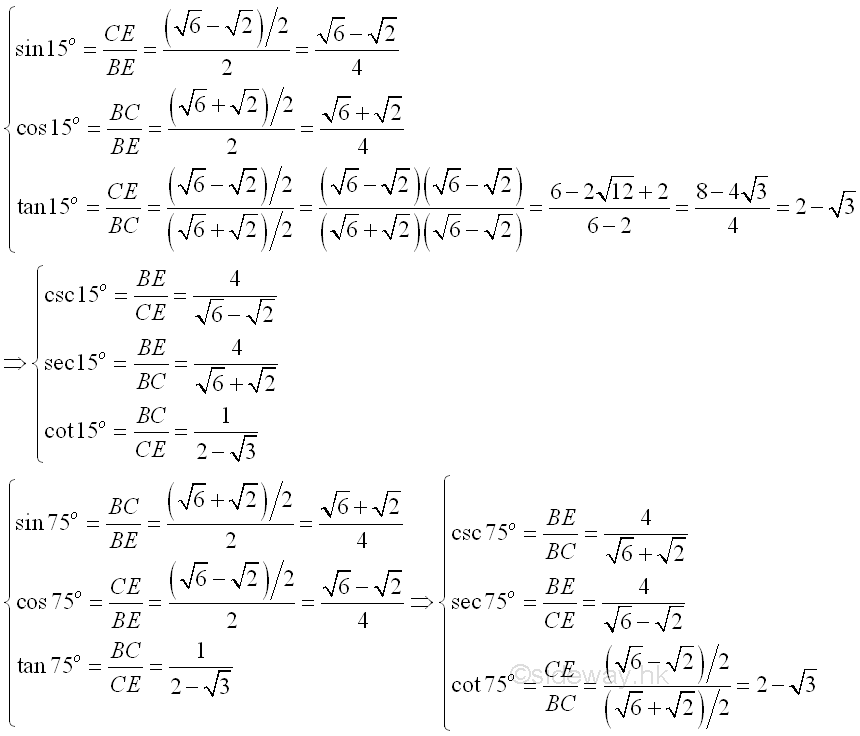
©sideway
ID: 130500023 Last Updated: 6/27/2013 Revision: 2 Ref:
References
- B. Joseph, 1978, University Mathematics: A Textbook for Students of Science & Engineering
- Ayres, F. JR, Moyer, R.E., 1999, Schaum's Outlines: Trigonometry
- Hopkings, W., 1833, Elements of Trigonometry
Latest Updated Links
- Travel Singapore Sight West | Central(last updated On 1/6/2026)
- Travel Singapore Sight Sentosa Sensoryscape(last updated On 1/5/2026)
- Travel Singapore Sight Sentosa Resorts World Sentosa(last updated On 1/4/2026)
- Travel Singapore Sight Sentosa HarbourFront(last updated On 1/3/2026)
- Travel Singapore Sight Sentosa(last updated On 1/2/2026)
- Travel Singapore Sight River Wonders(last updated On 12/30/2025)
- Travel Singapore Sight Bird Paradise(last updated On 12/30/2025)
- Travel Singapore Sight Mandai(last updated On 12/30/2025)
- Travel Singapore Sight Rainforest Wild ASIA(last updated On 12/30/2025)
- Travel Singapore Sight Night Safari(last updated On 12/30/2025)
- Travel Singapore Sight Curiosity Cove(last updated On 12/30/2025)

 Nu Html Checker
Nu Html Checker  53
53  na
na  na
na
Home 5
Business
Management
HBR 3
Information
Recreation
Hobbies 9
Culture
Chinese 1097
English 339
Travel 37
Reference 79
Hardware 54
Computer
Hardware 259
Software
Application 213
Digitization 37
Latex 52
Manim 205
KB 1
Numeric 19
Programming
Web 289
Unicode 504
HTML 66
CSS 65
SVG 46
ASP.NET 270
OS 431
DeskTop 7
Python 72
Knowledge
Mathematics
Formulas 8
Set 1
Logic 1
Algebra 84
Number Theory 206
Trigonometry 31
Geometry 34
Calculus 67
Engineering
Tables 8
Mechanical
Rigid Bodies
Statics 92
Dynamics 37
Fluid 5
Control
Acoustics 19
Natural Sciences
Matter 1
Electric 27
Biology 1
