Content
Approximation of Length of a Function
Curve Length of a Function
Approximation of Length of a Function
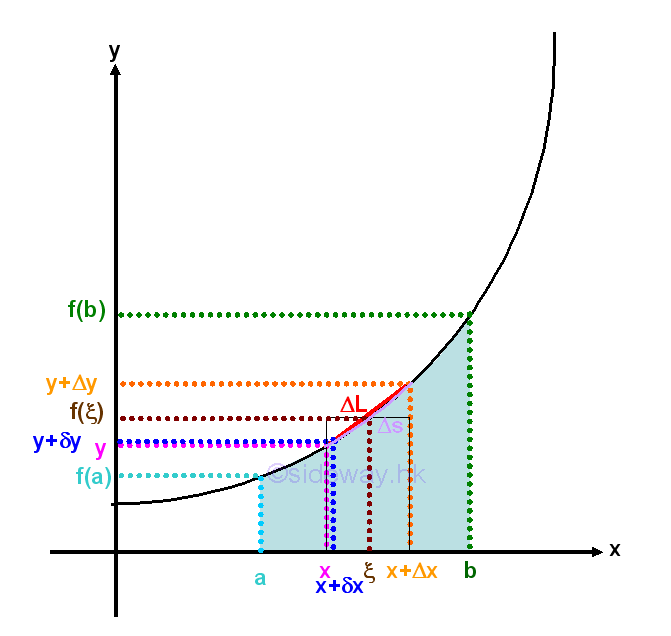
In general, the integral of a function is the approximation of the sum of function over a closed interval .
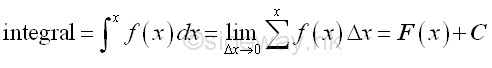
When Δx approaching zero, the limit exist and the integral converges to its instantaneous function with respect to the variable of integration. As Δx approaching zero, the length Δs of a function can also be approximated by the secant line ΔL of the infinitesimal curve element. Geometrically, the slope of the secant line is equal to the derivative of the function. Imply
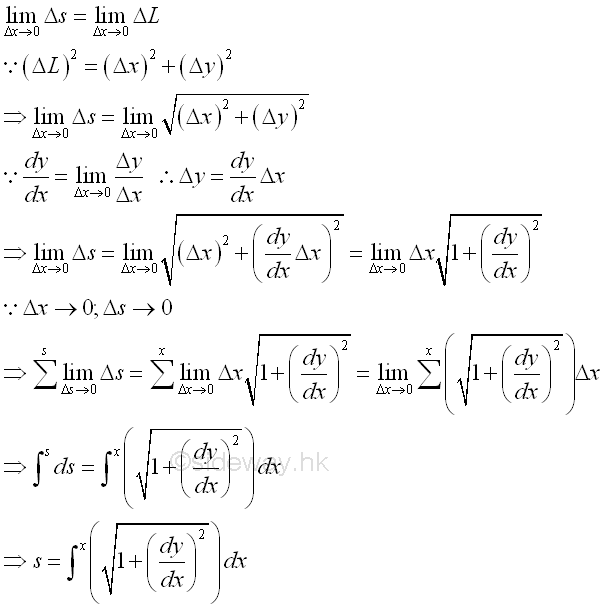
Curve Length of a Function
Therefore the curve length of a function over a closed interval can be determined by integration. For example, y=x3/2 [0,1]
Graphically,
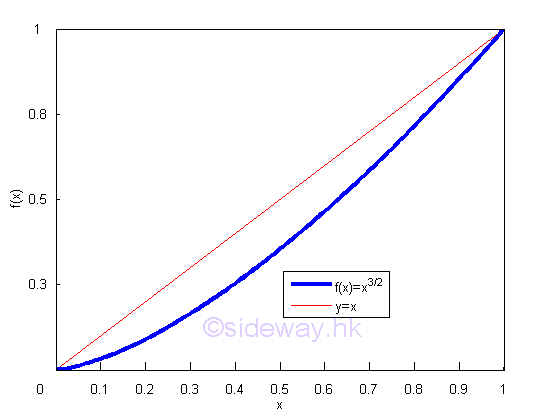
The curve length of function over a closed interval is
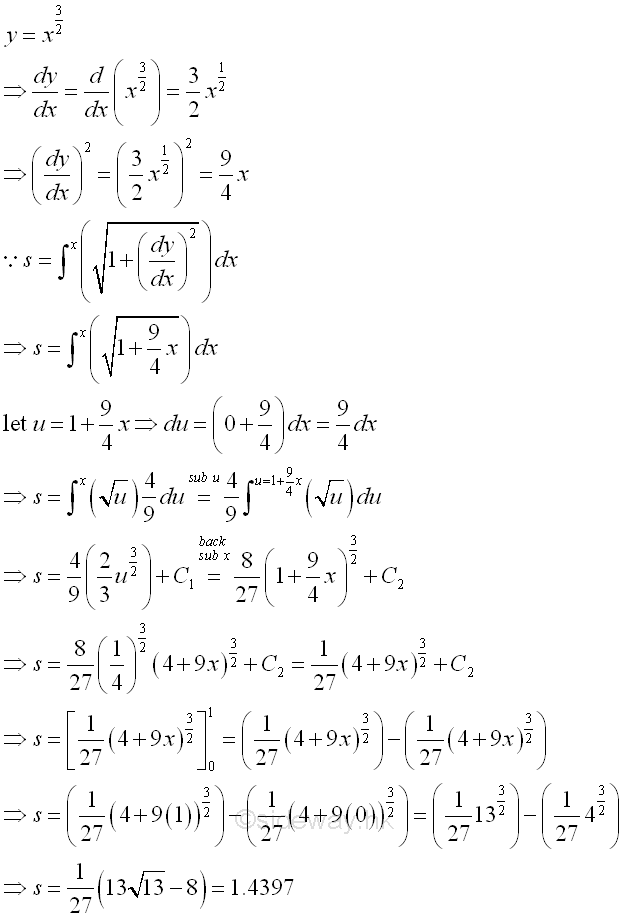
©sideway
ID: 120100015 Last Updated: 1/13/2012 Revision: 0 Ref:
References
- S. James, 1999, Calculus
- B. Joseph, 1978, University Mathematics: A Textbook for Students of Science & Engineering
Latest Updated Links
- Travel Singapore Sight Central(last updated On 1/8/2026)
- Panasonic HHGTQ1001B13 LED Floor Light(last updated On 1/7/2026)
- Travel Singapore Sight West | Central(last updated On 1/6/2026)
- Travel Singapore Sight Sentosa Sensoryscape(last updated On 1/5/2026)
- Travel Singapore Sight Sentosa Resorts World Sentosa(last updated On 1/4/2026)
- Travel Singapore Sight Sentosa HarbourFront(last updated On 1/3/2026)
- Travel Singapore Sight Sentosa(last updated On 1/2/2026)
- Travel Singapore Sight Bird Paradise(last updated On 12/30/2025)
- Travel Singapore Sight Mandai(last updated On 12/30/2025)
- Travel Singapore Sight Singapore Zoo(last updated On 12/30/2025)
- Travel Singapore Sight Rainforest Wild ASIA(last updated On 12/30/2025)

 Nu Html Checker
Nu Html Checker  53
53  na
na  na
na
Home 5
Business
Management
HBR 3
Information
Recreation
Hobbies 9
Culture
Chinese 1097
English 339
Travel 38
Reference 79
Hardware 55
Computer
Hardware 259
Software
Application 213
Digitization 37
Latex 52
Manim 205
KB 1
Numeric 19
Programming
Web 289
Unicode 504
HTML 66
CSS 65
SVG 46
ASP.NET 270
OS 431
DeskTop 7
Python 72
Knowledge
Mathematics
Formulas 8
Set 1
Logic 1
Algebra 84
Number Theory 206
Trigonometry 31
Geometry 34
Calculus 67
Engineering
Tables 8
Mechanical
Rigid Bodies
Statics 92
Dynamics 37
Fluid 5
Control
Acoustics 19
Natural Sciences
Matter 1
Electric 27
Biology 1
