Pollard's p-1 Method

Pollard's p-1 method is a prime factorization algorithm discovered by John Pollard in 1974. Limited by the algorithm, the Pollard's p-1 method is only work for integers with specific factors.

Pollard's p-1 Algorithm

For a composite integer, n, with a prime factor p, if p-1 can be expressed in terms of a product of primes and k is a multiple of p-1. By selecting an integer, a, which is greater than 1 and is coprime to n, then

 

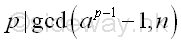
Imply

 

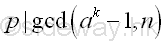
Since a is coprime to n, a is coprime to p also. Imply

 

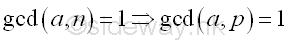
From Fermat's little theorem, if p does not divide a, then

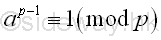
Similarly, If k is a multiple of p-1, then

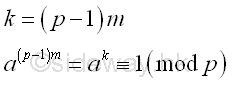
Imply p is a non-trivial divisor of ap-1-1 or ak-1 .

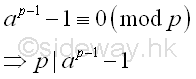  or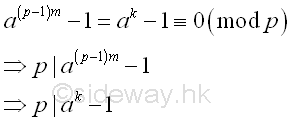

Since p is also a prime factor of n, p divides the greatest common divisor of  ap-1-1 or ak-1,  and n.

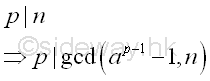  or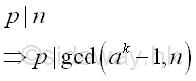

Therefore, if the greatest common divisor of  ak-1,  and n is greater than 1, the greatest common divisor is a factor of n also.

Pollard's p-1 Method

Although the Pollard's p-1 algorithm cannot be used to determine the prime factor p directly, the Pollard's p-1 method is an efficient prime factor finding method for composite integers with specific types of prime factors by choosing and testing some integers systematically.

Smooth Number Method

Smooth Number

One of the number choosing method for integer k is the making use of the concept of smooth number and the specific type of prime factor, i.e. p-1 is the product of primes.

Let x and B be integers. x is said to be B-smooth if all the prime divisors of n are less than or equal to B.

Example of Smooth Number

B	B-smooth numbers	Prime Factors
2,3,5,7,11,...	1	20,30,50,70,110,...
2,3,5,7,11,...	2	21,
3,5,7,11,...	3	31,
2,3,5,7,11,...	4	22,
5,7,11,...	5	51,
3,5,7,11,...	6	21,31,
7,11,...	7	71,
2,3,5,7,11,...	8	23,
3,5,7,11,...	9	32,
5,7,11,...	10	21,51,
11,...	11	111,
3,5,7,11,...	12	22,31,
7,11,...	14	21,71,
5,7,11,...	15	31,51,
2,3,5,7,11,...	16	24,
3,5,7,11,...	18	21,32,
3,5,7,11,...	24	23,31,
2,3,5,7,11,...	32	25,
2,3,5,7,11,...	64	26,
11,...	77	71,111,
5,7,11,...	120	23,31,51,
5,7,11,...	360	23,32,51,
5,7,11,...	1800	23,32,52,

Although B is usually a prime number, B can be a composite number providing that B is greater than or equal to the largest prime factor of x.  The key information from a B-smooth number is the prime factor of a number. However, there is no information on the power or index of the prime factor. The lowest B-smooth of a number is the greatest prime factor of the number.

Pollard's P-1 Methed by Smooth Number

Since p-1 divides k, by assuming p-1 is B-smooth, if k is also B-smooth then the choosen integer k should be sufficienly large to ensure p-1 divides k. Therefore k is the product of all  prime factors with powers less than and equal to B and the index or power ei  for each prime factor pi less than and equal to B of k should be just less than and equal to n. Imply

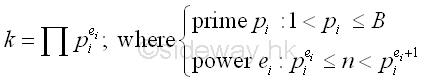
Pollard's P-1 Methed by Smooth Number Example 1

For example: n=203=p*q=7*29; let B=5 imply

Integer	B-smooth number	Prime Factors	number
k	5	27*34*53 = 128*81*125	1296000

Therefore for B=5, k5 or (p5-1)m5 is equal to 1296000.

Fermat's Little Theorem

let a=2, by Fermat's little theorem, let p be one of the prime factors of n, imply

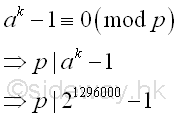
Greatest Common Divisor

Since ak-1 is a very large number, before finding the greatest common divisor of n and ak-1,  ak-1 can be raised to the high power modulo n. Imply

Using squarings modulo

base	number; a=2; k=1296000; n=203
ak base 10	21296000
ai base 10	21  = 21 ≡ 2 (mod 203)
	22 = 22 ≡ 4 (mod 203)
	24 = 42 ≡ 16 (mod 203)
	28 = 162 ≡ 53 (mod 203)
	216 = 532 ≡ 170 (mod 203)
	232 = 1702 ≡ 74 (mod 203)
	264 = 742 ≡ 198 (mod 203)
	2128 = 1982 ≡ 25 (mod 203)
	2256 = 252 ≡ 16 (mod 203)
	2512 = 162 ≡ 53 (mod 203)
	21024 = 532 ≡ 170 (mod 203)
	22048 = 1702 ≡ 74 (mod 203)
	24096 = 742 ≡ 198 (mod 203)
	28192 = 1982 ≡ 25 (mod 203)
	216384 = 252 ≡ 16 (mod 203)
	232768 = 162 ≡ 53 (mod 203)
	265536 = 532 ≡ 170 (mod 203)
	2131072 = 1702 ≡ 74 (mod 203)
	2262144 = 742 ≡ 198 (mod 203)
	2524288 = 1982 ≡ 25 (mod 203)
	21048576 = 252 ≡ 16 (mod 203)
ak base 10	21048576+131072+65536+32768+16384+1024+512+128
ak base 10	21048576*2131072*265536*232768*216384*21024*2512*2128
ak base 10	16*74*170*53*16*170*53*25 ≡ 197 (mod 203)

Using binary squarings modulo

base	number; a=2; k=1296000; n=203
k base 10	1296000
k base 2	(100111100011010000000)2
k base 10	220+217+216+215+214+210+29+27
ak base 10	21296000
ak base 10	2^220+2^217+2^216+2^215+2^214+2^210+2^29+2^27
ak base 2	10100111100011010000000
ai base 10; a=2	0:(1*(a^0))2 = a0 ≡ 1 (mod 203)
	1:(1*(a^1))2 = a2 ≡ 4 (mod 203)
	0:(a2*(a^0))2 = a4 ≡ 16 (mod 203)
	0:(a4*(a^0))2 = a8 ≡ 53 (mod 203)
	1:(a8*(a^1))2 = a18 ≡ 71 (mod 203)
	1:(a18*(a^1))2 = a38 ≡ 67 (mod 203)
	1:(a38*(a^1))2 = a78 ≡ 92 (mod 203)
	1:(a78*(a^1))2 = a158 ≡ 158 (mod 203)
	0:(a158*(a^0))2 = a316 ≡ 198 (mod 203)
	0:(a316*(a^0))2 = a632 ≡ 25 (mod 203)
	0:(a632*(a^0))2 = a1264 ≡ 16 (mod 203)
	1:(a1264*(a^1))2 = a2530 ≡ 9 (mod 203)
	1:(a2530*(a^1))2 = a5062 ≡ 121 (mod 203)
	0:(a5062*(a^0))2 = a10124 ≡ 25 (mod 203)
	1:(a10124*(a^1))2 = a20250 ≡ 64 (mod 203)
	0:(a20250*(a^0))2 = a40500 ≡ 36 (mod 203)
	0:(a40500*(a^0))2 = a81000 ≡ 78 (mod 203)
	0:(a81000*(a^0))2 = a162000 ≡ 197 (mod 203)
	0:(a162000*(a^0))2 = a324000 ≡ 36 (mod 203)
	0:(a324000*(a^0))2 = a648000 ≡ 78 (mod 203)
	0:(a648000*(a^0))2 = a1296000 ≡ 197 (mod 203)
ak base 10	21296000 ≡ 197 (mod 203)

and using the residue to calculate the greatest common divisor. Imply 

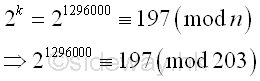
The greatest common divisor of n and ak-1 is

Using Euclid's algorithm

ak-1	n
21296000-1	203
197-1	203
196	203
196	203-196
196	7
196-7*28	7
0	7

Imply

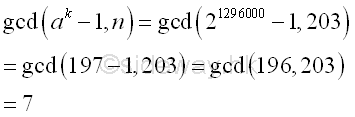
Integer 7, the greatest common divisor of n and ak-1 is also the prime divisor of n. And p-1 is  5-smooth.

Integer	B-smooth number	Prime Factors	number
p-1	3, 5	21*31	6
k	5	27*34*53 = 128*81*125	1296000
k/(p-1)		26*33*53	216000

Since the greatest prime factor of p-1 is 3-smooth also. And therefore the prime factor 7 can also be found by using B=3

Integer	B-smooth number	Prime Factors	number
p-1	3	21*31	6
k	3	27*34 = 128*81	10368
k/(p-1)		26*33	1728

let a=2, by Fermat's little theorem, imply p divides  210368-1 ≡ 168 (mod 203)

The greatest common divisor of n and ak-1 is gcd(168,203)= 7

And 7 is the prime divisor of n as before.