Content
Pollard's p-1 Method
PowerSmooth Number Method
PowerSmooth Number
Example of
PowerSmooth Number
Pollard's P-1 Methed by PowerSmooth Number
Pollard's P-1 Method by
PowerSmooth Number Example 1
Fermat's Little Theorem
Greatest Common Divisor
Pollard's p-1 Method
Pollard's p-1 method is a prime factorization algorithm discovered by John Pollard in 1974. Limited by the algorithm, the Pollard's p-1 method is only work for integers with specific factors.
One issue of the Pollard's p-1 method by smooth number is the value of k is usually much larger than needed in order to ensure p-1 divides k. Therefore alternative selection of k are developed to reduce the time of computation. Alternative methods of selection of k are
-
limit the index or power ei for each prime factor pi such that the prime power is just less than and equal to กิn.
-
let k equal to B!
-
let k equal to the least common multiple of 1,2,3,...B
Although these methods can reduce the value of k, there is also the possibility that the prime factor p with p-1 is B-smooth of a number n is excluded such that p-1 does not divide k.
PowerSmooth Number Method
PowerSmooth Number
Another number choosing method for integer k is the making use of the concept of powersmooth number and the specific type of prime factor, i.e. p-1 is the product of primes.
Let x and B be integers. x is said to be B-powersmooth if all the prime power for dividing n are less than or equal to B.
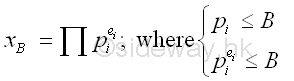
Example of PowerSmooth Number
| B | B-powersmooth numbers | Prime Factors |
|---|---|---|
| 2,3,4,5,6,7,8,9,10,11,... | 1 | 20,30,50,70,110,... |
| 2,3,4,5,6,7,8,9,10,11,... | 2 | 21, |
| 3,4,5,6,7,8,9,10,11,... | 3 | 31, |
| 4,5,6,7,8,9,10,11,... | 4 | 22, |
| 5,6,7,8,9,10,11,... | 5 | 51, |
| 3,4,5,6,7,8,9,10,11,... | 6 | 21,31, |
| 7,8,9,10,11,... | 7 | 71, |
| 8,9,10,11,... | 8 | 23, |
| 9,10,11,... | 9 | 32, |
| 5,6,7,8,9,10,11,... | 10 | 21,51, |
| 11,... | 11 | 111, |
Unlike smooth number, B is usually considered as the maximum boundry of a group of number. Therefore B can be prime number or composite number providing that B is greater than or equal to the largest prime power factor of x. The key information from a B-powersmooth number is the prime power factor of a number. The lowest B-powersmooth of a number is larger than or equal to the greatest prime power factor of the number.
Unlike B-smooth number, B-powersmooth number represents a finite set of numbers. Imply
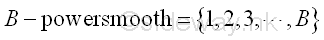
Therefore, x can be defined as the least common multiple of the numbers from 1 to B. Imply
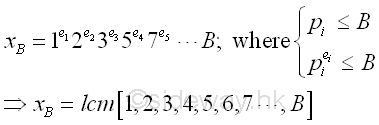
Pollard's P-1 Methed by PowerSmooth Number
Since p-1 divides k, by assuming p-1 is B-powersmooth, if k is also B-powersmooth then the choosen integer k should be sufficienly large to ensure p-1 divides k. Therefore k is equal to the least common multiple of all numbers less than and equal to B. Imply
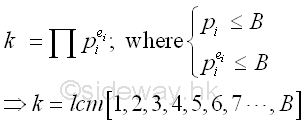
Let k equal to xB. Assume p-1 is B-powersmooth, then p-1 divides k.
Pollard's P-1 Method by PowerSmooth Number Example 1
For example: n=203=p*q=7*29; let B=5 imply
| Integern">Integer | B-powersmooth number | Prime Factors | number |
|---|---|---|---|
| k | 5 | 22*31*51 = 4*3*5 | 60 |
Therefore for B=5, kfor B=5, k5 or (p5-1)m5 is equal to 60.
Fermat's Little Theorem
let a=2, by Fermat's little theorem, let p be one of the prime factors of n, imply p divides ak-1.
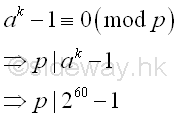
Greatest Common Divisor
Since ak-1 is a very large number, before finding the greatest common divisor of n and ak-1, ak-1 can be raised to the high power modulo n. Imply
Using squarings modulo
| base | number; a=2; k=60; n=203 |
|---|---|
| ak base 10 | 260 |
| ai base 10 | 21 = 21 ก 2 (mod 203) |
| 22 = 22 ≡ 4 (mod 203) | |
| 24 = 42 ≡ 16 (mod 203) | |
| 28 = 162 ≡ 53 (mod 203) | |
| 216 = 532 ≡ 170 (mod 203) | |
| 232 = 1702 ≡ 74 (mod 203) | |
| ak base 10 | 232+16+8+4 |
| ak base 10 | 232*216*28*24 |
| ak base 10 | 74*170*53*16 ≡ 190 (mod 203) |
Imply
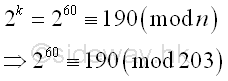
The greatest common divisor of n and ak-1 is
Using Euclid's algorithm
| ak-1 | n |
|---|---|
| 260-1 | 203 |
| 190-1 | 203 |
| 189 | 203 |
| 189 | 203-189 |
| 189 | 7 |
| 189-27*7 | 7 |
| 0 | 7 |
Imply
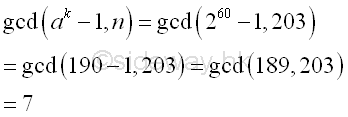
Integer 7, the greatest common divisor of n and ak-1 is also the prime divisor of n. And p-1 is 5-powersmooth.
| Integer | B-powersmooth number | Prime Factors | number |
|---|---|---|---|
| p-1 | 3, 5 | 21*31 | 6 |
| k | 5 | 22*31*51 = 4*3*5 | 60 |
| k/(p-1) | 21*30*51 | 10 |
Since the greatest prime power factor of p-1 is 3-smooth also. And therefore the prime factor 7 can also be found by using B=3
| Integer | B-powersmooth number | Prime Factors | number |
|---|---|---|---|
| p-1 | 3 | 21*31 | 6 |
| k | 3 | 21*31 = 2*3 | 6 |
| k/(p-1) | 20*30 | 1 |
let a=2, by Fermat's little theorem, imply p divides 26-1 ≡ 63 (mod 203)
The greatest common divisor of n and ak-1 is gcd(63,203)= 7
And 7 is the prime divisor of n as before.
©sideway
ID: 120500009 Last Updated: 5/17/2012 Revision: 0
Latest Updated Links
- Travel Singapore Sight Space(last updated On 12/30/2025)
- Travel Singapore Sight Curiosity Cove(last updated On 12/30/2025)
- Travel Singapore Sight Night Safari(last updated On 12/30/2025)
- Travel Singapore Sight River Wonders(last updated On 12/30/2025)
- Travel Singapore Sight Rainforest Wild ASIA(last updated On 12/30/2025)
- Travel Singapore Sight Singapore Zoo(last updated On 12/30/2025)
- Travel Singapore Sight Mandai(last updated On 12/30/2025)
- Travel Singapore Sight Bird Paradise(last updated On 12/30/2025)
- Travel Singapore Sight AltitudeX(last updated On 12/30/2025)
- Travel Singapore Sight(last updated On 12/6/2025)
- Travel Singapore Rail Network(last updated On 12/5/2025)

 Nu Html Checker
Nu Html Checker  53
53  na
na  na
na
Home 5
Business
Management
HBR 3
Information
Recreation
Hobbies 9
Culture
Chinese 1097
English 339
Travel 31
Reference 79
Hardware 54
Computer
Hardware 259
Software
Application 213
Digitization 37
Latex 52
Manim 205
KB 1
Numeric 19
Programming
Web 289
Unicode 504
HTML 66
CSS 65
SVG 46
ASP.NET 270
OS 431
DeskTop 7
Python 72
Knowledge
Mathematics
Formulas 8
Set 1
Logic 1
Algebra 84
Number Theory 206
Trigonometry 31
Geometry 34
Calculus 67
Engineering
Tables 8
Mechanical
Rigid Bodies
Statics 92
Dynamics 37
Fluid 5
Control
Acoustics 19
Natural Sciences
Matter 1
Electric 27
Biology 1
