Content
Anti-derivative of Physical Quantity
Linear Motion
Example of
Linear motion
Anti-derivative of Physical Quantity
In practical application, the interpretation of an indefinite integral as the anti-derivative of a function provides a mean for determining the physical qunatity when the physical quantity can be quantified in the form of infinitesimal elements.
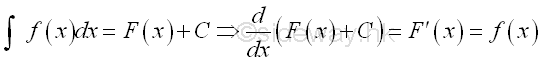
Anti-differentiation can also be applied to higher derivative. Through successive integration, related physical quantity functions can be determined.
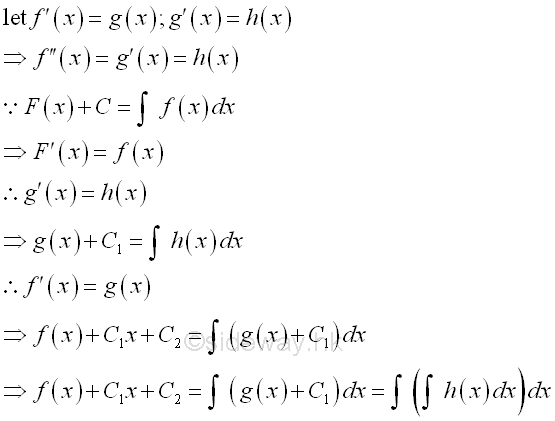
In order to determine the integration of constants, extra information, such as initial conditions, or boundary conditions are needed.
Linear Motion
The four variables to describe linear motion are acceleration a, velocity v, displacement s, and time t. Imply
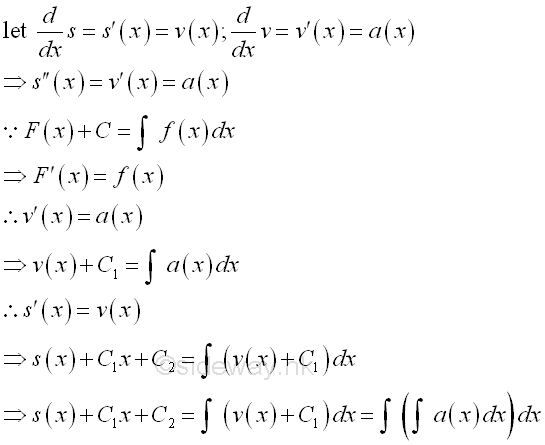
From the definition of acceleration, uniform acceleration is defined as the average velocity of an object over a period of time. imply
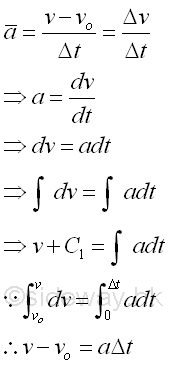
From the definition of velocity, uniform velocity is defined as the average displacement of an object over a period of time. imply
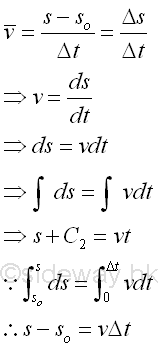
But for velocity with acceleration or deceleration, variable velocity is also a function of time. imply
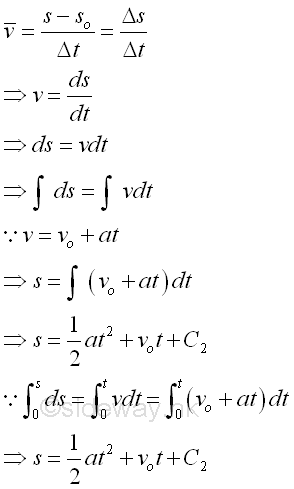
Example of Linear motion
A bullet is fired to a fixed board of thickness 5. The entering speed, vo is 10 and the leaving speed, v is 2. If the deceleration, a of the bullet is a constant, how much time, t is required to pass through the board and what it the thickness of the board required to stop the bullet from coming out.
Determine the acceleration first.
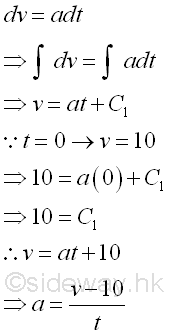
Since the velocity is decelerating, the velocity is a function of time, the time required is
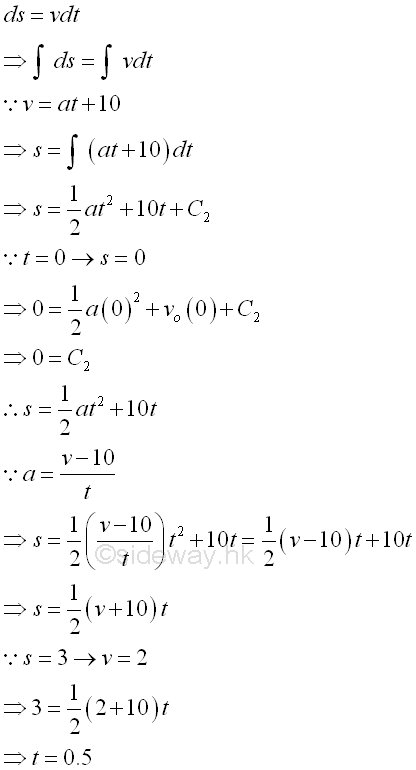
To determine the required thickness of the board to stop the bullet, determine the accelaration first, imply
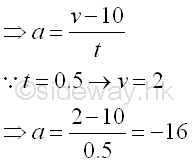
Using the same board to stop the bullet, imply v=0, and accelerarion is the same imply
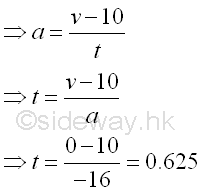
The required thickness is
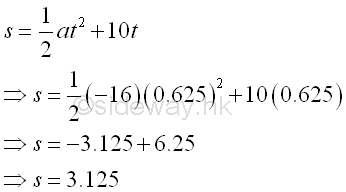
©sideway
ID: 120100013 Last Updated: 1/11/2012 Revision: 0 Ref:
References
- S. James, 1999, Calculus
- B. Joseph, 1978, University Mathematics: A Textbook for Students of Science & Engineering
Latest Updated Links
- Travel Singapore Sight Central(last updated On 1/8/2026)
- Panasonic HHGTQ1001B13 LED Floor Light(last updated On 1/7/2026)
- Travel Singapore Sight West | Central(last updated On 1/6/2026)
- Travel Singapore Sight Sentosa Sensoryscape(last updated On 1/5/2026)
- Travel Singapore Sight Sentosa Resorts World Sentosa(last updated On 1/4/2026)
- Travel Singapore Sight Sentosa HarbourFront(last updated On 1/3/2026)
- Travel Singapore Sight Sentosa(last updated On 1/2/2026)
- Travel Singapore Sight Bird Paradise(last updated On 12/30/2025)
- Travel Singapore Sight Mandai(last updated On 12/30/2025)
- Travel Singapore Sight Singapore Zoo(last updated On 12/30/2025)
- Travel Singapore Sight Rainforest Wild ASIA(last updated On 12/30/2025)

 Nu Html Checker
Nu Html Checker  53
53  na
na  na
na
Home 5
Business
Management
HBR 3
Information
Recreation
Hobbies 9
Culture
Chinese 1097
English 339
Travel 38
Reference 79
Hardware 55
Computer
Hardware 259
Software
Application 213
Digitization 37
Latex 52
Manim 205
KB 1
Numeric 19
Programming
Web 289
Unicode 504
HTML 66
CSS 65
SVG 46
ASP.NET 270
OS 431
DeskTop 7
Python 72
Knowledge
Mathematics
Formulas 8
Set 1
Logic 1
Algebra 84
Number Theory 206
Trigonometry 31
Geometry 34
Calculus 67
Engineering
Tables 8
Mechanical
Rigid Bodies
Statics 92
Dynamics 37
Fluid 5
Control
Acoustics 19
Natural Sciences
Matter 1
Electric 27
Biology 1
