Content
Slope of Tangent Line
Shape of Curve
Monotonicity
Concavity
Local Extreme Values
Slope of Tangent Line
When interpreting the derivative as the slope of tangent line at x, the derivative of function y can provide the gradient information about steepness of the graph of the function.
Shape of Curve
For some simple functions in domain [0,5], the function can be always increasing, remaining constant, or always decreasing.
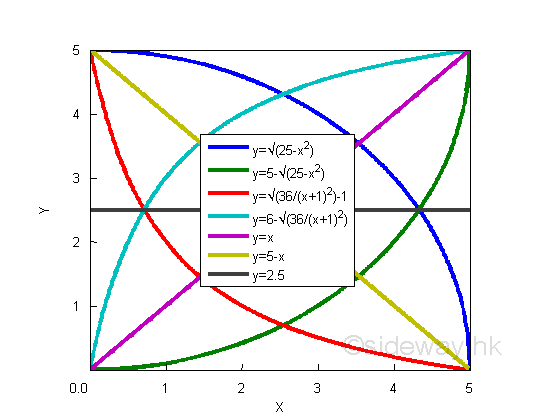
Monotonicity
For a monotonically increasing function y, the value of ratio Δy over Δx is always positive, therefore the value of derivaive is also always positive. The derivative of the straight line y=f(x)=x is equal to 1. The derivatives of curves in domain [0 5] are
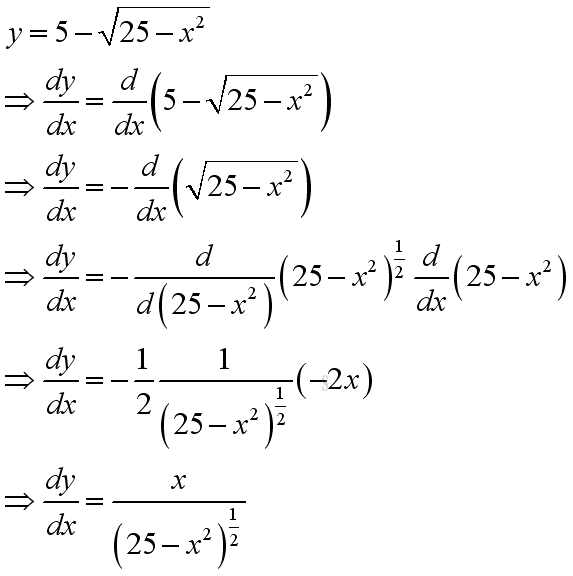 and
and
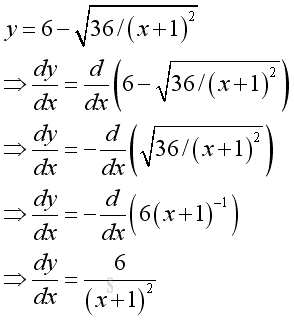
The angles of the tangent line are always less than π/2, therefore the slopes or their derivatives are always positive.
For a monotonically decreasing function y, the value of ratio Gy over Gx is always negative, therefore the value of derivaive is also always negative. The derivative of the straight line y=f(x)=-x is equal to -1. The derivatives of curves in domain [0 5] are
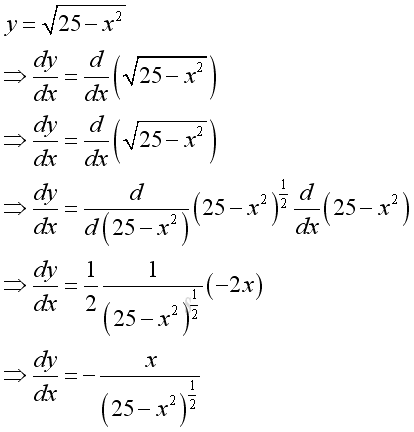 and
and
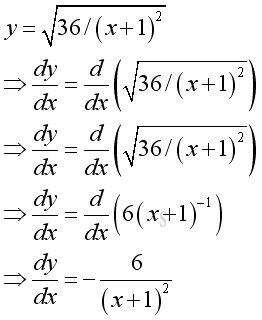
The angles of the tangent line are always greater than π/2, therefore the slopes or their derivatives are always negative.
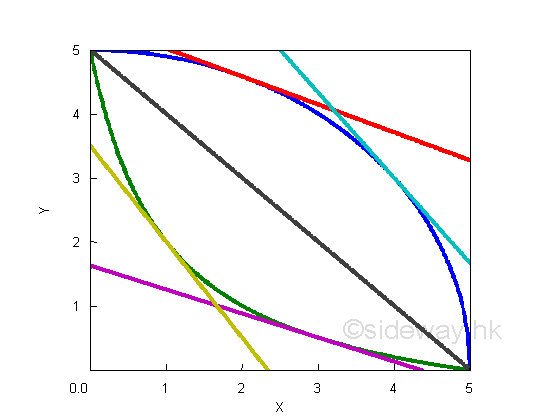
For a constant function y, the value of ratio Gy over Gx is always zero, therefore the value of derivaive is also always zero. Since the constant function is a horizontal line, the tangent line to the curve is a horizontal line also, the slopes or their derivatives are alway equal to zero.
The slopes of curves, derivatives of functions y are:
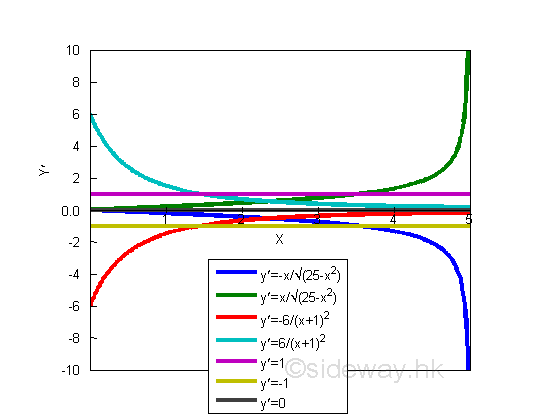
Therefore, the monotonicity can be determined by the sign of derivative.
| Function f(x) in color | Monotonicity of f(x) | sign of dy/dx | Shape of curve dy/dx |
| Green | increasing | + | increasing |
| Magenta | constant | ||
| Cyan | decreasing | ||
| Black | constant | 0 | 0 |
| Blue | decreasing | - | decreasing |
| Yellow | constant | ||
| Orange | increasing |
Concavity
Besides the monotonicity, the concavity of the curve is also important. Similar to monotonicity, the slope of a curve can alway be increasing, i.e. becomes more positive or less negative, remaining constant, or alway be decreasing, i.e. becomes less positive or more negative.
Constant values can also be positive, negative and zero, these values represent the slope of the functions of straight lines. But when considering increasing and decreasing values, they can be described by the concavity.
Therefore, for a positive slope, if the value of slope is getting smaller or not increaseing as x increases, the curve is concave down or concave. And if the value of slope is getting larger or not decreaseing as x increases, the curve is concave up or convex. Similary, for a negative slope, if the value of slope is getting more negative as x increases, the curve is concave up or convex. And if the value of slope is getting less negative as x increases, the curve is concave down or concave.
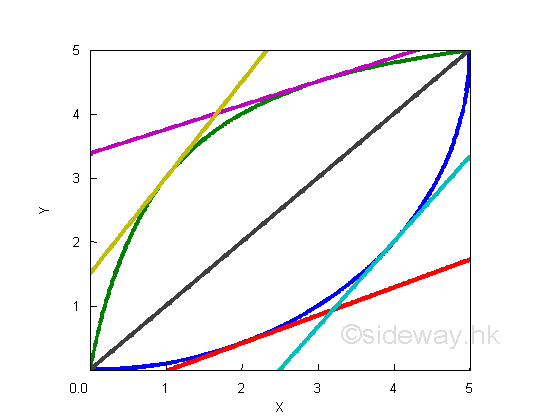
The shape of curves can refereed back to the original function y. And the slope of the slope, or the second derivatives of functions:
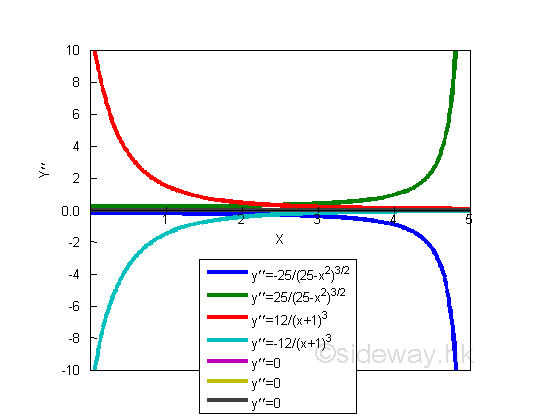
They can be summerized as:
| Function f(x) in color | Monotonicity of f(x) | Sign of dy/dx | Shape of curve dy/dx | Convacity of f(x) | Sign of d2y/dx2 | Shape of curve d2y/dx2 | |
| Green | increasing | + | increasing | convex ∪ | + | increasing | |
| Magenta | constant | line + | 0 | constant | |||
| Cyan | decreasing | concave ∩ | - | increasing | |||
| Black | constant | 0 | 0 | line 0 | 0 | 0 | |
| Blue | decreasing | - | decreasing | concave ∩ | - | decreasing | |
| Yellow | constant | line - | 0 | constant | |||
| Orange | increasing | convex ∪ | + | decreasing |
The second derivatives of a convex, concave up curve is always positive because the slope of curve is always increasing. And the second derivatives of a concave, concave down curve is always negative because the slope of curve is always decreasing.
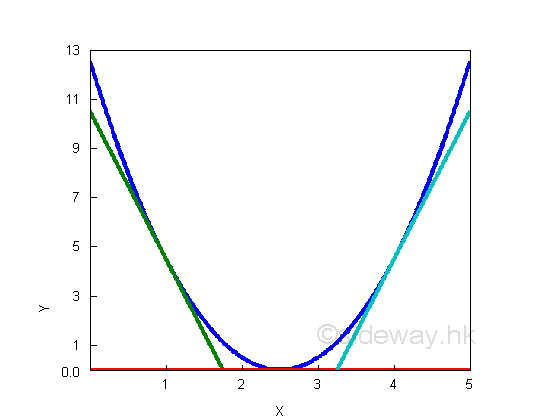
A convex curve, e.g. y=2x2-10x+12.5 increases from negative slope to zero slope, and then to positive slope, the slope or first derivative of the curve is alway increasing and therefore the second derivative of the curve must be positive. The shape of second derivative only provides the rate of change information. imply:
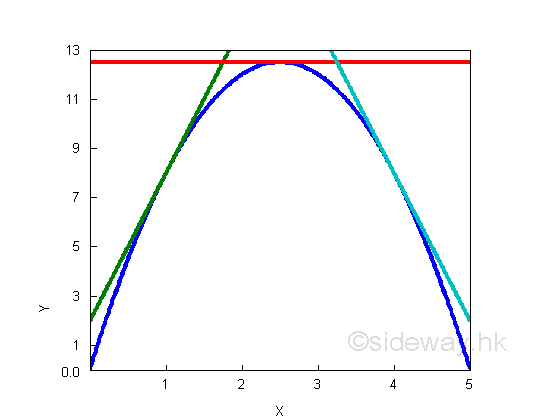
A concave curve, e.g. y=-2x2+10x decreases from positive slope to zero slope, and then to negative slope, the slope or first derivative of the curve is alway decreasing and therefore the second derivative of the curve must be negative. The shape of second derivative only provides the rate of change information. imply:
Local Extreme Values
The combination of two convex curves with negative and positive slopes forms a convex curve with a local or relative minimum. The combination two concave curves with positive and negative slopes forms a concave curve with a local or relative maximum. These values are related values because they are comparing with their neighborhood value, and these values may not be the absolute or global minumum or absolute or global maximum values of the function. For example a damped oscillation, y=5+5e-0.2xcos(5x) in the domain [0,∞), there are infinite number local minima and maxima and there are only one absolute minimum y=0.59 at x=0.628 and one absolute maximum, y=10 at x=0.
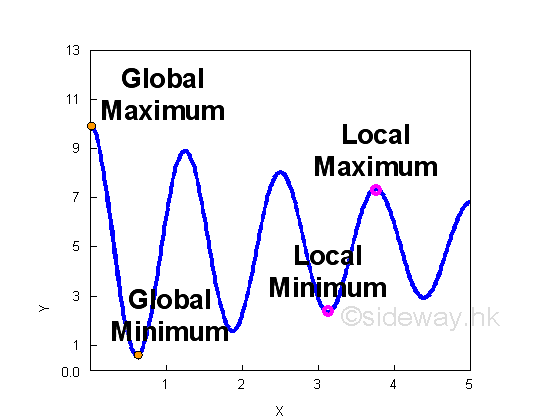
According to the convex and concave curves, the slopes of the curves at both local minimum and local maximum are parallel to the horizontal x axis. The values of derivatives at local minimum and local maximum are equal to zero. Therefore the characteristic of a local minimum and local maximum are the first derivative of the function is equal to zero. However there also exists some functions that the derivatives of these functions at the position of local maximum or local minimum do not equal to zero. Besides, the derivative of a function is equal to zero does not guarantee a local maximum or a local minumum.
The combination of a concave curve with negative slope and a concave curve with positive slope or a convex curve with positive slope and a convex curve with negative slope forms a curve with a sharp point. e.g. y=(x2+7.5x-25)1/2 or 5-(x2+7.5x-25)1/2. And the combination of straight lines with positive slope and negative slope or the combination of straight lines with negative slope and positive slope. e.g. y=|x-2.5| or y=2.5-|x-2.5|.
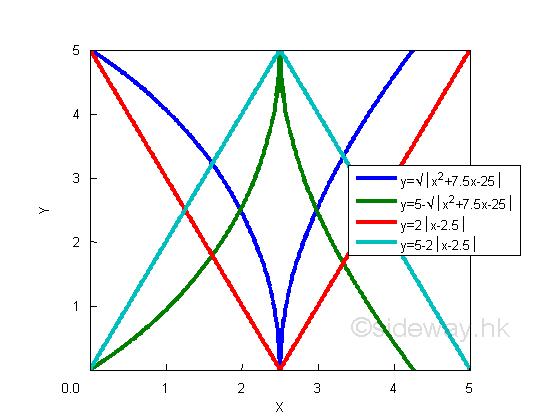
The sharp point formed by two curves with common vertial tangent is call vertial cusp. And the sharp point formed by two curves with no common tangent is call salient point or corner. These function have either local maximum or local minimum position in the curve, but their derivatives at these positions are not equal to zero. The direct calculation of the derivative is undefined at these positions. Although the derivative at these positions does not exist, the left and right derivatives of the functions exist at these positions. As these functions are not differentiable, these functions are not considered.
The combination of a concave curve with positive slope and a convex curve with positive slope or a convex curve with negative slope and a concave curve with negative slope forms a smooth curve with a point of inflexion. e.g y=(x-2.5)3+15 or y=15-(x-2.5)3
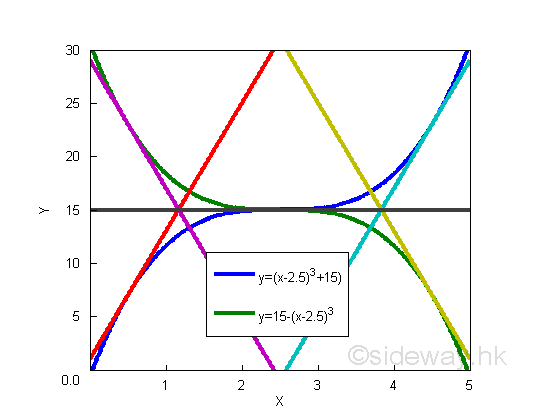
The turning point of the curve is called the point of inflextion. Althrough the derivative at position x=2.5 is equal to zero, the value of the function is neither a local maximum or a local minimum. Therefore the derivative at position equal to zero does not guarantee a local maximum or local minimum at that point. Or functions can have a horizontal tangent at a point that is neither a local maximum nor local minimum at that point. Therefore, in order to confirm whether there is a local maximum or a local minimum at a point, the tangent of its neighborhood points should be checked.
For a local maximum at position x,
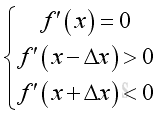
For a local maximum at position x,
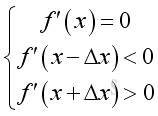
However the tangent of the point of inflexion is also not always equal to zero or parallel to the horizontal axis. e.g. y=5/(1+10-(x-2.5)) or y=5/(1+0.1-(x-2.5)). Or y=x1/3 on real for a point of reflexion with vertical tangent.
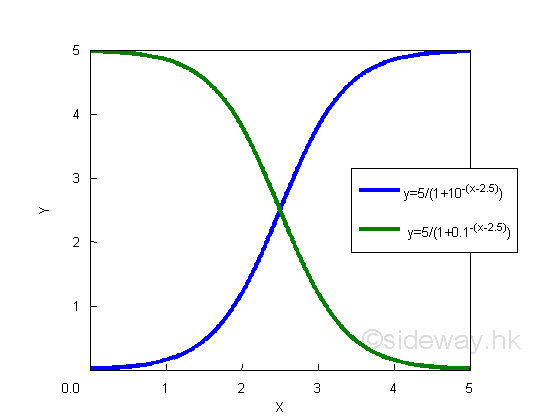
The main difference between point of inflexion and local maximum or local minimum is the combination of curves. Because a curve is constructed by joining a convex curve and a concave curve in either ways, the point of inflexion is always the turning point of curve. The slope of the curve is always either positive slope or negative slope. Since the rate of change of slope of a convex curve is always increasing and the rate of change of slope of a concave is always decreasing, the first derivative of the function or the slope at the point of inflexion is either the local maximum or the local minimum. Therefore the second derivative of the function or the slope of the slope at the point of inflexion should always be equal to zero.

However, a position of function with both the first derivative of the function and the second derivative of the function are equal to zero also can not guartente the position is a point of inflexion also. e.g. y=x4. The position of function with first derivative equals to zero and second derivative equals to zero is a local minumum instead of a point of inflexion.
Therefore, for a point of reflection at position x,
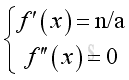
In general, if the graph of function is a concave curve then for a local maximum at position x,
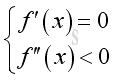
And, if the graph of function is a convex curve then for a local minumum at position x,
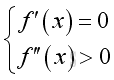
©sideway
ID: 110900026 Last Updated: 10/2/2001 Revision: 0 Ref:
References
- S. James, 1999, Calculus
- B. Joseph, 1978, University Mathematics: A Textbook for Students of Science & Engineering
Latest Updated Links
- Travel Singapore Sight(last updated On 12/6/2025)
- Travel Singapore Rail Network(last updated On 12/5/2025)
- Travel Singapore Things to Know(last updated On 12/4/2025)
- Travel Singapore(last updated On 12/3/2025)
- Legrand Galion(last updated On 12/2/2025)
- Schneider Electric AvatarOn(last updated On 12/1/2025)
- Alfalux(last updated On 11/30/2025)
- Novabell(last updated On 11/29/2025)
- TownGas NJW12RM1(last updated On 11/28/2025)
- SamSung 42" OLED TV S90F 4K(last updated On 11/27/2025)
- Tefal KI7208 GLASS VISION KETTLE(last updated On 11/26/2025)

 Nu Html Checker
Nu Html Checker  53
53  na
na  na
na
Home 5
Business
Management
HBR 3
Information
Recreation
Hobbies 9
Culture
Chinese 1097
English 339
Travel 22
Reference 79
Hardware 54
Computer
Hardware 259
Software
Application 213
Digitization 37
Latex 52
Manim 205
KB 1
Numeric 19
Programming
Web 289
Unicode 504
HTML 66
CSS 65
SVG 46
ASP.NET 270
OS 431
DeskTop 7
Python 72
Knowledge
Mathematics
Formulas 8
Set 1
Logic 1
Algebra 84
Number Theory 206
Trigonometry 31
Geometry 34
Calculus 67
Engineering
Tables 8
Mechanical
Rigid Bodies
Statics 92
Dynamics 37
Fluid 5
Control
Acoustics 19
Natural Sciences
Matter 1
Electric 27
Biology 1
