Content
Limit
of a Function
Limit of Function of Continuous Variable
Limit of Approaching
Limit of a Function
The indexed term of a sequence or series can be considered as the functional value of a function of index n where n can only be positive integer. And the value of index n in the taking limit process for the indexed sequence or series can be any specified large quantity, i.e. n→∞. But for a functional value y=f(x) of a function of x, where x is usually a continuous variable of real number.
Limit of Function of Continuous Variable
In general, the continuous variable x of a function f(x) can be any quantity on the number line. Therefore, the case of the limit of a function, similar to the limit of a sequence of series, is the concern of whether a function y=f(x) has a limit or not when the continuous variable x of the function f(x) increase infinitely, or decrease infiitely, or in both case, i.e. |x|→∞ because a function f(x) can be defined on an interval such that c<x<+∞, or -∞<x<c, or -∞<x<+∞. However the limit of the three cases can be treated similarly because the limit concerns only with the functional value itself not the independent continuous variable. For example, a function f(x) is defined on an interval c<x<+∞, or c>x>-∞, for any specified small quantity ε, there is a large quantity m of the independent continuous variable x, such that |f(m)-A|=ε, and if for all x where |x-m|>0 such that |f(x)-A|<ε, then f(x) has a limit A. Imply
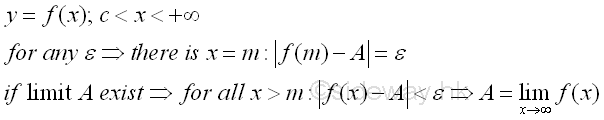
For a function y=f(x), the event of x→∞ can always be represented by an infinite sequence no matter x tending to negative infinity or positive infinity. But for a function of continuous variable, there is infinite continuous functional values corresponding to the independent continous variable. Although infinite terms can be drawn according to the continuous variable to form an infinite sequence, e.g. x1, x2, ..., xi, ..., xn, ..., the formed infinite sequence does not have a limit because there is alway other x greater than the large quantity m to form other infinite sequence infinitely. e.g. x1', x2', ..., xi', ..., xn', .... In order to determine the limit of a function, an infinite sequence is constructed by the dependent continous variable, i.e. the infinite continuous functional values instead of constructing an infinite sequence from the independent continuous variable. That is an infinite continuous sequence f(xn), corresponding to the infinite continuous sequence xn, is used to determine whether the function f(x) approaching a limit or not. Since the independent continuous variable x is continuous, by specifying a small quantity ε, there is always a large quantity m such that |f(m)-A|=ε. If m is sufficiently large then for all x>m such that |f(x)-A|<ε and also valid for all other infinite continuous sequence f(xn'), imply f(x) has a limit A.
For example:
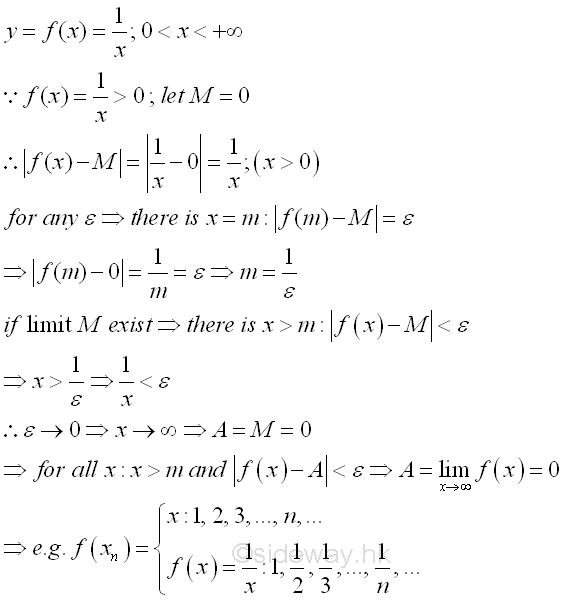
Another typical example of function of continuous variable is the mathematical constant e.
The number e can be defined as the limit of:
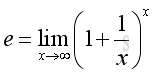
For x tending to +∞, there always exists a pair of integers such that:
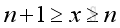
Imply:
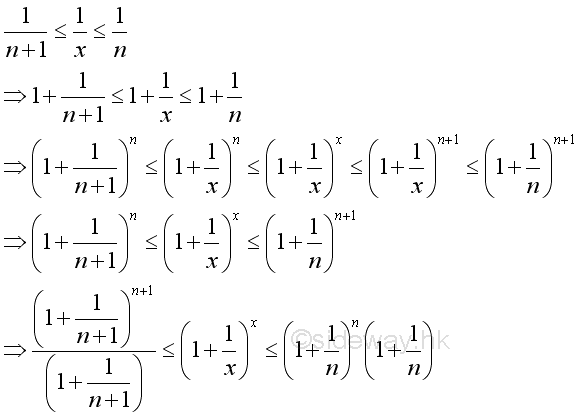
Since the following limits exist and are equal to 1:
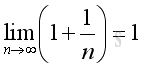 and
and
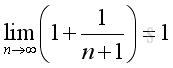
Imply:
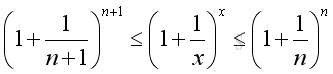
And if limits exist when n tending to +∞, that is:
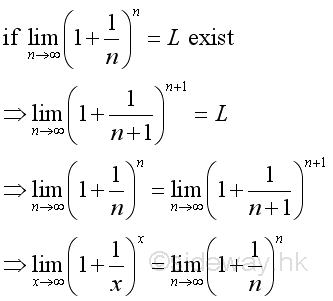
Therefore the limit when x tending to +∞ can be proved by the limit when integer n tending to +∞. And using Binomial Theorem to expand the terms in the bracket of the limit goes up to n, where n tending to +∞:
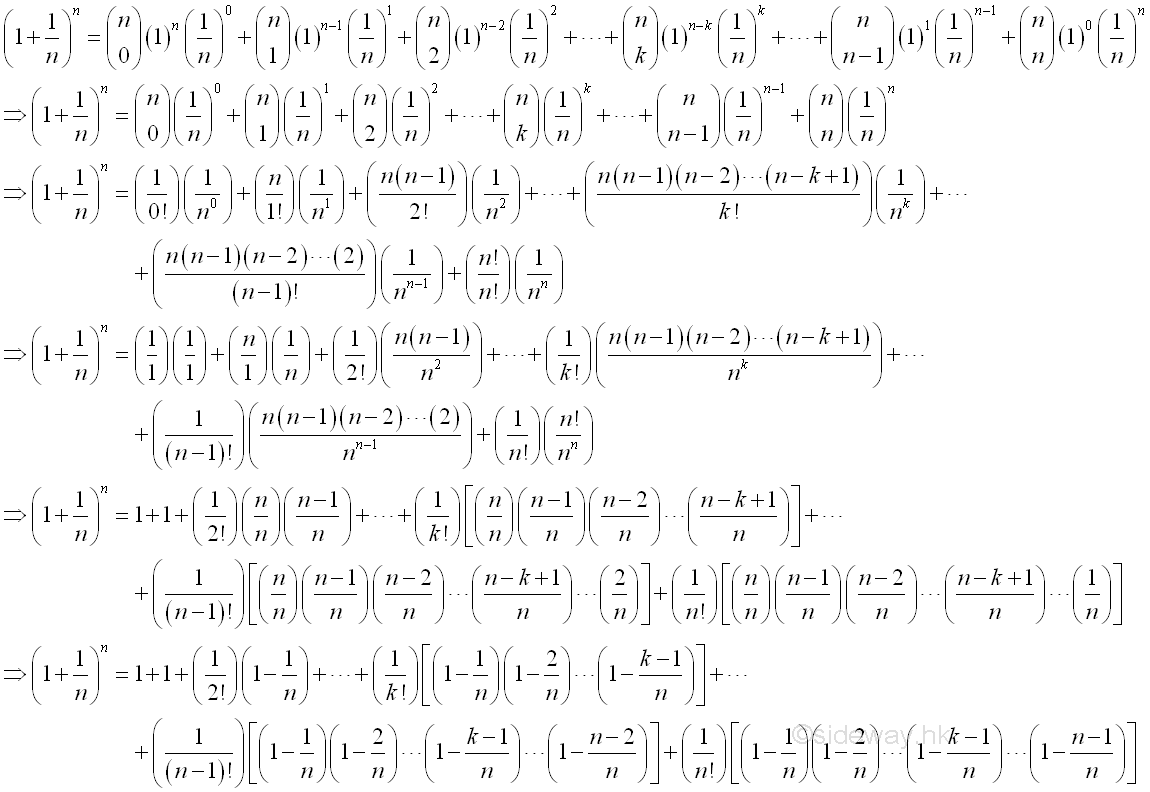
Therefore the limit when n tending to +∞ is:
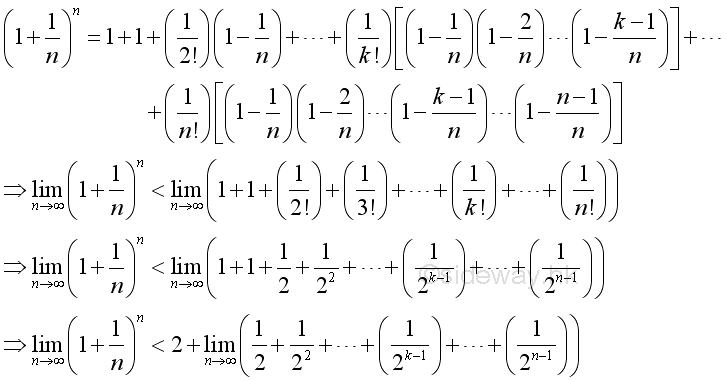
The limit on the RHS when n tending to +∞ is:
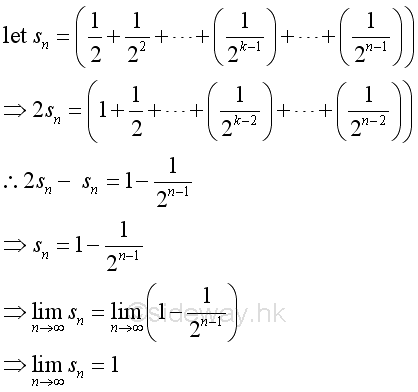
The limit on the LHS when n tending to +∞ exists:
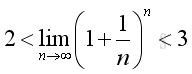
Therefore the limit of the series exists:
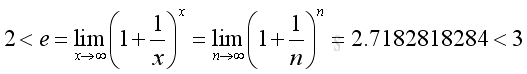
For x tending to -∞, let x=-y then:
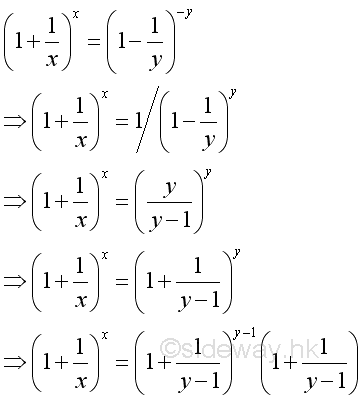
As shown before, when y tending to +∞, imply:
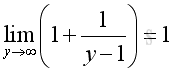 and
and
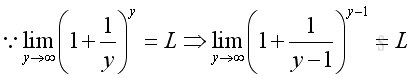
Therefore, when x tending to ∞, imply:
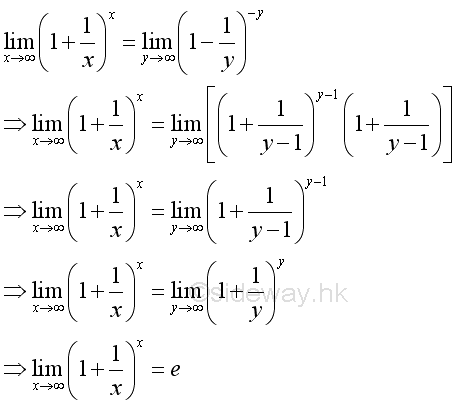
Limit of Approaching
Another case of the limit of a function is the case when an independent variable approaching a number. Unlike the infinite sequence with positive integer index, the functional value of a function can approach the limit continuously as the continuous independent variable tending to infinity continuously. Sometimes a function is also defined on a domain with infinitely continuous numbers in between, therefore the limit of a function does not always refer to the case of an independent variable tending to infinity, the limit of a function can also be the case when an independent variable approaching a number c. Since the numer c can be any number on the domain of x, if c is not the lower or upper limit, the independent variable x can approach from the upper side of the number c to the number c, i.e. x→c+0 or from the upper side of the number c to the number c, i.e. x→c-0. The event of independenct variable unlimited approaching to a number can also be expressed in terms of the closeness to or deviation from a number. In other words, when there is a function f(x) which is defined on the interval a<x<b, the number c of the independenc variable x can be any number on the interval a≤c≤b, then for any small quantity ε, there is a corresponding small quantity δ=|m-c|. such that |f(m)-A|=ε, If δ is sufficiently small, then for all x where |x-c|< δ such that |f(x)-A|<ε, imply f(x) has a limit A at c. Imply
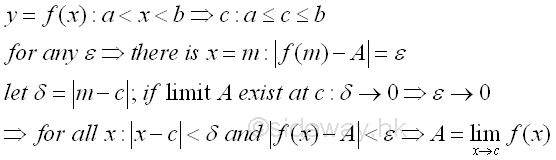
Although the function f(x) is only defined on a<x<b, since the limit of the function at c is observed close to c only in the taking limit process, therefore it is not necessary to care whether the functional value of the function at c is defined or not as in a infinite sequence in taking the limit of a function.
For example:
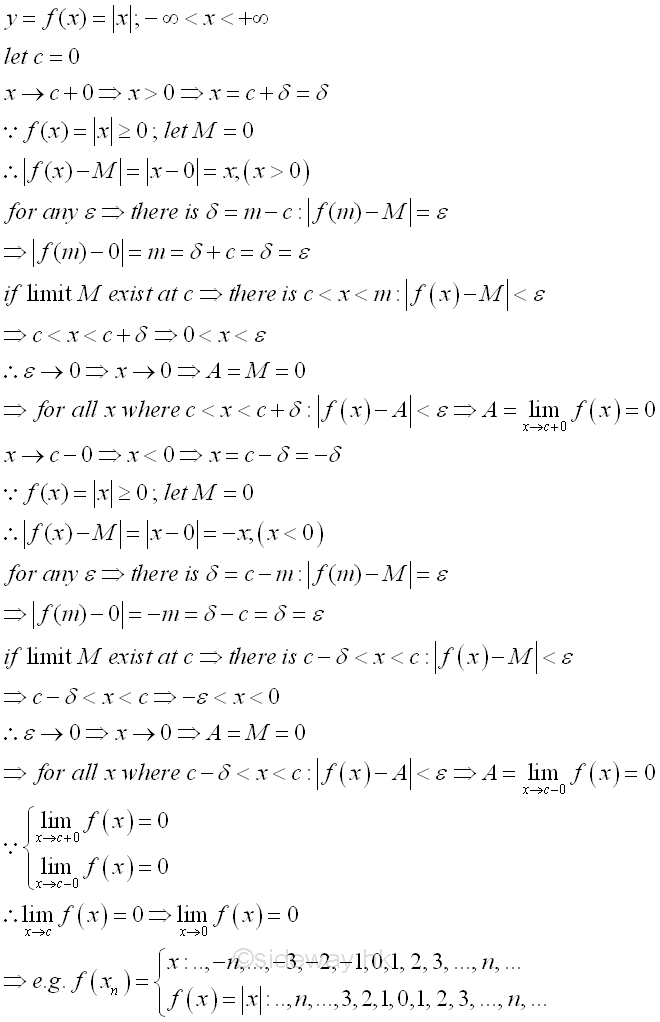
Sometimes the limit exist but the function is undefined at x=c. For example, (sin x)/x
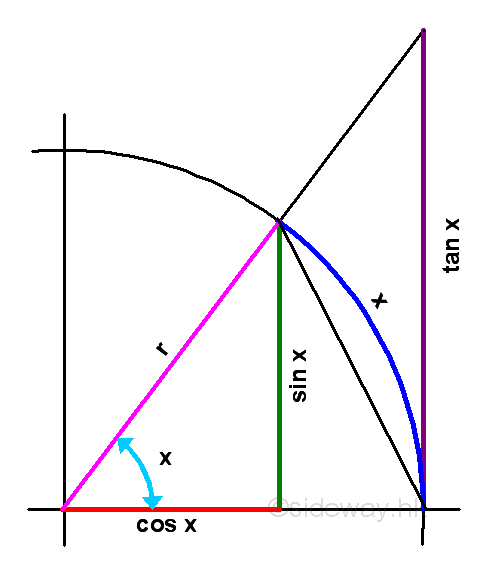
According to the graph, consider the angle x in radian between 0 and π/2 when x approaching zero and not equal to zero, the relationship of the area of triangle with sin x, the area of circular sector with arc x, and the area of triangle with tan x are:
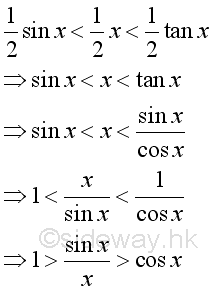
As x decrease, cos x will increase. (sin x)/x will increase also but less than 1. Imply as x approach +0, limit of (sin x)/x exists. Rearrange the inequality:
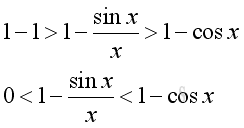
As x approach +0, i.e. δ>x>0 imply:
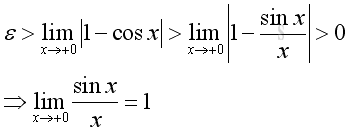
Similarly as x approach -0, imply:
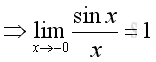
Therefore:
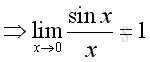
Sometimes the limit does not exist because the two limits of a function tends to two different numbers when approaching a number from both sides. For example,
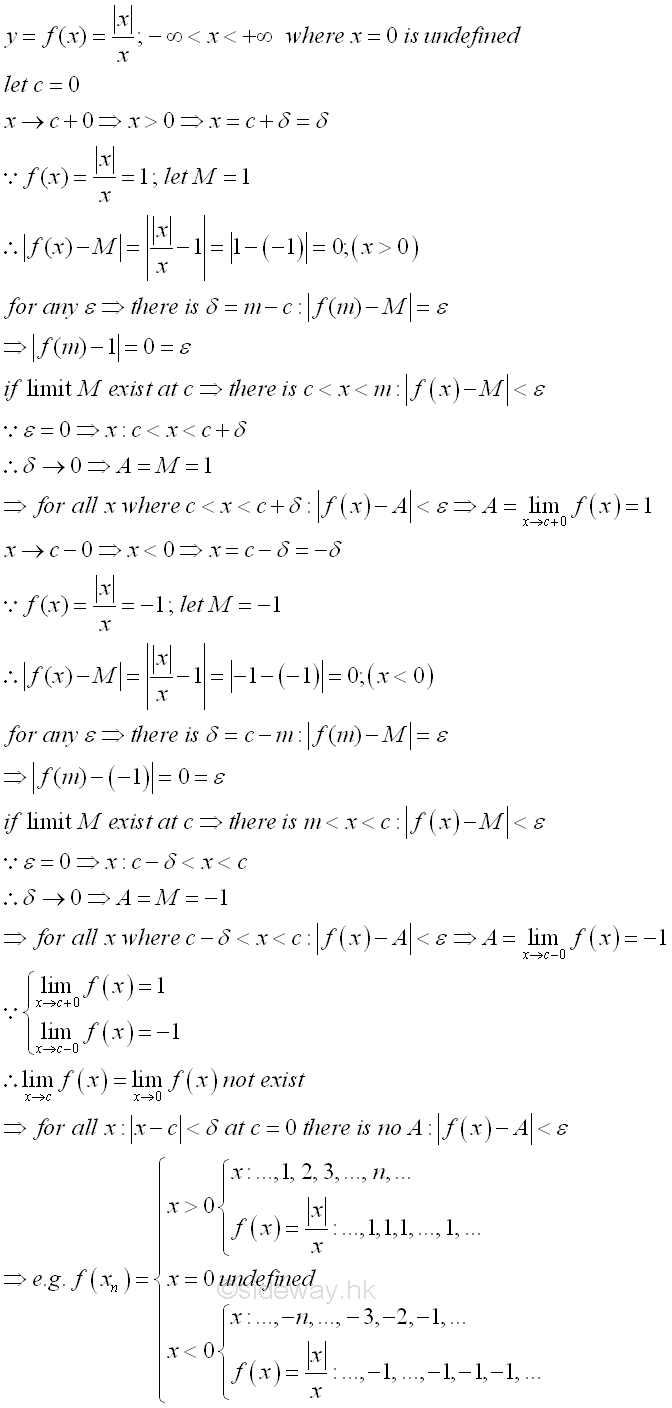
©sideway
ID: 130100003 Last Updated: 1/25/2013 Revision: 0 Ref:
References
- S. James, 1999, Calculus
- B. Joseph, 1978, University Mathematics: A Textbook for Students of Science & Engineering
Latest Updated Links
- Travel Singapore Sight Central(last updated On 1/8/2026)
- Panasonic HHGTQ1001B13 LED Floor Light(last updated On 1/7/2026)
- Travel Singapore Sight West | Central(last updated On 1/6/2026)
- Travel Singapore Sight Sentosa Sensoryscape(last updated On 1/5/2026)
- Travel Singapore Sight Sentosa Resorts World Sentosa(last updated On 1/4/2026)
- Travel Singapore Sight Sentosa HarbourFront(last updated On 1/3/2026)
- Travel Singapore Sight Sentosa(last updated On 1/2/2026)
- Travel Singapore Sight Bird Paradise(last updated On 12/30/2025)
- Travel Singapore Sight Mandai(last updated On 12/30/2025)
- Travel Singapore Sight Singapore Zoo(last updated On 12/30/2025)
- Travel Singapore Sight Rainforest Wild ASIA(last updated On 12/30/2025)

 Nu Html Checker
Nu Html Checker  53
53  na
na  na
na
Home 5
Business
Management
HBR 3
Information
Recreation
Hobbies 9
Culture
Chinese 1097
English 339
Travel 38
Reference 79
Hardware 55
Computer
Hardware 259
Software
Application 213
Digitization 37
Latex 52
Manim 205
KB 1
Numeric 19
Programming
Web 289
Unicode 504
HTML 66
CSS 65
SVG 46
ASP.NET 270
OS 431
DeskTop 7
Python 72
Knowledge
Mathematics
Formulas 8
Set 1
Logic 1
Algebra 84
Number Theory 206
Trigonometry 31
Geometry 34
Calculus 67
Engineering
Tables 8
Mechanical
Rigid Bodies
Statics 92
Dynamics 37
Fluid 5
Control
Acoustics 19
Natural Sciences
Matter 1
Electric 27
Biology 1
