Content
Kinematics: Calculus with Vector Functions for Motion
Limits of Vector Function
Derivative for Vector Function
Rules of
Differentiation for Vector Function
Constant Multiple of Vector Function
Sum of Vector Functions
Product of Scalar Function and Vector Function
Scalar Product of Vector Functions
Vector Product of Vector Functions
Composite Vector Functions
Integral for Vector Function
Kinematics: Calculus with Vector Functions for Motion
Motion in two or three dimension can be described by vector functions of a single variable which can have the common form, r(t)=<f((t),g(t)> for 2D, rr(t)=<f((t),g(t),h(t)> for 3D where f((t),g(t) and h(t) are the componet functions of the vector function. In order to make the vector function make continuous and defined, all component functions should be continuous and defifned within the domain set of variable t of the vector function.
Limits of Vector Function
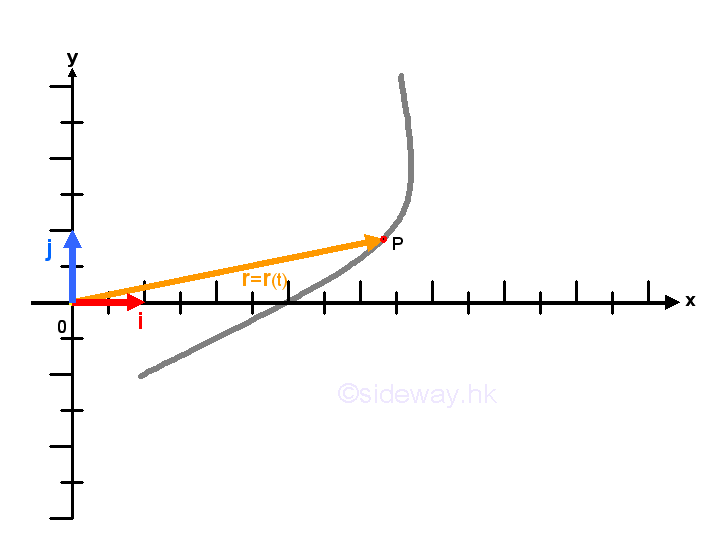
In a general sense, the limit of a vector function is equivalent to the limit of the function of a vector or equal to the limit of all component functions of the vector function. In kinematic 2D or 3D motion, the vector function usually depends on a single real number parameter time, t, that is r(t). And standard unit vectors, i, j, and k, of Cartesian or rectangular three dimensional space with coordinate x,y, and z can also be used to express the vector function as a specific type of vector-valused function such that the vector function can be represented by an algebraic vector expression. Imply

Derivative for Vector Function
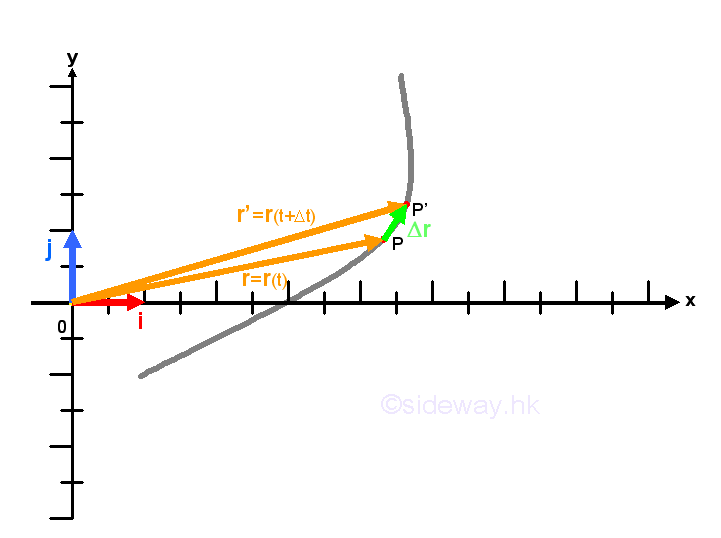
The derivative for vector functions can be derived from the definition of derivative, that is the rate of change of the vector function with respect to independent variable during a infinitely small interval of the independent variable. The change, Δr, of the vector function is equal to the final vector r(t+Δt) minus the initial vector r(t) and is same as the vector joining vector r(t) to vector r(t+Δt) during interval Δt. Geometrically, the change of the vector function due to the small interval can also applied to the component function as in finding limit also. Imply
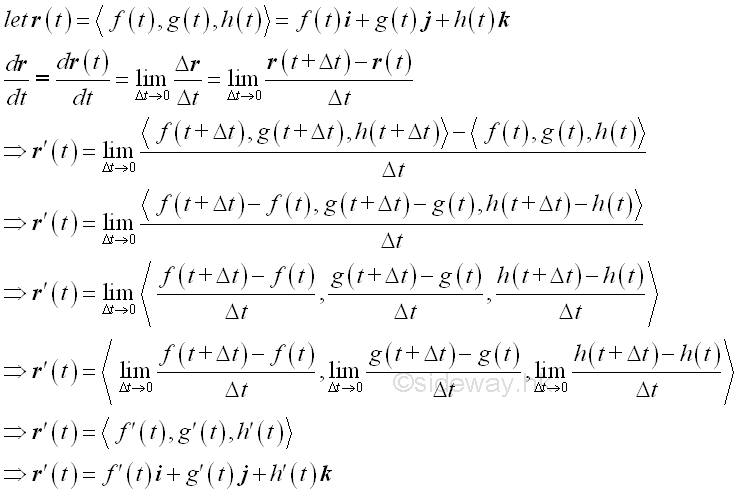
For the expression of a vector-valued function, the form of the derivation of a vector-valued function remains unchange because the functional expression of a unit vector only have a magnitude of a one unit constant along the direction of the coordinate axis and is independent of the independent varible, the derivatives of a unit vector is always equal zero and therefore the derivative of a product of functions remains only the unit vector parts and the derivatives of the unit vector parts are always equal to zero. Imply
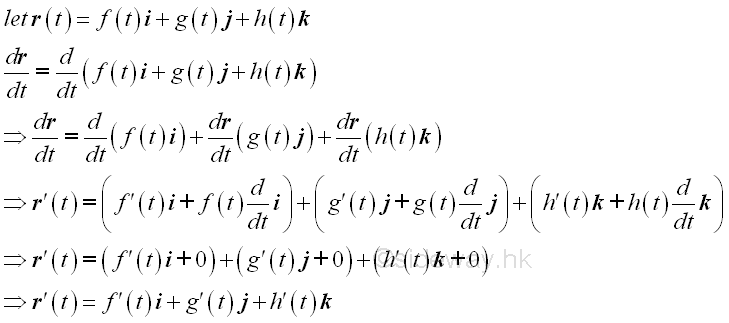
According to the vector-valued function, the change Δr in a vector function can be considered as a fixed ratio of the changes of component functions in term of the indepentent variable t. When the change Δr in a vector function is equal to zero, all changes of component function become zero also. However, when the change Δt of the indepentent variable approaches zero and is sufficiently small, the changes Δr in vector function during the interval Δt can be approximated by a linear function with respect to the independent variable t. In other words, the limiting vector r'(t) or <f'(t),g'(t),h'(t)> is a non-zero vector tangent to the curve with respect to t.
Unlike, the curve representing a function with respect to a independent variable at which the derivative of the function equals to zero which indicates that the function has a horizontal tangent line, the path representing a vector function with respect to a independent variable at which the derivative of the vector function equals to zero means that the changes is equal to zero at a point or direction of change abruptly.
Rules of Differentiation for Vector Function
In general, most standard rules of differentiation can also be extended to vector function.
Constant Multiple of Vector Function
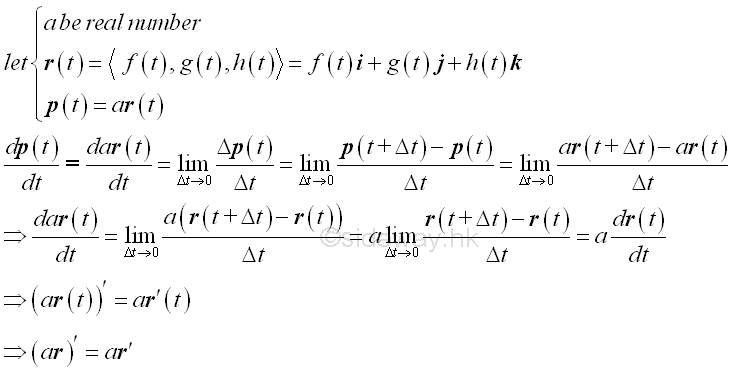
Sum of Vector Functions
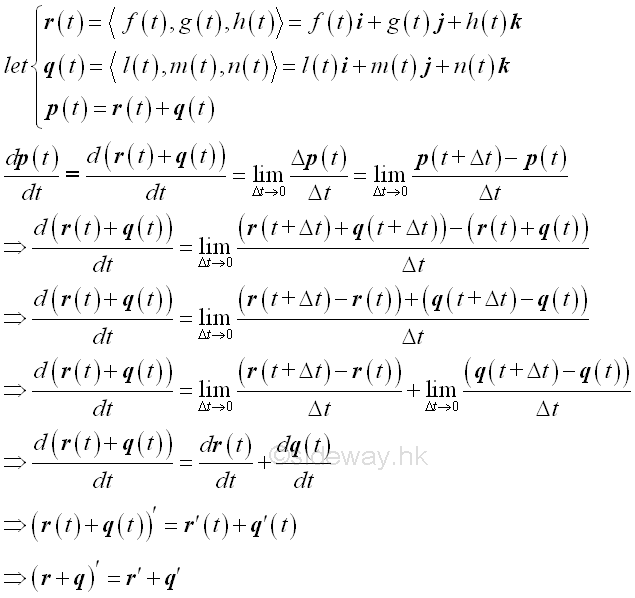
Product of Scalar Function and Vector Function
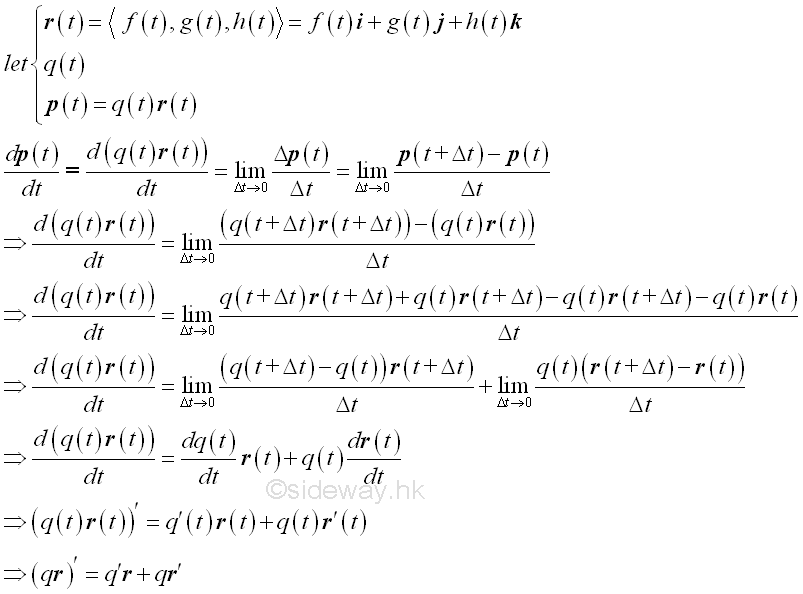
Scalar Product of Vector Functions

Vector Product of Vector Functions
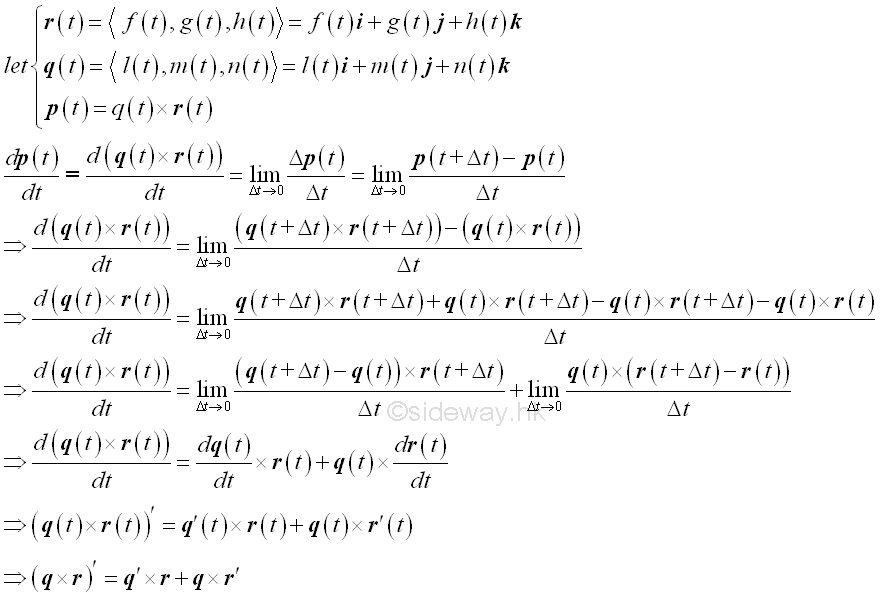
Composite Vector Functions
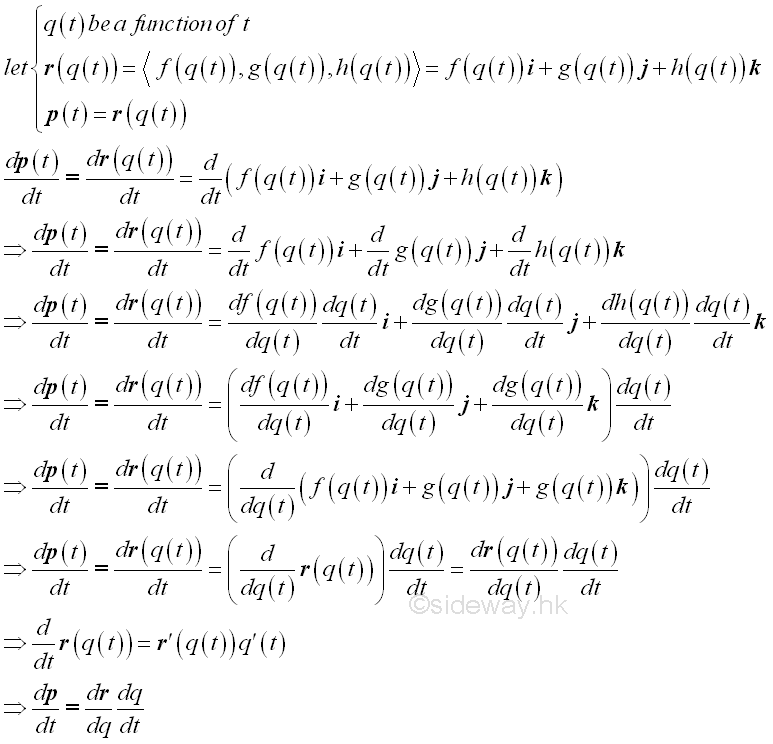
Integral for Vector Function
Since the integral of a function can be considered as the antiderivative of the function, the integral for vector function can be derived similarly.
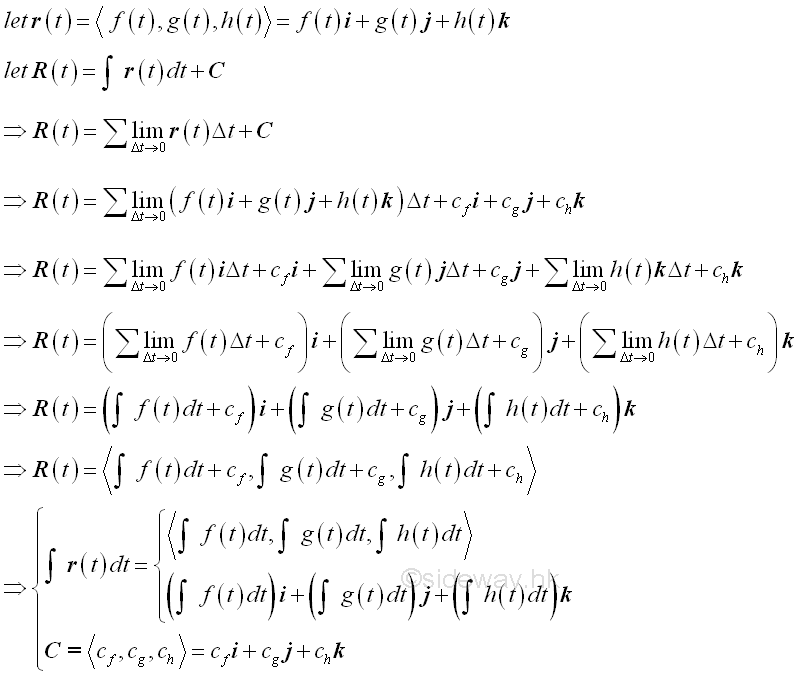
Similarly, the definite integrals are defined as following.
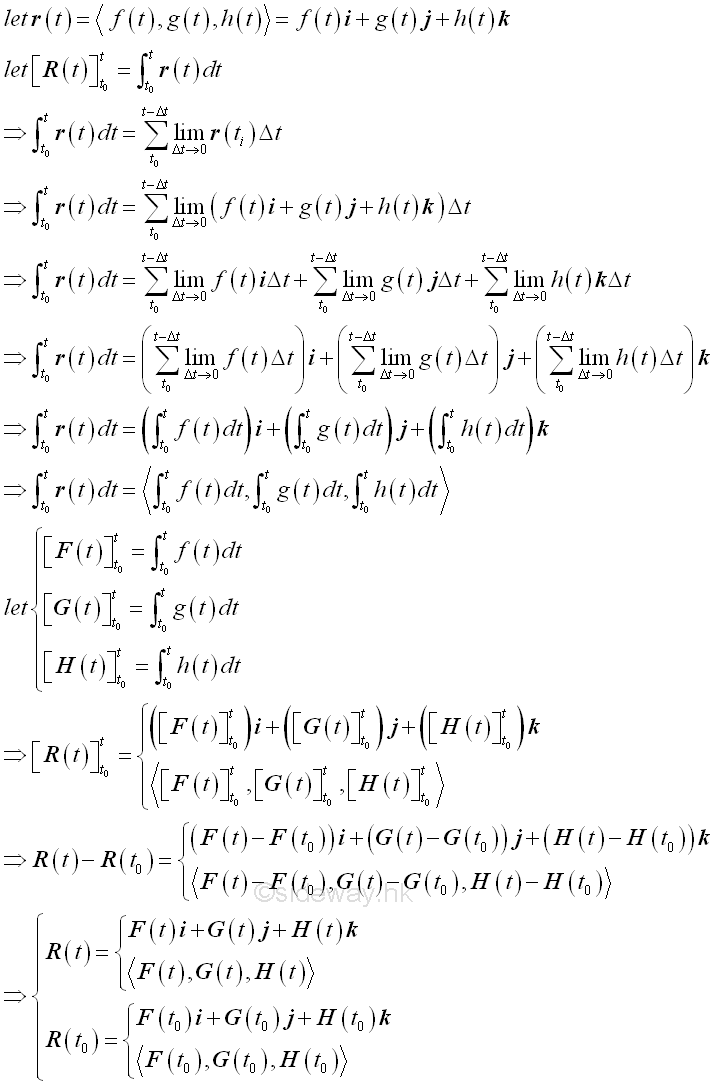
©sideway
ID: 140200019 Last Updated: 3/3/2014 Revision: 1 Ref:
References
- I.C. Jong; B.G. rogers, 1991, Engineering Mechanics: Statics and Dynamics
- F.P. Beer; E.R. Johnston,Jr.; E.R. Eisenberg, 2004, Vector Mechanics for Engineers: Statics
Latest Updated Links
- Travel Singapore Sight Space(last updated On 12/30/2025)
- Travel Singapore Sight Curiosity Cove(last updated On 12/30/2025)
- Travel Singapore Sight Night Safari(last updated On 12/30/2025)
- Travel Singapore Sight River Wonders(last updated On 12/30/2025)
- Travel Singapore Sight Rainforest Wild ASIA(last updated On 12/30/2025)
- Travel Singapore Sight Singapore Zoo(last updated On 12/30/2025)
- Travel Singapore Sight Mandai(last updated On 12/30/2025)
- Travel Singapore Sight Bird Paradise(last updated On 12/30/2025)
- Travel Singapore Sight AltitudeX(last updated On 12/30/2025)
- Travel Singapore Sight(last updated On 12/6/2025)
- Travel Singapore Rail Network(last updated On 12/5/2025)

 Nu Html Checker
Nu Html Checker  53
53  na
na  na
na
Home 5
Business
Management
HBR 3
Information
Recreation
Hobbies 9
Culture
Chinese 1097
English 339
Travel 31
Reference 79
Hardware 54
Computer
Hardware 259
Software
Application 213
Digitization 37
Latex 52
Manim 205
KB 1
Numeric 19
Programming
Web 289
Unicode 504
HTML 66
CSS 65
SVG 46
ASP.NET 270
OS 431
DeskTop 7
Python 72
Knowledge
Mathematics
Formulas 8
Set 1
Logic 1
Algebra 84
Number Theory 206
Trigonometry 31
Geometry 34
Calculus 67
Engineering
Tables 8
Mechanical
Rigid Bodies
Statics 92
Dynamics 37
Fluid 5
Control
Acoustics 19
Natural Sciences
Matter 1
Electric 27
Biology 1
