Content
Kinematics: Rate of Change of a Vector Function
Vector Function of
the Position Function of Motion
Vector Function of
the Velocity Function of Motion
Vector Function of
the Acceleration Function of Motion
Examples of 2D Kinematics:
Projectile Motion
Kinematics: Rate of Change of a Vector Function
A vector function with a single variable, time t can be used to describe the motion of an object in 2 or 3 dimensional space. Because of the properties of the derivative of a vector function, rate of change of component functions of a motion along rectangular coordinate axes, x, y, z, can be determined accordingly.
Vector Function of the Position Function of Motion
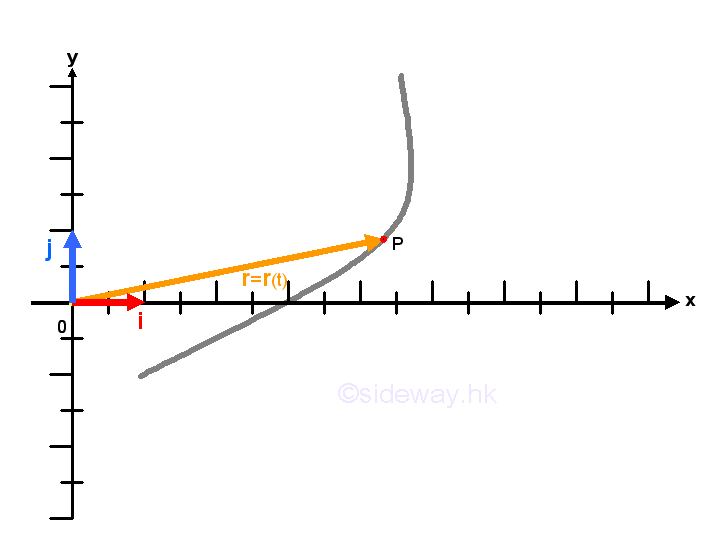
In kinematic 2D or 3D motion, the position P of an object can be expressed in term of a vector function which depends on a single parameter, time t, that is r=r(t). Since a vector function r=r(t) can be resolved into component functions along the rectangular coordinate axes x, y, z, the motion of the object can be described by the position function along the coordinate axes independently.
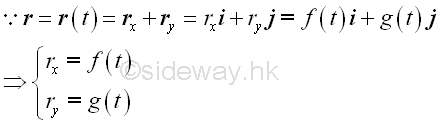
Vector Function of the Velocity Function of Motion
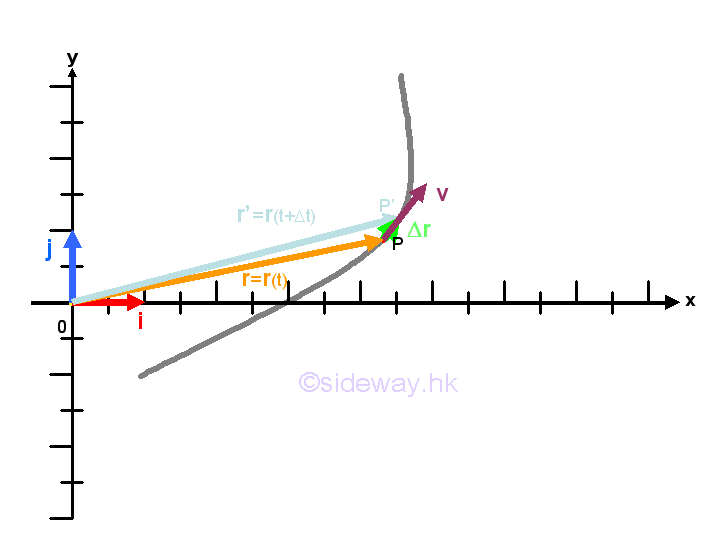
By definition, the rate of change of a vector function of the position function is equal to the velocity function of motion. From the properties of the derivative of vector function, The vector function of velocity functon of motion can be obtained by differentiating the vector function of the position function of motion and a single dot is used to indicate the first derivative of the position function. Imply
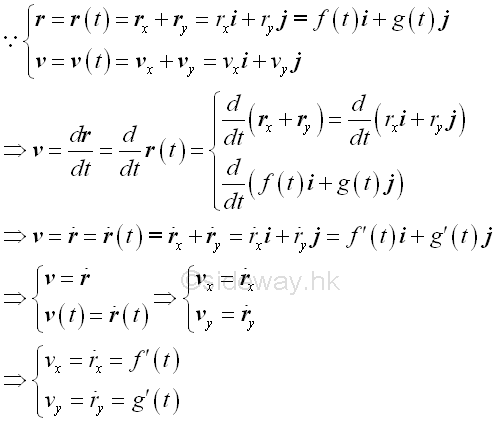
Vector Function of the Acceleration Function of Motion
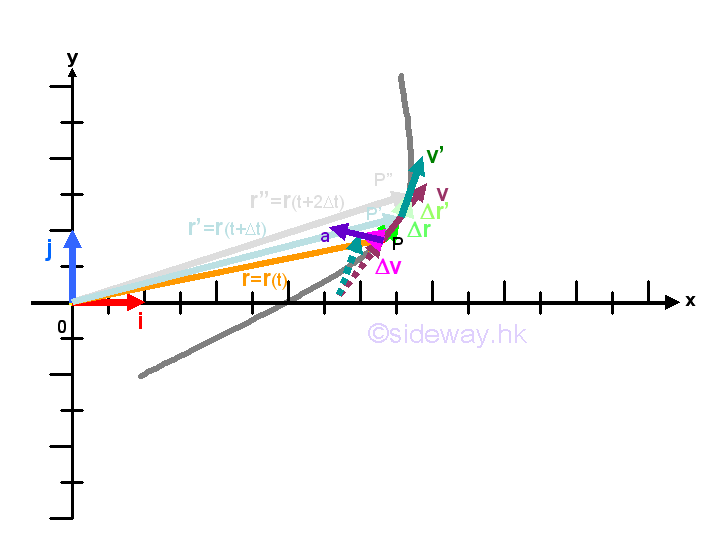
By definition, the rate of change of a vector function of the velocity function is equal to the acceleration function of motion. From the properties of the derivative of vector function, The vector function of acceleration functon of motion can be obtained by differentiating the vector function of the velocity function of motion and a single dot is used to indicate the first derivative of the velocity function. Since a velocity function can be obtained from a position function, therefore a double dot is used to indicate the second derivative of the position function. Imply
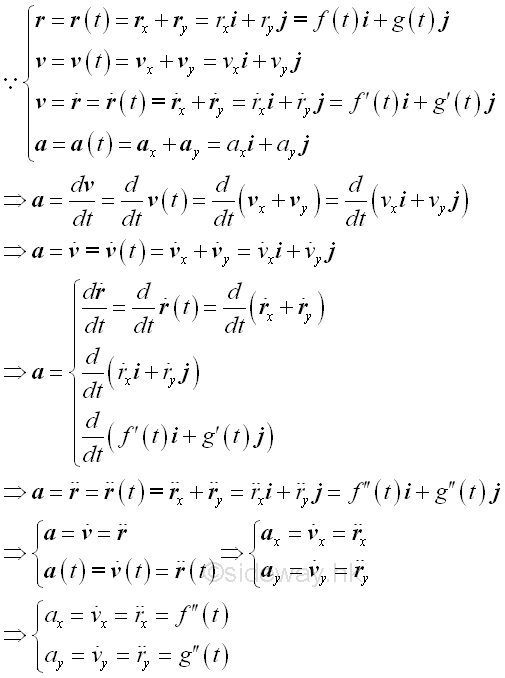
Examples of 2D Kinematics: Projectile Motion
An object is tossed from a h0 m high cliff with initial speed v0m/s at an angle of θ degree. Air resistance may be ignored, so the object is in projectile motion. What is the speed and position of the object after t s before hit the ground? What is the maximum position of the obect and the time required to reach the maximum elevation. And what is the time and the velocity of the object when touching the ground? What is the total horizontal distance of the object travelled?
Assumed the ground of the cliff is the origin O, then let velocity moving upward and rightward is positive. For free projectile, the acceleration of the project can be assumed to be equal to a=9.8m/s2 downward or with negative sense due to gravity where the horizontal acceleration is equal to zero. Both the velocity and position of the object can be expressed as a function in term of time t. At t=t0=0, the given initial velocity is equal to v0 at an angle of c degree and the initial position is equalt to x0. And acceleration is constant and is equal to -g.
Since vertical motion and horizontal motion can be considered independently, the motion of the projectile is treated as two independent linear motions. Therefore the given information of the motion should also be converted into motions along vertical and horizontal axes. Since the origin of the coordinate axes is assumed at the ground of the cliff, at t=t0=0, the horizontal position of the projectile is equal to zero, i.e. x0=0 , while the vertical position of the projectile is equal to h0, i.e. x0=h0. Since the initial velocity is equal to v0m/s at an angle of c degree, at t=t0=0, the horizontal velocity of the projectile is equal to v0cosc , i.e. vx0=v0cosc , while the vertical velocity of the projectile is equal to v0sinc , i.e. vy0=v0sinc . For a free projectile, for all time t, the horizontal acceleration of the projectile is always equal to zero, i.e. ax=0 or a uniform motion, while the vertical acceleration of the projectile is always equal to -g , i.e. ay=-g or a uniform acceleration motion. Since the projectile simultaneously moves vertically in y-direction and horizontally in x-direction with a path of motion, the trajectory the starting and ending time of the mtion must be the same.
The vertical motion

The horizontal motion

The motion of the projectile is

For maximum elevation, the derivation of vertical position function of the projectile is equal to zero, or the vertical velocity of the object is equal to zero. Imply

Since the vertical position of the projectile is equal to zero when hitting the ground, imply

Since the horizonal position of the projectile when hitting the ground is at the same time when the projectile hitting the ground vertically, imply
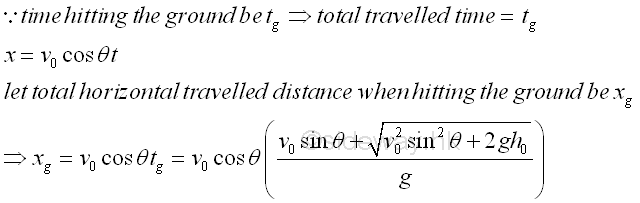
©sideway
ID: 140200020 Last Updated: 3/3/2014 Revision: 1 Ref:
References
- I.C. Jong; B.G. rogers, 1991, Engineering Mechanics: Statics and Dynamics
- F.P. Beer; E.R. Johnston,Jr.; E.R. Eisenberg, 2004, Vector Mechanics for Engineers: Statics
Latest Updated Links
- Travel Singapore Sight Space(last updated On 12/30/2025)
- Travel Singapore Sight Curiosity Cove(last updated On 12/30/2025)
- Travel Singapore Sight Night Safari(last updated On 12/30/2025)
- Travel Singapore Sight River Wonders(last updated On 12/30/2025)
- Travel Singapore Sight Rainforest Wild ASIA(last updated On 12/30/2025)
- Travel Singapore Sight Singapore Zoo(last updated On 12/30/2025)
- Travel Singapore Sight Mandai(last updated On 12/30/2025)
- Travel Singapore Sight Bird Paradise(last updated On 12/30/2025)
- Travel Singapore Sight AltitudeX(last updated On 12/30/2025)
- Travel Singapore Sight(last updated On 12/6/2025)
- Travel Singapore Rail Network(last updated On 12/5/2025)

 Nu Html Checker
Nu Html Checker  53
53  na
na  na
na
Home 5
Business
Management
HBR 3
Information
Recreation
Hobbies 9
Culture
Chinese 1097
English 339
Travel 31
Reference 79
Hardware 54
Computer
Hardware 259
Software
Application 213
Digitization 37
Latex 52
Manim 205
KB 1
Numeric 19
Programming
Web 289
Unicode 504
HTML 66
CSS 65
SVG 46
ASP.NET 270
OS 431
DeskTop 7
Python 72
Knowledge
Mathematics
Formulas 8
Set 1
Logic 1
Algebra 84
Number Theory 206
Trigonometry 31
Geometry 34
Calculus 67
Engineering
Tables 8
Mechanical
Rigid Bodies
Statics 92
Dynamics 37
Fluid 5
Control
Acoustics 19
Natural Sciences
Matter 1
Electric 27
Biology 1
