Content
Product of Matrices
Product of Matrices,
Properties of Matrix Multiplication
Identity Matrix
Inverse Matrix
Product of Matrices
Product of Matrices,
Let
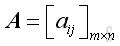 ,
,
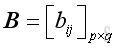 and
and
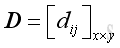 ,
,
for matrix
A
of order m x n,and matrix
B
of order p x q, product of matrices exist if and only if
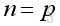 . Then the product of matrices is
. Then the product of matrices is
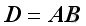 where the order of matrix
D
is x by y and
where the order of matrix
D
is x by y and
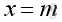 ,
,
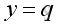 .
The elements of
D are
.
The elements of
D are
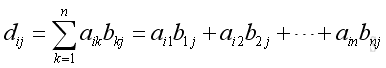
Or
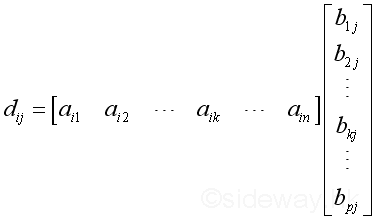
For example,
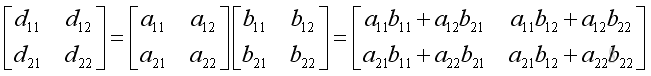
From the definition of matrix multiplication, it is possible to have
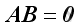 without
without
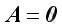 or
or
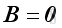 and
and
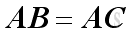 without
without
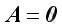 or
or
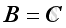 .
.
Properties of Matrix Multiplication
If both matrix B
premultiplied by matrix
A,
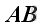 and matrix
B
postmultipled by matrix
A,
and matrix
B
postmultipled by matrix
A,
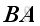 are defined,
are defined,
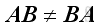 . In general, matrix multiplication is not commutative.
. In general, matrix multiplication is not commutative.
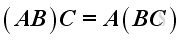 . Multiplication of matrices is associative.
. Multiplication of matrices is associative.
For matrix
A
of order m x n, matrix
B
of order p x q and matrix
C
of order s x t, product of matrices exist if and only if
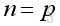 and
and 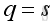 . Then element of
. Then element of
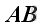 is
is
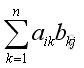
And the element of
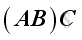 is
is
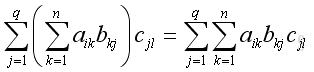
Rearrange the order of terms
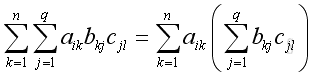
And equals to the element of
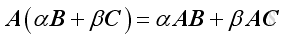 or
or
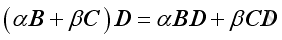 .
.
Matrix multiplication is distributive with respect to addition.
If
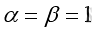 , then
, then
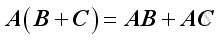 and
and
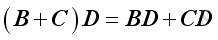 .
.
If A and D are of same order and B and C are square matrices, then A, B, C and D are all square matrices.
Since
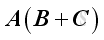 equals
equals
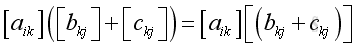 and the element is
and the element is
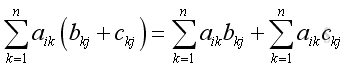
And equals to the element of
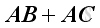 .
.
Identity Matrix
The identity under matrix multiplication is the identity matrix, that is
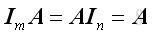
Let
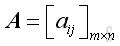 ,
,
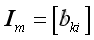 and
and
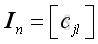 then
then
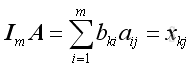
and
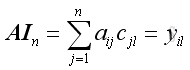
In order to have the same order as A, for element x, order of k should equal to i and for element y, order of l should equal to j, and therefore the identity matrix must be square.
According to the equality of matrices,
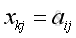 only when
only when
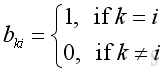 ,
and
,
and
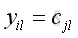 only when
only when
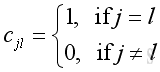 .
.
The form of identity matrix is
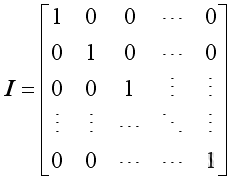 .
.
If
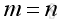 , that is
, that is
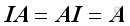 , then
A
must be a square matrix.
, then
A
must be a square matrix.
And therefore it is also called unit matrix.
Inverse Matrix
If A
has an multiplication inverse
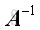 and
and
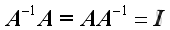 then
A
must be square.
then
A
must be square.
If a matrix has an inverse, the inverse is unique.
Assume both B
and C
are inverses of A,
then
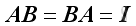 and
and
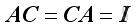 .
.
Premultiply first equation by
C,
imply
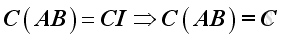 .
.
From second equation, imply
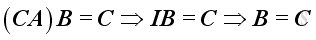 and the inverse is unique.
and the inverse is unique.
Division of matrices has not been defined, the multiplying of the
reciprocal of a matrix can be replaced by multiplying the inverse of the matrix.
Therefore solving
B
in
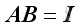 can be obtained by premultiplying
can be obtained by premultiplying
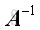 .
.
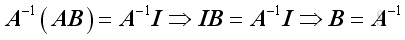
Let
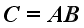 , If both matrices have an inverse, then
, If both matrices have an inverse, then
 . That is
. That is
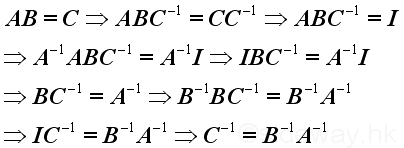
The inverse of a matrix's inverse equals to the matrix itself,
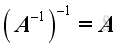 . Let
. Let
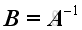 then
then

©sideway
ID: 100800010 Last Updated: 8/14/2010 Revision: 0
Latest Updated Links
- Travel Singapore Sight(last updated On 12/6/2025)
- Travel Singapore Rail Network(last updated On 12/5/2025)
- Travel Singapore Things to Know(last updated On 12/4/2025)
- Travel Singapore(last updated On 12/3/2025)
- Legrand Galion(last updated On 12/2/2025)
- Schneider Electric AvatarOn(last updated On 12/1/2025)
- Alfalux(last updated On 11/30/2025)
- Novabell(last updated On 11/29/2025)
- TownGas NJW12RM1(last updated On 11/28/2025)
- SamSung 42" OLED TV S90F 4K(last updated On 11/27/2025)
- Tefal KI7208 GLASS VISION KETTLE(last updated On 11/26/2025)

 Nu Html Checker
Nu Html Checker  53
53  na
na  na
na
Home 5
Business
Management
HBR 3
Information
Recreation
Hobbies 9
Culture
Chinese 1097
English 339
Travel 22
Reference 79
Hardware 54
Computer
Hardware 259
Software
Application 213
Digitization 37
Latex 52
Manim 205
KB 1
Numeric 19
Programming
Web 289
Unicode 504
HTML 66
CSS 65
SVG 46
ASP.NET 270
OS 431
DeskTop 7
Python 72
Knowledge
Mathematics
Formulas 8
Set 1
Logic 1
Algebra 84
Number Theory 206
Trigonometry 31
Geometry 34
Calculus 67
Engineering
Tables 8
Mechanical
Rigid Bodies
Statics 92
Dynamics 37
Fluid 5
Control
Acoustics 19
Natural Sciences
Matter 1
Electric 27
Biology 1
