Content
Numerical Sequences
Arithmetical Progression (A.P.)[1]
Arithmetic Series[1]
Geometrical Progression (G.P.)[1]
Geometric Series[1]
Numerical Sequences
A numerical sequence is a list of numbers arranged in an order. The numerical sequence itself can be either arranged in a particular order or pattern, or arranged without any order or pattern. The elements of a sequence with n element can be arranged in an ordered sequence of natural numbers with the first element equal to 1, i.e. 1, 2, 3, ..., n-1, n. The elements of a numerical sequence can therefore be represented by an item name with the corresponding item sequence number, i.e. a1, a2, a3, ..., an-1, an. If a numerical sequence is ordered with a pattern, then the elements in the numerical sequence can be expressed in term of the sequence number, n and the term un is usually called a general term of the numerical sequence. For example, the sequence of even natural numbers with sequence number n equal to the number of the element, i.e. a1=2, a2=4, a3=6, ..., an-1=2(n-1), an=2n.

Arithmetical Progression (A.P.)[1]
Arithmetical Progression is a numerical sequence of numbers with the difference between two consecutive numbers is equal to a constant number d called common difference. The numerial sequence is of the form a, a+d, a+2d, a+3d, ... . As the arithmetical progression is a numerical sequence with a pattern, the general term of an arithmetical progression can be expressed in term of the item number, The nth term of an arithmetical progression is an=a1+(n-1)d with the initial term of an arithmetic progression, a1 and the common difference of an arithmetic progression, d. Or in general, an=ai+(n-i)d where ai is the ith term of an arithmetical progression.
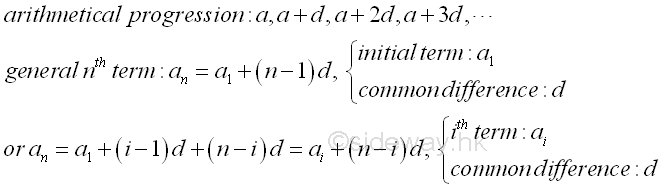
Arithmetic Series[1]
The sum of an arithmetical progression is called arithmetic series. Therefore an
arithmetic series is of the form S=a+(a+d)+(a+2d)+(a+3d)+.... And the general
format of an arithmetic series is Sn=a1+a2+a3+a4+
....+an-1+an =a+(a+d)+(a+2d)+(a+3d)+...+(a+(n-2)d)+(a+(n-1)d) =∑ n
i=1(ai) =∑ n-1
k=0 (a+kd). The sum of an arithmetic series can be determined by the
adding the reverse order of the arithmetic series to the original arithmetic
series, so that
the sum of two arithmetic series can be expressed as the sum of n equal
terms of first term plus last term. And the sum of arithmetic series is
therefore equal to n(2a+(n-1)d)/2. Imply

Geometrical Progression (G.P.)[1]
Geometrical Progression is a numerical sequence of numbers with the difference between two consecutive numbers is equal to a constant multiplier number r called common ratio. The numerial sequence is of the form a, ar, ar2, ar3, ... . As the geometrcal progression is a numerical sequence with a pattern, the general term of a geometrical progression can be expressed in term of the item number, The nth term of a geometrical progression is an=a1rn-1 with the initial term of an geometric progression, a1 and the common ratio of a geometric progression, r. Or in general, an=airn-i where ai is the ith term of a geometrical progression.

Geometric Series[1]
The sum of an
geometrical progression is called geometric series. Therefore an
geometric series is of the form S=a+ar+ar2+ar3+... . And the general format of a geometric series is Snvi8">n=a1+a2+a3+a4+
....+an-1+an =a+ar+ar2+ar3+...+arn-2+arn-1=∑ n
i=1 (ai)=∑ n-1
k=0(ark). The sum of a geometric series can be determined by
multiplying the geometric series by the common ratio r and then deducting the
result from the original geometric series, so that
the difference of two difference geometric series can be expressed as the sum of the
first term of the original geometric series and the last term of the new
geometric series. And the sum of geometric series is
therefore equal to (a(1-rn))/(1-r). Imply
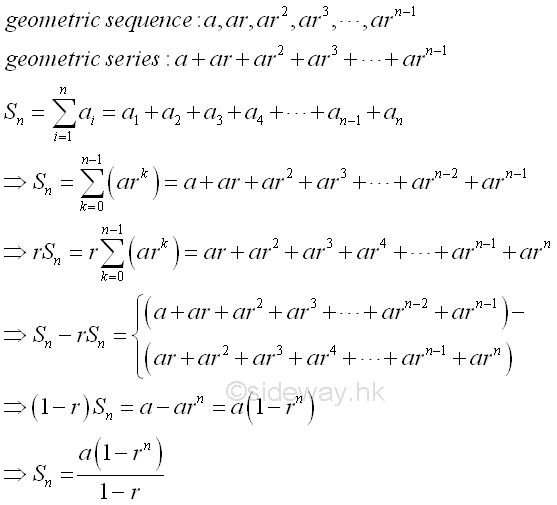
If the numerical value of the common ratio, i.e. |r| or modulus of r, is less than unity, then the sum of the geometric series to infinity can be reduced to Sn=a/(1-r). Imply
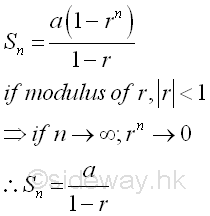
©sideway
ID: 130500018 Last Updated: 5/18/2013 Revision: 0 Ref:
References
- B. Joseph, 1978, University Mathematics: A Textbook for Students of Science & Engineering
- Wheatstone, C., 1854, On the Formation of Powers from Arithmetical Progressions
- Stroud, K.A., 2001, Engineering Mathematics
- Coolidge, J.L., 1949, The Story of The Binomial Theorem
Latest Updated Links
- Panasonic SR-CK05 RiceCooker CW-HZ70AA(last updated On 11/17/2025)
- Panasonic Hood Structure Ventilating Fan Blade Diameter: 8in FV-20WH307 CW-HZ70AA(last updated On 11/16/2025)
- Panasonic Window Mount Thermo Ventilator FV-30BW2H CW-HZ70AA(last updated On 11/15/2025)
- Panasonic Inverter PRO Inverter Window Heatpump Air-Conditioner (3/4 HP) CW-HZ70AA(last updated On 11/14/2025)
- Panasonic Inverter Window-Split Type Cooling Only Air-Conditioner (1 HP) CS-U9YWA(last updated On 11/13/2025)
- Panasonic Inverter Steam and Grill_Microwave Oven 27L NN_DS59NB(last updated On 11/12/2025)
- Panasonic KY-C223B Induction Cooker(last updated On 11/11/2025)
- Focus M41 Single lever kitchen mixer 160(last updated On 11/10/2025)
- Focus Single lever basin mixer 230(last updated On 11/9/2025)
- Precision Start Thermostat shower mixer(last updated On 11/8/2025)
- Tempesta 100 Shower Rail Set 3 sprays(last updated On 11/7/2025)

 Nu Html Checker
Nu Html Checker  53
53  na
na  na
na
Home 5
Business
Management
HBR 3
Information
Recreation
Hobbies 8
Culture
Chinese 1097
English 339
Travel 18
Reference 79
Hardware 40
Computer
Hardware 259
Software
Application 213
Digitization 37
Latex 52
Manim 205
KB 1
Numeric 19
Programming
Web 289
Unicode 504
HTML 66
CSS 65
SVG 46
ASP.NET 270
OS 431
DeskTop 7
Python 72
Knowledge
Mathematics
Formulas 8
Set 1
Logic 1
Algebra 84
Number Theory 206
Trigonometry 31
Geometry 34
Calculus 67
Engineering
Tables 8
Mechanical
Rigid Bodies
Statics 92
Dynamics 37
Fluid 5
Control
Acoustics 19
Natural Sciences
Matter 1
Electric 27
Biology 1
