Content
Centroid of 2D
Plane Body
Centroids of Areas
Area by Integration
Area by Single Integration
Centroid of 2D Plane Body
The centroid of an plate is determined by the first moment of a two dimensional plane body with the method of the first moment of area.
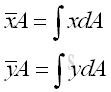
And the centroid of a wire is determined by the first moment of a two dimensional plane body with the method of the first moment of line.
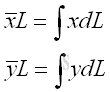
Centroids of Areas
Area by Integration
Although double integration is usually required to determine the planar area. However a planar area can also be determined by performing a single integration. If the inner integration of the unit elemental area is a thin elemental area.
Area by Single Integration
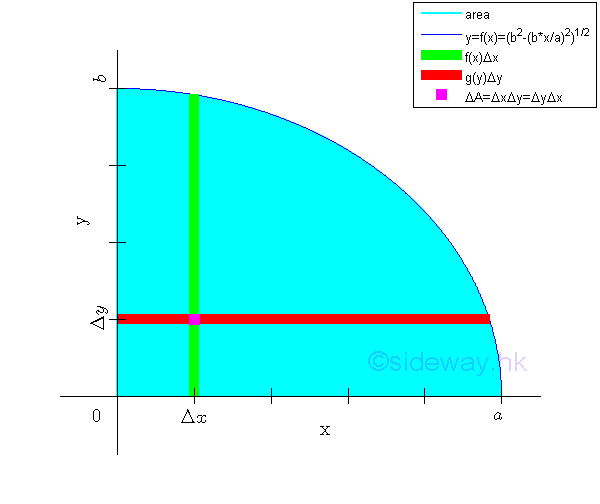
For example, the signed area of the planar region R is bounded by curves in rectangular form , Imply
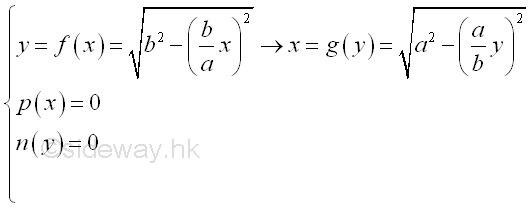
An unit elemental area ΔA in rectangular form can be defined as Δx times Δy. Imply
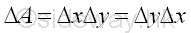
In general, the unit element area of a region can be extended to either a thin vertical rectangular strip or a thin horizontal rectangular strip. And the element area ΔA becomes
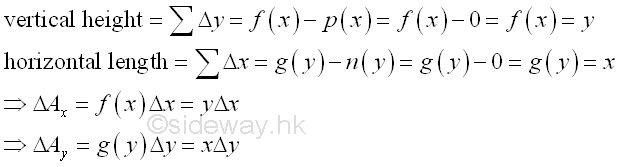
By using a thin rectangular strip as the element area or applying the method of strip slicing, the signed area of the planar region can be determined by a single integration through sweeping the signed elemental area strip along either rectangular coordinate axis. Imply
By sweeping the horizontal strip along y axis vertically
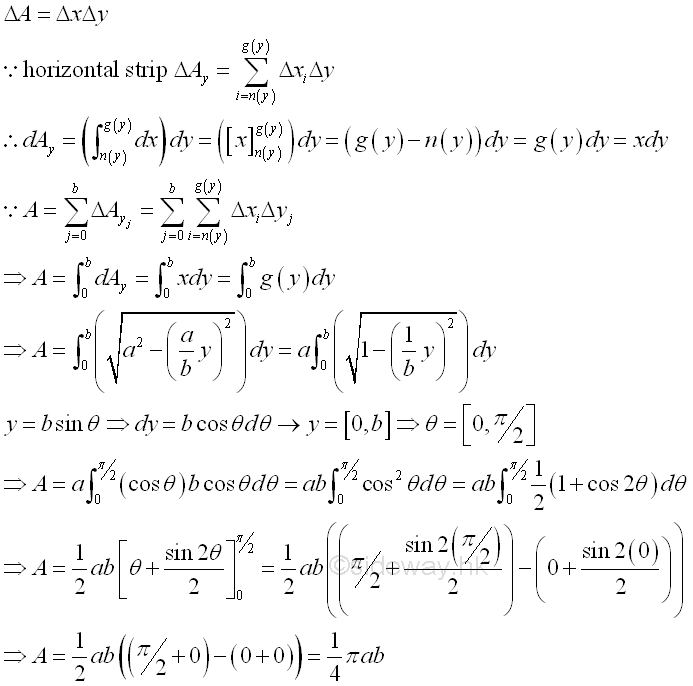
By sweeping the vertical strip along x axis horizontally
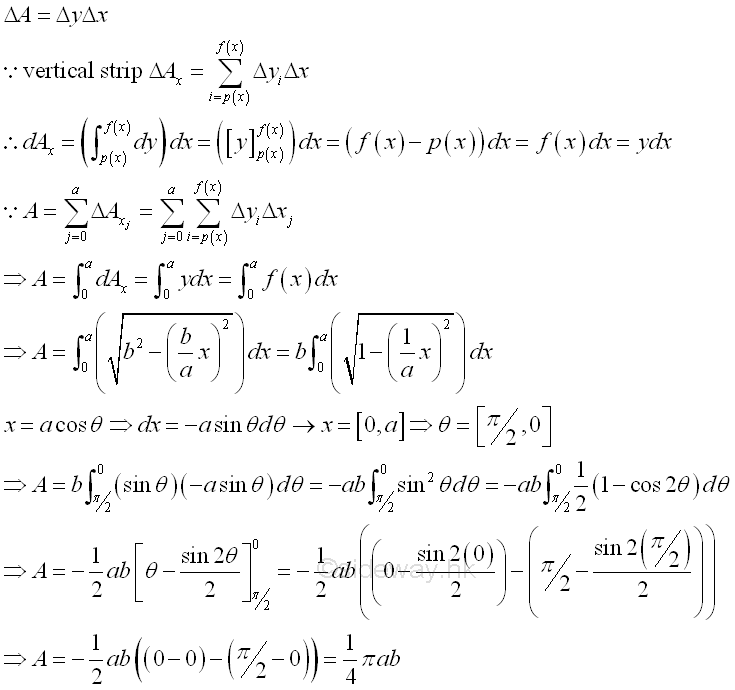
And for curves in polar form
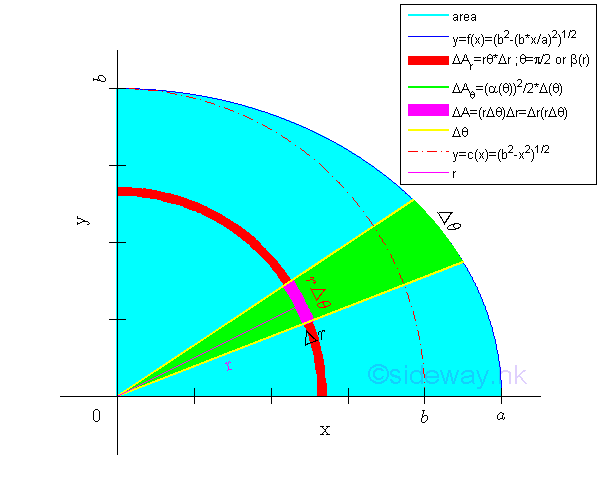
For example, the signed area of the planar region R is bounded by curves in polar form, Imply
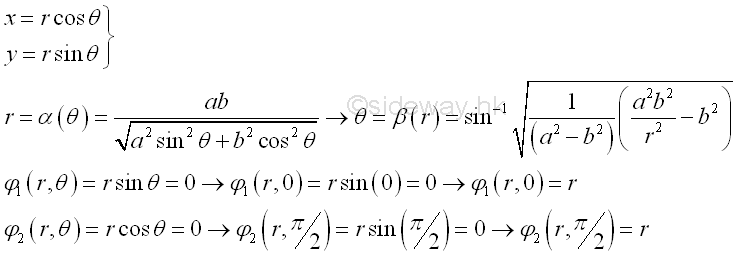
An unit elemental area ΔA in polar form can be approximated by Δr times rΔθ. Imply
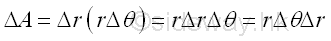
In general, the unit element area of a region can be extended to either a thin slice of circular sector or a thin circular arc strip. And the element area ΔA becomes.
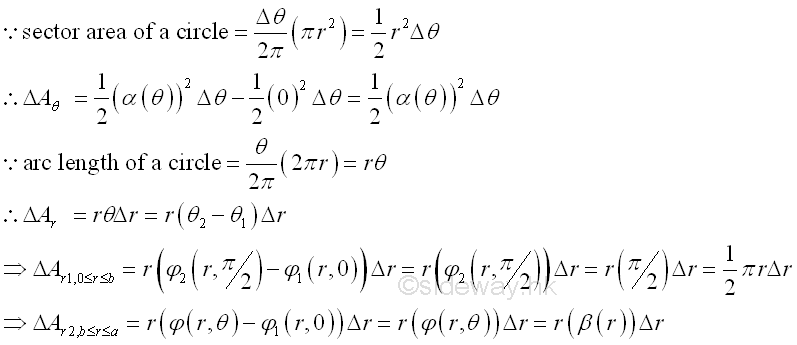
By using a thin circular arc strip as the element area and sweeping radically, or using a thin slice of circular sector as the element area and sweeping circularly, the signed area of the planar region can be determined by a single integration through sweeping the signed elemental area starting from along either polar variables. Imply
By sweeping the thin circular sector slice along variable angle θ circularly
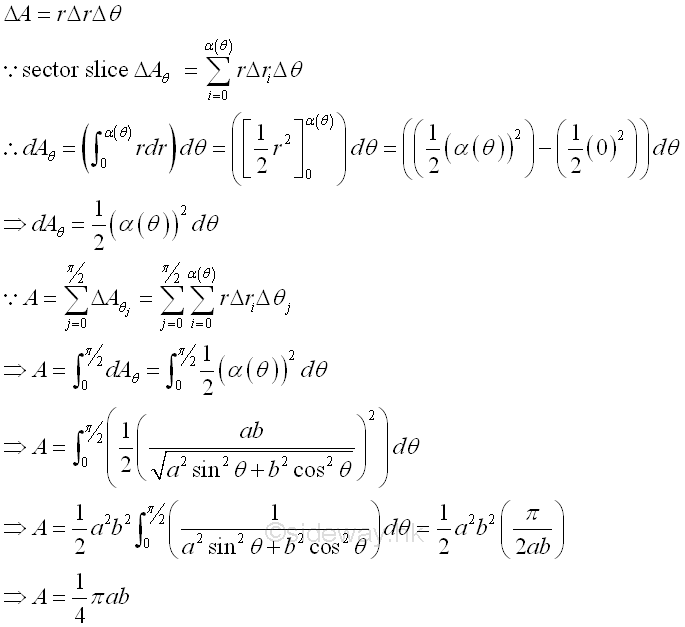
By sweeping the thin circular arc strip along variable radius r radically ,

©sideway
ID: 120600003 Last Updated: 6/2/2012 Revision: 0 Ref:
References
- I.C. Jong; B.G. rogers, 1991, Engineering Mechanics: Statics and Dynamics
- F.P. Beer; E.R. Johnston,Jr.; E.R. Eisenberg, 2004, Vector Mechanics for Engineers: Statics
Latest Updated Links
- Travel Singapore Sight Space(last updated On 12/30/2025)
- Travel Singapore Sight Curiosity Cove(last updated On 12/30/2025)
- Travel Singapore Sight Night Safari(last updated On 12/30/2025)
- Travel Singapore Sight River Wonders(last updated On 12/30/2025)
- Travel Singapore Sight Rainforest Wild ASIA(last updated On 12/30/2025)
- Travel Singapore Sight Singapore Zoo(last updated On 12/30/2025)
- Travel Singapore Sight Mandai(last updated On 12/30/2025)
- Travel Singapore Sight Bird Paradise(last updated On 12/30/2025)
- Travel Singapore Sight AltitudeX(last updated On 12/30/2025)
- Travel Singapore Sight(last updated On 12/6/2025)
- Travel Singapore Rail Network(last updated On 12/5/2025)

 Nu Html Checker
Nu Html Checker  53
53  na
na  na
na
Home 5
Business
Management
HBR 3
Information
Recreation
Hobbies 9
Culture
Chinese 1097
English 339
Travel 31
Reference 79
Hardware 54
Computer
Hardware 259
Software
Application 213
Digitization 37
Latex 52
Manim 205
KB 1
Numeric 19
Programming
Web 289
Unicode 504
HTML 66
CSS 65
SVG 46
ASP.NET 270
OS 431
DeskTop 7
Python 72
Knowledge
Mathematics
Formulas 8
Set 1
Logic 1
Algebra 84
Number Theory 206
Trigonometry 31
Geometry 34
Calculus 67
Engineering
Tables 8
Mechanical
Rigid Bodies
Statics 92
Dynamics 37
Fluid 5
Control
Acoustics 19
Natural Sciences
Matter 1
Electric 27
Biology 1
