Content
Internal Forces
Internal Forces in Members
Straight Two-force Member
Multi-force Member
Two-force Frame Member
Internal Forces
When an rigid body is in static equilibrium, the external forces acting on the rigid body is in equilibrium also. And the members of a static equilibrium structure is in static equilibrium also. When a member is in static equilibrium, the internal forces in the member tending to resist those external forces should be in equilibrium also.
The external forces exert either tension or compression forces on the straight two-force truss member of a truss. There is no moment acting on the member because the line of force acts along the axis of the structure member. The only possible internal forces to react and hold the memeber structure in equilibrium is tension or compression forces also. But when the external forces exert either tension or compression forces on the multiforce truss member of a frame or machine structure, there may have moment acting on the member because the line of force does not alway act along the axis of the structure member or the axis of the sturcture member is not a straight line. These external force usually produce shear forces and bending moments on the structure member and therefore the internal forces to react and hold the member structure in equilbrium is tension or compression forces and together with shear and bending as well.
Internal Forces in Members
Straight Two-force Member
For a straight two-force member, the two external forces at the two end of a truss member should be equal in magnitude and line of action but opposite in sense when the truss member is in equilibrium. The internal forces in truss member can be determined by assuming the member is being cut by an imaginary section plane.
For example a straight two-force member in tension
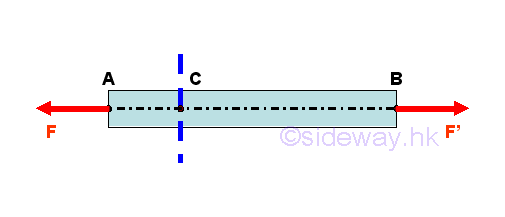
Since the truss member is in equilibrium, tension force F at point A and tension force F' at point B should be equal in magnitude but opposite in sense. For a truss member in equilibrium, the internal forces at the imaginary section plane C should also be in equilibrium. Therefore, the truss member AB can be considered as two separated equilibrium free body models, member section AC and member section CB. Imply
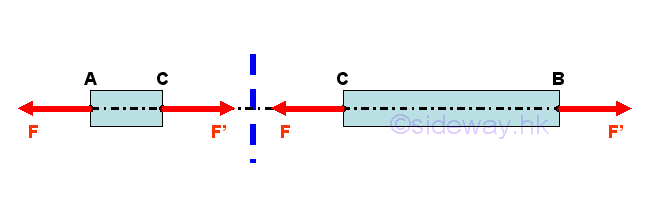
Since the two seperated equilibrium free body models, member section AC and member section CB are in equilibrium, the internal forces reacts by the imaginary section plane C on member section AC and member section CB must equal to external forces on each member. Therefore a force F' which equivalent to the internal force and is equal and opposite to force F should be applied to member section AC at C. And a force F which equivalent to the internal force and is equal and opposite to force F' should be applied to member section CB at C. The internal forces on the two seperated member sections AC and CB should alway exert on each other in truss member AB and are equal in magnitude but opposite in sense. For the straight two-force member, the internal forces are only axial forces along the axis of the straight two-force member, the location of the imaginary section plane C does not affect the magnitude of the internal forces in member AB.
When the straight two-force member in compression
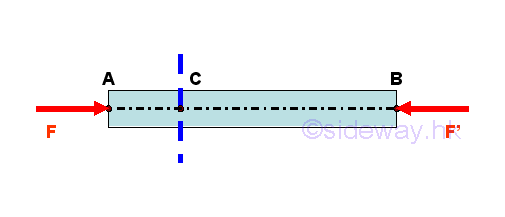
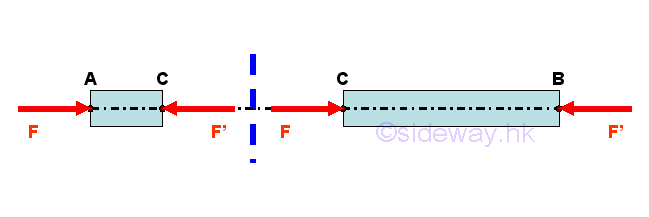
The internal forces can be determined in similar way.
Multi-force Member
For a multi-force member, the external forces acting on the frame member should be equilibrium when the frame member is in equilibrium. The internal forces in frame member can be determined by assuming the member is being cut by an imaginary section plane. For example
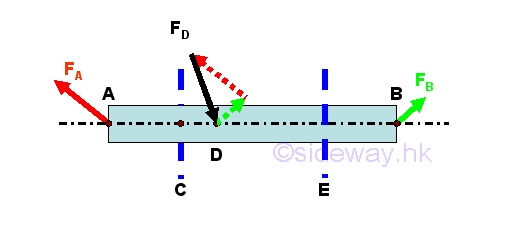
Forces are in equilibrium, imply
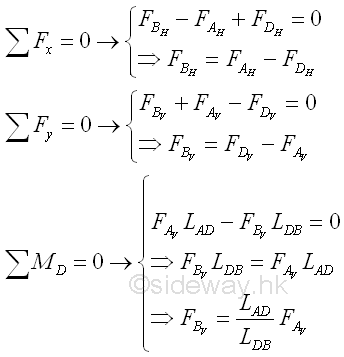
Since the frame member is in equilibrium, The sum of external forces applied to point B and point C should be equal in magnitude but opposite in sense to the external force F at point A. For a frame member in equilibrium, the internal forces at the imaginary section plane C should also be in equilibrium. Therefore, the frame member AB can be considered as two separated equilibrium free body models, member section AC and member section CB. Imply
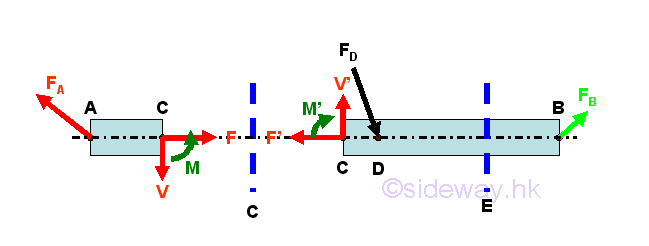
Since the two seperated equilibrium free bodies, member section AC and member section CB are in equilibrium, the internal forces reacts by the imaginary section plane C on member section AC and member section CB must equal to external forces on each member. Therefore a system of forces which equivalent to the internal force and is equal and opposite to force FA should be applied to member section AC at C. And a system of forces which equivalent to the internal force and is equal and opposite to the sum of force FB and FD should be applied to member section CB at C. The internal forces on the two seperated member sections AC and CB should alway exert on each other in truss member AB and are equal in magnitude but opposite in sense. For the straight multi-force member, the internal forces are a system of forces and moment which can be transformed to a force-couple system along the axis of the straight multi-force member, the location of the imaginary section plane C will affect the magnitude of the force-couple system of the internal forces in member AB because the resultant force of the internal forces is affected by the location of application of the external forces and the resultant moment of the internal forces is also affected by the location of interest at which moment of the external forces acting on.
Consider the member section AC of length LAC, the internal forces at point C are
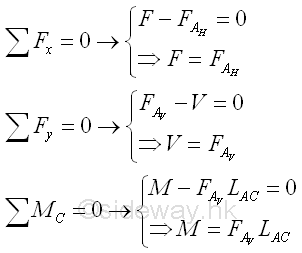
Consider another member section AE of length LAE,
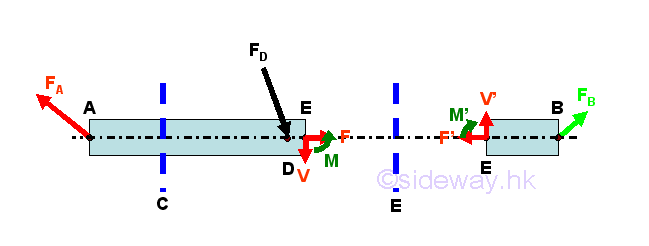
Since the internal forces at the imaginary section plane E should be in equilibrium, the internal forces at point E can also be determined using the member section EB of length LEB, Imply

Therefore the internal forces at point E is not the same the internal forces at point C .
Two-force Frame Member
For a two-force frame member, although the external forces acting on the frame member should be equilibrium when the frame member is in equilibrium, the internal forces in the two-force frame member also varies with the location of the point of interest if the two-force frame member is not a straight member. The internal force of the two-force frame member can also be determined by assuming the member is being cut by an imaginary section plane. For example
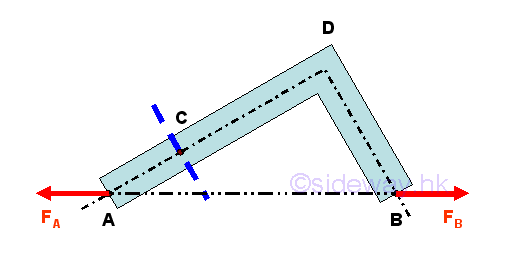
Since the frame member is in equilibrium, tension force F at point A and tension force F' at point B should be equal in magnitude but opposite in sense. For a frame member in equilibrium, the internal forces at the imaginary section plane C should also be in equilibrium. Therefore, the frame member ADB can be considered as two separated equilibrium free body models, member section AC and member section CDB. Imply
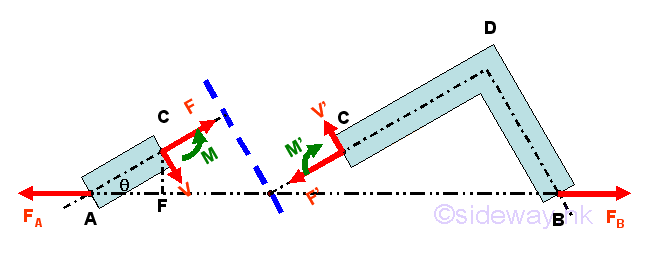
Since the two seperated equilibrium free bodies, member section AC and member section CDB are in equilibrium, the internal forces reacts by the imaginary section plane C on member section AC and member section CDB must equal to external forces on each member. Therefore a system of forces which equivalent to the internal force and is equal and opposite to the system of forces due to force FA should be applied to member section AC at C. And a system of forces which equivalent to the internal force and is equal and opposite to the system of forces due to force FB should be applied to member section CB at C. The internal forces on the two seperated member sections AC and CDB should alway exert on each other in frame member AB and are equal in magnitude but opposite in sense. For the two-force frame member, the internal forces are a system of forces and moment which can be transformed to a force-couple system along the axis of the two-force frame member, the location of the imaginary section plane C will affect the magnitude of the force-couple system of the internal forces in member AB because the resultant moment of the internal forces is affected by the location of interest at which moment of the external forces acting on and the resultant force of the internal forces is also affected by the relative position of application of the external forces.
Consider the frame member section AC of length LAC, the internal forces at point C are
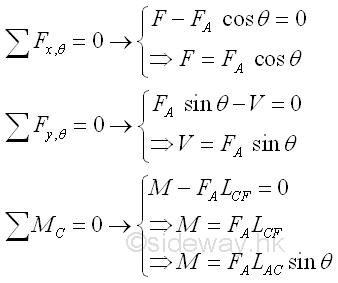
Therefore the internal forces of the frame member section AC varies with the position of interest in the frame member AB.
©sideway
ID: 120800020 Last Updated: 8/22/2012 Revision: 0 Ref:
References
- I.C. Jong; B.G. rogers, 1991, Engineering Mechanics: Statics and Dynamics
- F.P. Beer; E.R. Johnston,Jr.; E.R. Eisenberg, 2004, Vector Mechanics for Engineers: Statics
Latest Updated Links
- Ikea PÅLYCKE clip-on hook rack(last updated On 11/5/2025)
- Ikea SANDSBERG table(last updated On 11/4/2025)
- Ikea TISKEN toilet roll holder(last updated On 11/3/2025)
- Philips CL400 Ceiling Light 36W(last updated On 11/2/2025)
- Philips CL400 Ceiling Light 24W(last updated On 11/1/2025)
- Philips CL400 Ceiling Light 13W(last updated On 10/30/2025)
- Ikea TISKEN basket(last updated On 10/29/2025)
- Ikea TISKEN towel rack(last updated On 10/28/2025)
- Ikea REXBEGONIA mattress protector(last updated On 10/27/2025)
- Ikea KEJSAROLVON mattress protector(last updated On 10/26/2025)
- Ikea KVARNVEN ergonomic pillow(last updated On 10/25/2025)

 Nu Html Checker
Nu Html Checker  53
53  na
na  na
na
Home 5
Business
Management
HBR 3
Information
Recreation
Hobbies 8
Culture
Chinese 1097
English 339
Travel 18
Reference 79
Hardware 28![]()
Computer
Hardware 259
Software
Application 213
Digitization 37
Latex 52
Manim 205
KB 1
Numeric 19
Programming
Web 289
Unicode 504
HTML 66
CSS 65
SVG 46
ASP.NET 270
OS 431
DeskTop 7
Python 72
Knowledge
Mathematics
Formulas 8
Set 1
Logic 1
Algebra 84
Number Theory 206
Trigonometry 31
Geometry 34
Calculus 67
Engineering
Tables 8
Mechanical
Rigid Bodies
Statics 92
Dynamics 37
Fluid 5
Control
Acoustics 19
Natural Sciences
Matter 1
Electric 27
Biology 1
