Content
Law of Conservation
Continuity Equation, 1D
Euler's Equation of Inviscid Motion, 1D
Energy Equation, 1D
Law of Conservation
Based on linear acoustic, assuming the
cross-section area equals to A and no mass is entering or leaving the system due to the acoustic
disturbance, the wave propagation can be represented by following figure:
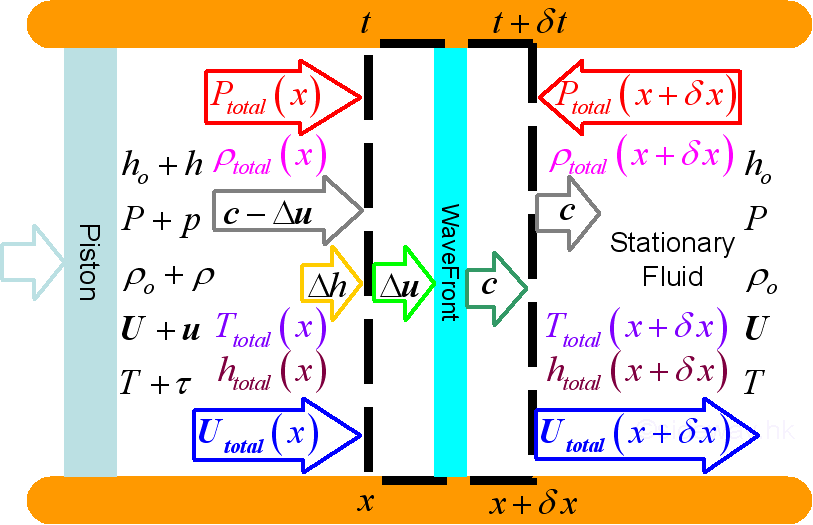
where, at ambient environment and at acoustic disturbance state:
 and,
and,
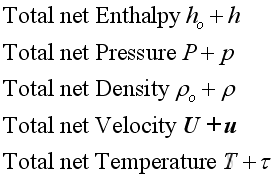
where,
properties of acoustic disturbance:

where,
properties at wavefront:

Continuity Equation, 1D
For a control volume, from the principle of conservation of mass, the instantaneous rate of change of
mass in a control volume equals to the net mass flux flow into or out
of the control volume, therefore:
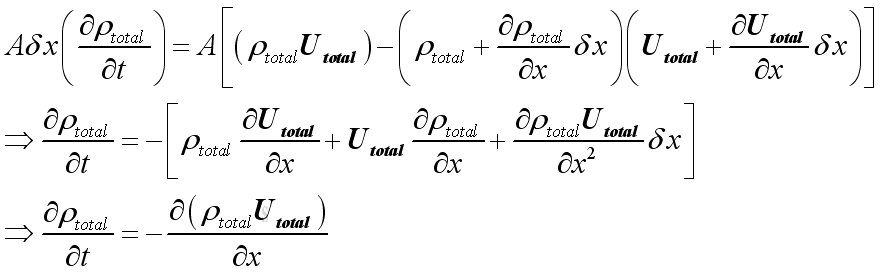
The relationship between density and velocity is defined
Euler's Equation of Inviscid Motion, 1D
For a control volume, from principle of momentum conservation, the
instantaneous rate of change of net momentum of a control
volume equals to the net applied force and the net momentum change due to the
momentum flux flow into or out of the control volume. The applied force in
this case is pressure only and no other forces, no gravity, no viscous force
etc., then:

Since both Utotal , ρtotal are a function of time, imply:
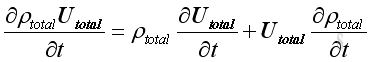
Therefore, because of conservation of mass, the equation is:
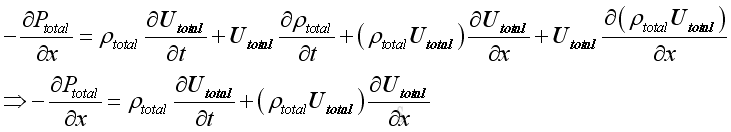
As the medium fluid is assumed to be inviscid, the assumption of inviscid flow is valid for sound propagation and the euler's equation of motion can be applied.
The additional relationship between pressure and velocity is defined
Energy Equation, 1D
For a control volume, from principle of energy conservation, rate of change of
energy equal to rate of heat added and the net rate of energy flow into or out
of the control volume minus the rate of work done. By neglecting heat energy
and external work, and potential energy then:
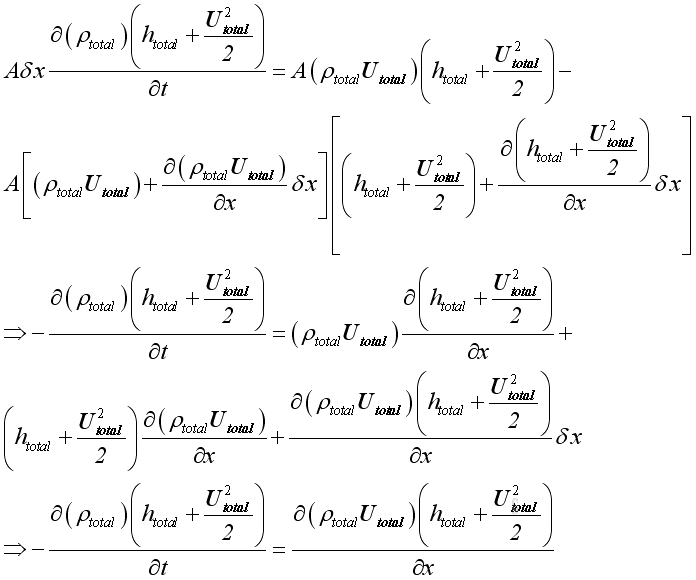
The additional relationship between Enthalpy and velocity is defined.
©sideway
ID: 100900019 Last Updated: 9/17/2010 Revision: 1 Ref:
References
- Michael P. Norton; Denis G. Karczub,, 2003, Fundamentals of Noise and Vibration Analysis for Engieer
- G. Porges, 1977, Applied Acoustics
- Douglas D. Reynolds, 1981, Engineering Principles of Acoustics:; Noise and Vibration Control
- Conrad J. Hemond, 1983, Engineering Acoustics & Noise Control
- F. Fahy, 2001, Foundations of Engineering Acoustics
- D.A. Biew; C.H. Hansen, 1996, Engineering Noise Control: Theory and Practice
Latest Updated Links
- Travel Singapore Sight Sentosa Sensoryscape(last updated On 1/5/2026)
- Travel Singapore Sight Sentosa Resorts World Sentosa(last updated On 1/4/2026)
- Travel Singapore Sight Sentosa HarbourFront(last updated On 1/3/2026)
- Travel Singapore Sight Sentosa(last updated On 1/2/2026)
- Travel Singapore Sight Rainforest Wild ASIA(last updated On 12/30/2025)
- Travel Singapore Sight Bird Paradise(last updated On 12/30/2025)
- Travel Singapore Sight Singapore Zoo(last updated On 12/30/2025)
- Travel Singapore Sight River Wonders(last updated On 12/30/2025)
- Travel Singapore Sight Night Safari(last updated On 12/30/2025)
- Travel Singapore Sight Curiosity Cove(last updated On 12/30/2025)
- Travel Singapore Sight Imbiah(last updated On 12/30/2025)

 Nu Html Checker
Nu Html Checker  53
53  na
na  na
na
Home 5
Business
Management
HBR 3
Information
Recreation
Hobbies 9
Culture
Chinese 1097
English 339
Travel 36
Reference 79
Hardware 54
Computer
Hardware 259
Software
Application 213
Digitization 37
Latex 52
Manim 205
KB 1
Numeric 19
Programming
Web 289
Unicode 504
HTML 66
CSS 65
SVG 46
ASP.NET 270
OS 431
DeskTop 7
Python 72
Knowledge
Mathematics
Formulas 8
Set 1
Logic 1
Algebra 84
Number Theory 206
Trigonometry 31
Geometry 34
Calculus 67
Engineering
Tables 8
Mechanical
Rigid Bodies
Statics 92
Dynamics 37
Fluid 5
Control
Acoustics 19
Natural Sciences
Matter 1
Electric 27
Biology 1
