Content

Acoustic Wave Propagation

Based on linear acoustic, assuming the cross-section area equals to A and no mass is entering or leaving the system due to the acoustic disturbance, the wave propagation can be represented by following figure:

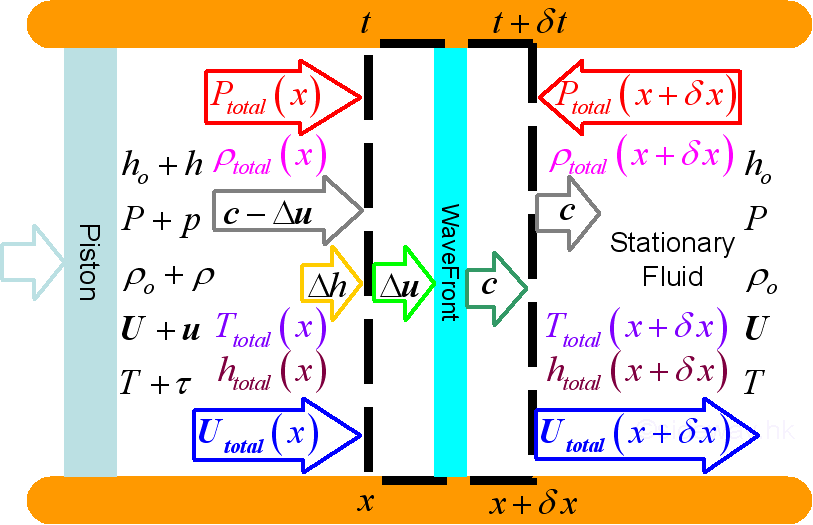
 where, at ambient environment and at acoustic disturbance state:

and,  

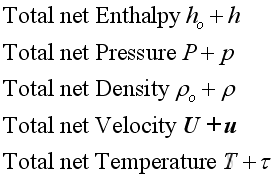
where, properties of acoustic disturbance:

where, properties at wavefront:

Acoustic Propagation Properties

Since the acoustic pressure variations is much smaller than the ambient pressure, the total pressure approximately equals to the ambient pressure.  Similarly, the acoustic density variations is also much smaller than the ambient medium density, the total medium density approximately equals to the ambient medium density. For a quiescent medium, the initial medium velocity equals to zero, therefore the total velocity equals to the acoustic velocity variations.

Besides, for a homogenous quiescent medium, the initial medium velocity, the ambient pressure and the ambient medium density are constant and independent of time and position. Therefore:

Linearized Acoustic Wave Equation, 1D

Since both u , ρ are very small when comparing with ρ_o and they are a function of time and position,  equations can be linearized by neglecting second and higher order  terms.

Substitute.variables approximation into continuity equation and  linearize the equation by neglecting second and higher order  terms, then:

The time derivative of the equation is

Substitute.variable approximations into equation of motion and linearize the equation by neglecting second and higher order  terms, then:

The position derivative of the equation is

Therefore, equate the conservation of mass and conservation of momentum, then:

To simplify the equation, the equation of state is applied and to make the equation more practical, the equation is expressed in term of the fluctuating pressure, which can be measured easily. Then

Speed of Acoustic Wave Propagation

For a control volume, when reducing the control volume to the medium at the wavefront of acoustic wave propagation, from the principle of mass conservation, the mass of medium in the control volume should be constant.

Assume c is the speed of wavefront propagation and propagates away from the source, and Δu is the acoustic velocity fluctuation, since the fluctuation is a relative velocity to the wave propagation, the net medium velocity is c-Δu at the acoustic source side. Then

Alternately, the continuity equation can be expressed as the net instantaneous mass flow into and out of the control volume to be equal. Then

Since c is much greater than Δu, therefore:

Similarly, for the same control volume, from principle of energy conservation, the energy of medium in the control volume should be constant.

Assume  Δh is the acoustic enthalpy variations of the medium in the control volume. Since ρ_totalu_total is not equal to zero and conservation of mass, by neglecting second order small term. Then:

Alternately, the conservation of energy can be expressed as the net instantaneous energy flow into and out of the control volume to be equal. Then

Neglecting second order small term. Then

Equating mass conservation and energy conservation. Then

The acoustic disturbance is small and can be assumed as an isentropic process. Imply

Substitute Δh into the equation of wave propagation, Imply

Since both ρ and p are the small acoustic fluctuation, and under isentropic process, imply

For an isentropic process, imply

Substitute into the equation of wave propagation, Imply

Wave Equation, 1D

Substitute the speed of wave propagation into the wave equation, Imply