Forces
The effect of force on an object can be characterized by its point of application, magnitude, and direction. As force has both magnitude and direction, it is a vector quantity. The unit of force is Newton.
Force Vectors
A force vector can be represented by an arrow with the length of arrow represents the magnitude of the force, the angle between the arrow and the coordinate axis defines the direction of force indicated by the line of action, and the arrow head indicates the sense of direction.
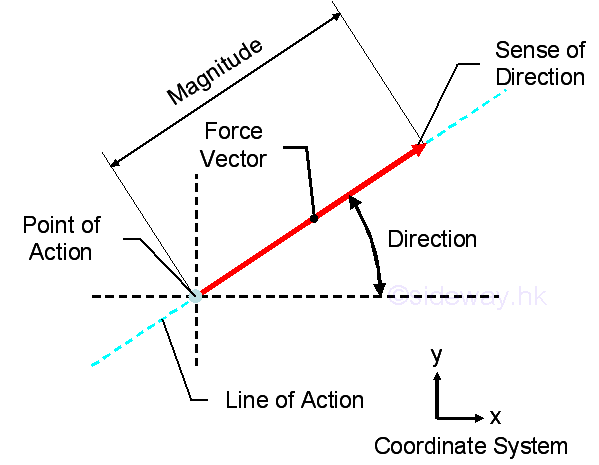
Forces in a Plane
When more than one force act on a point, they can be replaced by a single resultant force with teh same effect on the point of action.
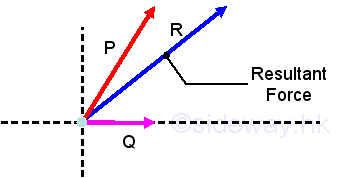
The resultant force can be determined by means of vector addition.
-
Parallelogram Law: The applied forces can be represented by the adjacent sides of the parallelogram and the resultant force can be obtained by drawing the diagonal of the parallelogram.
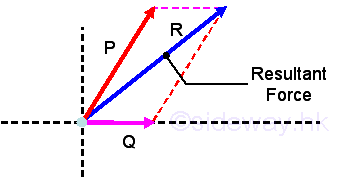
-
Triangle Rule: The applied force can be represented by two sides of a triangle in sequence and the resultant force can be obtained by drawing the third closing side of the triangle.in the opposite sense. Similarly, the triangle rule can further extend to the polygon rule, by using polygon construction method to represent the resultant force in both magnitude and direction.
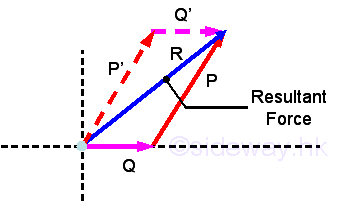
-
Laws of Trigonometric Functions : This is an analytical method based on the geometry instead of using vector construction method with true scale of magnitude and direction.
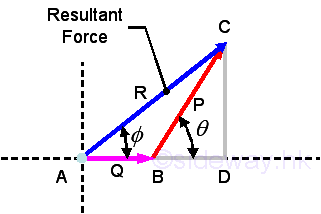
The magnitude of the resultant froce can be determined by pythagorean theorem or the law of cosines.
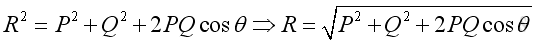
The direction of the resultant froce can be determined by the law of sines.
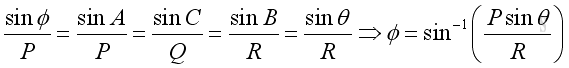
or be determined by the triangle rules.
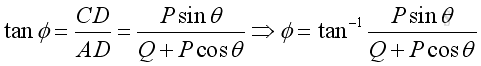
Force decomposition
From the parallelogram Law, force can be resolved into two components. When the two components are perpendicular to each other in the form of a rectangle, they are called rectangular components.
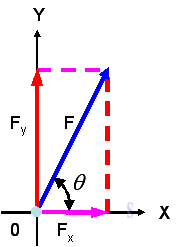 or
or
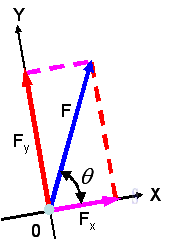
Assumed two unit vectors, i and j, with unit magnitude along the x and y axis. Then
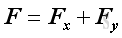 ,
,
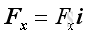 , and
, and
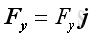 , imply
, imply
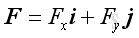
The two components of the force vector can be obtained by
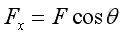 and
and
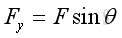
The magnitude of the force vector can also be obtained by
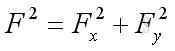
And the direction of the force vector can also be obtained by
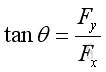
Force Equilibrium
According to Newton's first law of motion, when a particle is in equilibrium, the resultant of all the forces acting on it is zero. That is
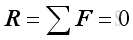
And graphically in the form of force polygon,
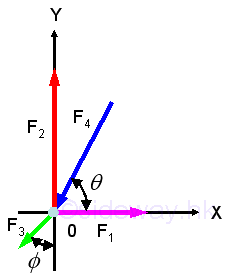 , imply
, imply
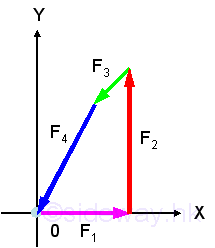
When there are only three applied forces, the problem can be reduced to a force triangle and be solved by trigonometry.
Analytically, forces can be resolved into rectangular components to form the equations of equilibrium. Imply
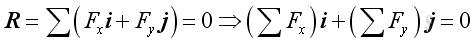
Therefore,
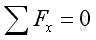 and
and
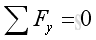
©sideway
ID: 110400006 Last Updated: 4/30/2011 Revision: 0 Ref:
References
- I.C. Jong; B.G. rogers, 1991, Engineering Mechanics: Statics and Dynamics
- F.P. Beer; E.R. Johnston,Jr.; E.R. Eisenberg, 2004, Vector Mechanics for Engineers: Statics
Latest Updated Links
- Travel Singapore Sight Central(last updated On 1/8/2026)
- Panasonic HHGTQ1001B13 LED Floor Light(last updated On 1/7/2026)
- Travel Singapore Sight West | Central(last updated On 1/6/2026)
- Travel Singapore Sight Sentosa Sensoryscape(last updated On 1/5/2026)
- Travel Singapore Sight Sentosa Resorts World Sentosa(last updated On 1/4/2026)
- Travel Singapore Sight Sentosa HarbourFront(last updated On 1/3/2026)
- Travel Singapore Sight Sentosa(last updated On 1/2/2026)
- Travel Singapore Sight Bird Paradise(last updated On 12/30/2025)
- Travel Singapore Sight Mandai(last updated On 12/30/2025)
- Travel Singapore Sight Singapore Zoo(last updated On 12/30/2025)
- Travel Singapore Sight Rainforest Wild ASIA(last updated On 12/30/2025)

 Nu Html Checker
Nu Html Checker  53
53  na
na  na
na
Home 5
Business
Management
HBR 3
Information
Recreation
Hobbies 9
Culture
Chinese 1097
English 339
Travel 38
Reference 79
Hardware 55
Computer
Hardware 259
Software
Application 213
Digitization 37
Latex 52
Manim 205
KB 1
Numeric 19
Programming
Web 289
Unicode 504
HTML 66
CSS 65
SVG 46
ASP.NET 270
OS 431
DeskTop 7
Python 72
Knowledge
Mathematics
Formulas 8
Set 1
Logic 1
Algebra 84
Number Theory 206
Trigonometry 31
Geometry 34
Calculus 67
Engineering
Tables 8
Mechanical
Rigid Bodies
Statics 92
Dynamics 37
Fluid 5
Control
Acoustics 19
Natural Sciences
Matter 1
Electric 27
Biology 1
