Content
Summation of Accumulative Physical Quantity
Probability
Normal Distribution
Probability &
Density Function
Mean
Mean of normal distribution
Mean of a Distribution
Variance
Varance of normal distribution
Varance of a Distribution
Summation of Accumulative Physical Quantity
The application of integration can also be applied to physical quantities other than mechanical quantity such as information about a physical system. In practical applications, when the interested quantity, for example the battery life of auto batteries are continuous random variable, the quantity can be expressed in the form of accumulative quantity. Imply
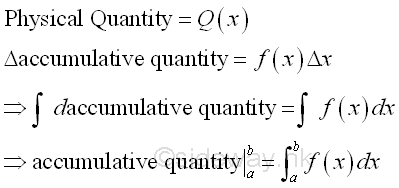
Probability
The information of a system or a product is usually obtained by statistics. The quantifying information through the analysis of sample data can be used to measure performance and to improve quanlity. These quantities are often influenced by variation due to numerous factors which cannot be predicted. And if the values of the quantity are over an interval and the probability distribution of the quantity is known, the variation of quantities can be regarded as the continuous random variable of the function of a probability distribution. In other words, the probability of the quantity over a closed interval [a,b] can be determined from the known probability distribution of the quantity. The quantity distribution is called probability density function and the probability density function is a function of the continuous random variable.
In order to make the probability density function work, the value of the function should always be greater or equal to zero and the summation of all values of the function from the negative infinity to the positive infinity is equal to one, Imply

And the probability P of the quantity of the continuous random variable X over a closed interval [a,b] is
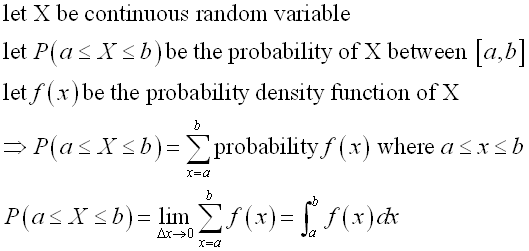
Normal Distribution
The most widely used probability density function is the normal density function f(x) of the normal distribution for a continuous random variable. The normal distribution N(μ,σ2) of a probability density function is in the form of a bell-shaped distribution determined by the Gaussian function.
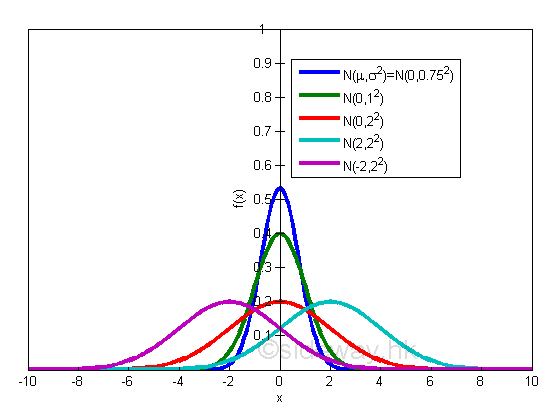
The normal probability density function of a countinuous random variable X with mean μ and variance σ2 is
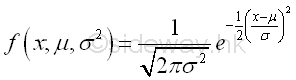
Since the normal probability density function is a probability density function, the value of the function is always greater or equal to zero for all x from the negative infinity to the positive infinity and the summation of all values of the function from the negative infinity to the positive infinity is equal to one. Imply
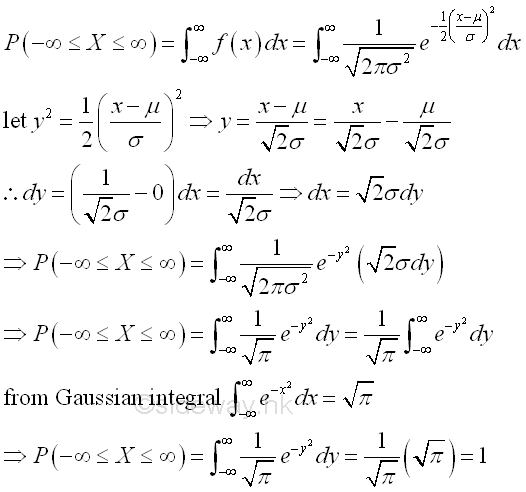
The distribution of the continuous random variable X with specified mean μ and variance σ2 can be obtained by
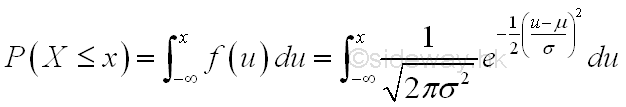
Since the integral of normal probability density function does not have a closed-form solution, numerical methods are required to obtain the solution of a general normal random variable X. For normal random variable X with zero mean and unit variance, the solution may also be obtained via the use of standard normal distribution tables. Therefore a substitution is needed to shift and to scale the variable of integration to the standard form with zero mean and unit variance, that is standard normal distribution N(0,1). The standard continuous random variable Z becomes
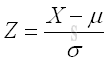
The standard normal density function of the standard continuous random variable Z with mean μ equal to zero and variance σ2 equal to 1 is
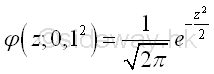
And the standard normal distribution function with the substitution of the continuous random variable Z is
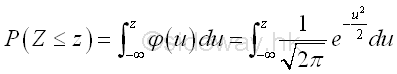
Therefore any normally distributed random variable X can be determined by the standard normal distribution and the value from standard normal distribution tables through the transformation of the variable from x to z according to the given mean and variance . Imply
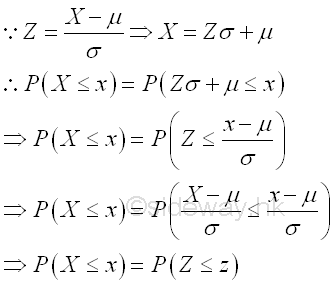
For example, a normally distributed random variable X with mean equal to μ and variance equal to σ2. The probability of random variable X smaller and equal to x is
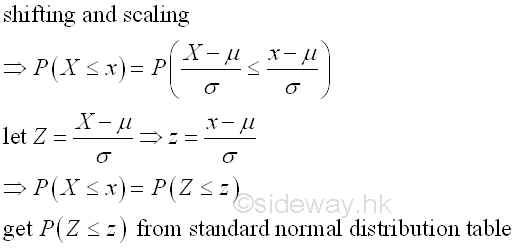
Or, a normally distributed random variable X with mean equal to μ and variance equal to σ2 equal to 1. If the probability of random variable X is pr, then x is

Probability & Density Function
Besides the normal density function, there are many types of simple density function. For example
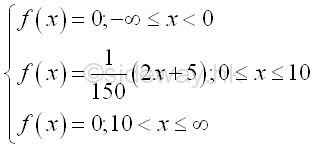
This is a probability density function because the value of the function is greater or equal to zero for all x and the summation of the value of the function for all x is equal to 1, imply
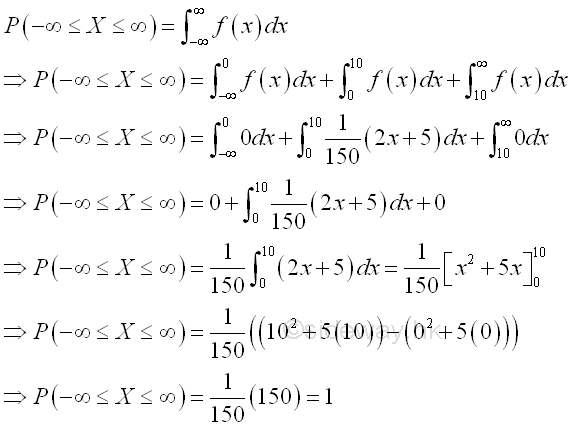
Graphically,
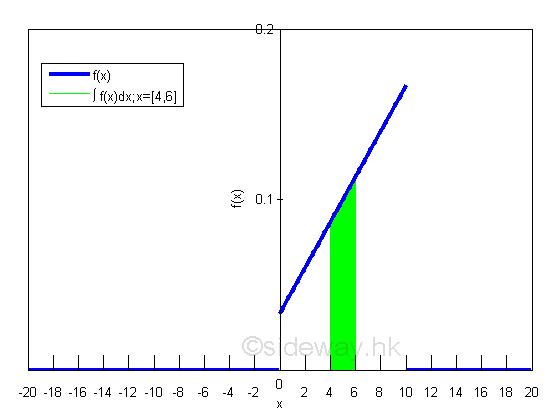
Therefore the probability of X in the closed interval [4,6] can be obtained by integration. For example
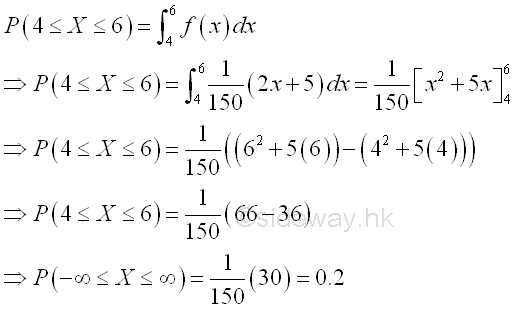
Graphically,

Mean
The value of mean μ is the mean of a distribution with a random variable X. Mean is also known as the mathematical expectation of X. For a continuous random variable X, mean is equal to
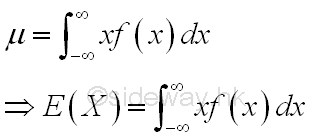
Mean is the weighted average of all items of the continuous random variable X. In the discrete sense, the ratio of percentage of each discrete item is equal to the probability of the discrete item. When the number of discrete items tend to infinite, the probability of variable x can be expressed as a density function of variable x. Imply

Mean of normal distribution
Since the bell shaped normal distribution is symmetrical, the mean of a normal distribution locates at the center of the density function. Imply

Mean of a Distribution
Mean of a distribution with simple density function can also be obtained in similar way. For example
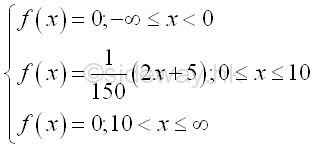
Therefore the mean of the distribution of X is
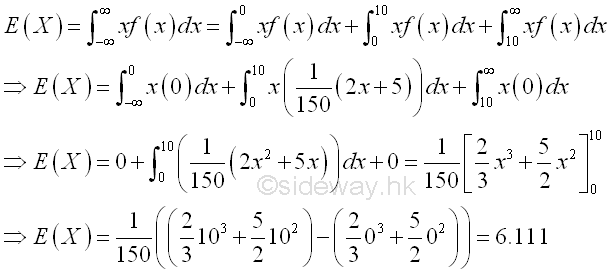
Graphically,
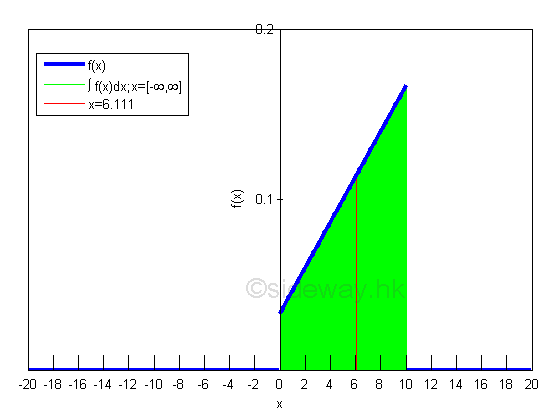
Variance
The value of variance σ2 is used to measure the dispersion of a distribution of the values x of the random variable X. Variance is used to describe the distribution about its degree of the spread of the values x or the degree to which the values x scattered. For a continuous random variable X, variance is equal to
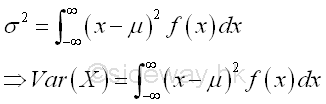
Mean is used as the central reference of the dispersion of a distribution. In order to eliminate the negative value, the difference between the variable and the mean is squared. Variance is therefore the average of the weighted squared difference of all items of a continuous random variable X. In the discrete sense, the ratio of percentage of each discrete item is equal to the probability of the discrete item. When the number of discrete items tend to infinite, the probability of variable x can be expressed as a density function of variable x. Imply

Variance σ2 is therefore the squared deviation of a distribution. And the positive square root of the variance is defined as the standard deviation σ. Imply
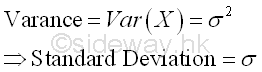
Varance of normal distribution
Since the bell shaped normal distribution is symmetrical and the mean of a normal distribution locates at the center of the density function, the values of a normal distribution is spread symmetrical on each side of the mean. Imply

Varance of a Distribution
Varance of a distribution with simple density function can also be obtained in similar way. For example
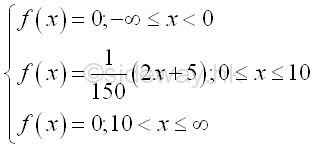
Therefore the varance σ2 of the distribution of X is
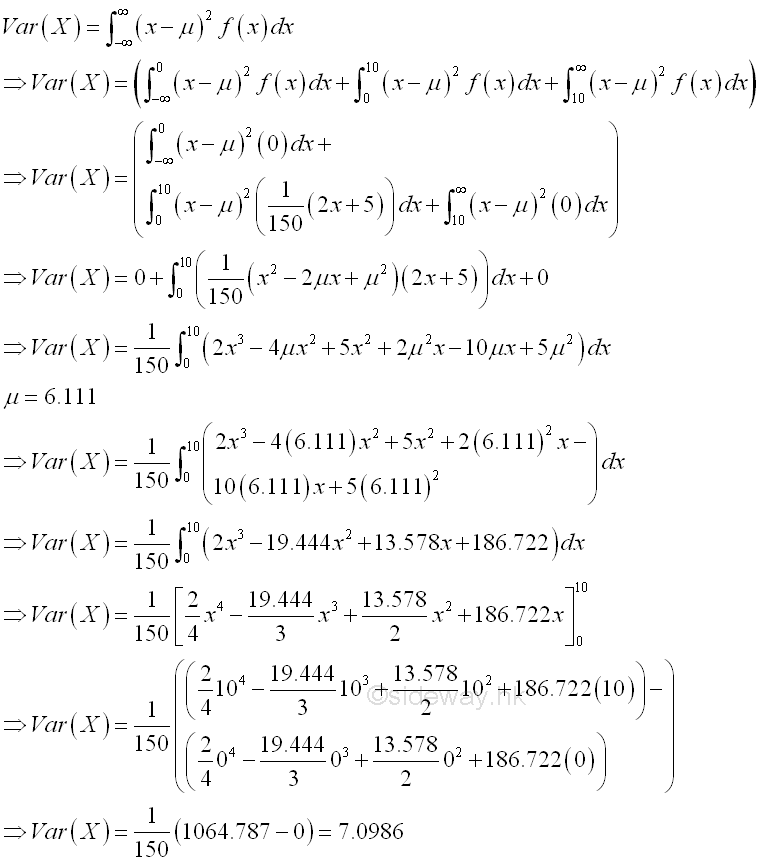
And the standard deviation σ of the distribution of X is
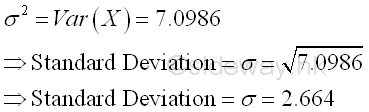
©sideway
ID: 111200013 Last Updated: 1/2/2012 Revision: 0 Ref:
References
- S. James, 1999, Calculus
- B. Joseph, 1978, University Mathematics: A Textbook for Students of Science & Engineering
Latest Updated Links
- Travel Singapore Sight Space(last updated On 12/30/2025)
- Travel Singapore Sight Curiosity Cove(last updated On 12/30/2025)
- Travel Singapore Sight Night Safari(last updated On 12/30/2025)
- Travel Singapore Sight River Wonders(last updated On 12/30/2025)
- Travel Singapore Sight Rainforest Wild ASIA(last updated On 12/30/2025)
- Travel Singapore Sight Singapore Zoo(last updated On 12/30/2025)
- Travel Singapore Sight Mandai(last updated On 12/30/2025)
- Travel Singapore Sight Bird Paradise(last updated On 12/30/2025)
- Travel Singapore Sight AltitudeX(last updated On 12/30/2025)
- Travel Singapore Sight(last updated On 12/6/2025)
- Travel Singapore Rail Network(last updated On 12/5/2025)

 Nu Html Checker
Nu Html Checker  53
53  na
na  na
na
Home 5
Business
Management
HBR 3
Information
Recreation
Hobbies 9
Culture
Chinese 1097
English 339
Travel 31
Reference 79
Hardware 54
Computer
Hardware 259
Software
Application 213
Digitization 37
Latex 52
Manim 205
KB 1
Numeric 19
Programming
Web 289
Unicode 504
HTML 66
CSS 65
SVG 46
ASP.NET 270
OS 431
DeskTop 7
Python 72
Knowledge
Mathematics
Formulas 8
Set 1
Logic 1
Algebra 84
Number Theory 206
Trigonometry 31
Geometry 34
Calculus 67
Engineering
Tables 8
Mechanical
Rigid Bodies
Statics 92
Dynamics 37
Fluid 5
Control
Acoustics 19
Natural Sciences
Matter 1
Electric 27
Biology 1
