Logarithm TheoremPythagorean TheoremCombinatoricsQuadratic EquationsSequence and SeriesLinear AlgebraDiophantine EquationElliptic CurveAlgebra Result
Draft for Information Only
Content
Pythagorean Triples
Example 𝑥3+2𝑦3=3
Source and Reference
Pythagorean Triples
Binary operation on 𝑥2+𝑑𝑦2=1⇒(𝑥,𝑦)⊕(𝑤,𝑧)=(𝑥𝑧−𝑑𝑦𝑤,𝑥𝑤+𝑦𝑧) Consider 𝑥2+𝑑𝑦2=1 over a finite field 𝔽𝑝 Theorem: Wherther or not 𝑑 is a square in 𝔽𝑝, there is a solution 𝑃 such that 𝑍 is generated by 𝑃, i.e. 𝑄=𝑃⊕⋯⊕𝑃 for all 𝑄∊𝑍This single generator is similar to the primitive root mod 𝑃
Proof: Consider the field ext 𝐾=𝔽𝑝(√𝑑). Denote: [𝑛]𝑃=𝑃⊕⋯⊕𝑃. Define 𝑓:𝑍→𝐾 by 𝑓(𝑄)=𝑥+𝑦√𝑑 with rational solution (𝑥,𝑦).
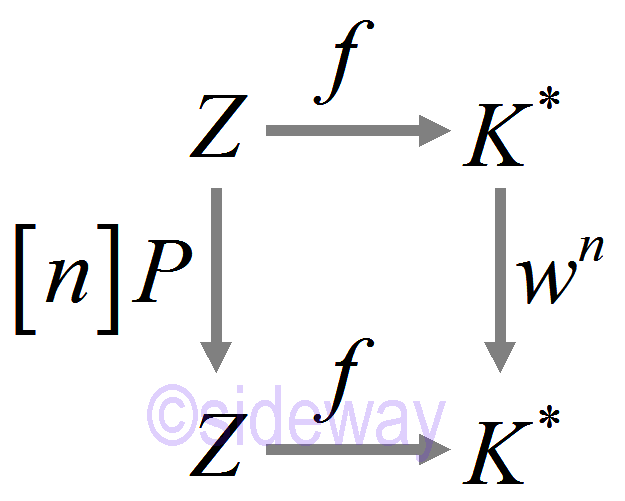 Existence of a primitive root: 𝑔∊𝐾 s.t. {𝑔𝑛: 𝑛=0, 1, ⋯}=𝐾*. □
Fact: A subset of finitely many solutions will not generate 𝑍 under the operation.
Key ingredients for parameterisation: 𝑥2+𝑑𝑦2=1
Existence of a primitive root: 𝑔∊𝐾 s.t. {𝑔𝑛: 𝑛=0, 1, ⋯}=𝐾*. □
Fact: A subset of finitely many solutions will not generate 𝑍 under the operation.
Key ingredients for parameterisation: 𝑥2+𝑑𝑦2=1- A rational point (1,0)
- The degree being 2⇒𝑚−1: 𝑄→𝑍0
Idea: One rational point and a tangent line → given a rational point.
Intesection to degree 2 such that a cubic curve of degree 3 to degree 2 and the tangent line with
Example 𝑥3+2𝑦3=3
𝑍={𝑥3+2𝑦3=3}. 𝑃=(1,1)∊𝑍. Let 𝐹(𝑥,𝑦)=𝑥3+2𝑦3−3 tangent line at (𝑎,𝑏)=∂𝐹∂𝑥(𝑥−𝑎)+
∂𝐹∂𝑦(𝑦−𝑏)=3𝑎2(𝑥−𝑎)+6𝑏2(𝑦−𝑏)=0 So 3(𝑥−1)+6(𝑦−1)=0 and 𝑥3+2𝑦3=3 subst. 𝑧=𝑥−1, 𝑤=𝑦−1 3𝑧+6𝑤=0 and (𝑧+1)3+2(𝑤+1)3=3 6𝑤2(3−𝑤)=0⇒𝑤=3⇒𝑦=4, 𝑥=−5 Idea: repeat with (−5,4) Line: 25(𝑥+5)+32(𝑦−4)=0 and 𝑥3+2𝑦3=3 subst. 𝑧=𝑥+5, 𝑤=𝑦−4 𝑥=655/253, 𝑦=−488/253, 253=11*23 Therefore (1,1)→(−5,4)→(655/253,−488/253)
Idea: Two rational points and a secant line→a rational point
−
741253(𝑥−1)−
402253(𝑦−1)=0 and 𝑥3+2𝑦3=3 subst. 𝑧=𝑥−1, 𝑤=𝑦−1 741𝑧+402𝑤=0 and (𝑧+1)3+2(𝑤+1)3=3
27732342𝑤315069223+
419922𝑤261009+
1080𝑤247=0 Therefore 𝑤→0, −
741253(𝑥−1)=0⇒𝑤
741253
741253
27732342𝑤15069223+
9108061009
2630918269, 𝑦=
344918269⇒𝑥≈1.44, 𝑦≈0.18 Tangent line, 𝑃⊕𝑄 and Secant line, 𝑃 ⇒𝑅 Mordell-Weil Theorem: There are a finite subset of solutions that generate all solutions.
Source and Reference
https://www.youtube.com/watch?v=hrp0GdsqLEghttps://www.youtube.com/watch?v=PZlVYEihCh0
©sideway
ID: 201100017 Last Updated: 11/17/2020 Revision: 0 Ref:
References
- B. Joseph, 1978, University Mathematics: A Textbook for Students of Science & Engineering
- Wheatstone, C., 1854, On the Formation of Powers from Arithmetical Progressions
- Stroud, K.A., 2001, Engineering Mathematics
- Coolidge, J.L., 1949, The Story of The Binomial Theorem
Latest Updated Links
- Travel Singapore Sight Central(last updated On 1/8/2026)
- Panasonic HHGTQ1001B13 LED Floor Light(last updated On 1/7/2026)
- Travel Singapore Sight West | Central(last updated On 1/6/2026)
- Travel Singapore Sight Sentosa Sensoryscape(last updated On 1/5/2026)
- Travel Singapore Sight Sentosa Resorts World Sentosa(last updated On 1/4/2026)
- Travel Singapore Sight Sentosa HarbourFront(last updated On 1/3/2026)
- Travel Singapore Sight Sentosa(last updated On 1/2/2026)
- Travel Singapore Sight Bird Paradise(last updated On 12/30/2025)
- Travel Singapore Sight Mandai(last updated On 12/30/2025)
- Travel Singapore Sight Singapore Zoo(last updated On 12/30/2025)
- Travel Singapore Sight Rainforest Wild ASIA(last updated On 12/30/2025)

 Nu Html Checker
Nu Html Checker  53
53  na
na  na
na
Home 5
Business
Management
HBR 3
Information
Recreation
Hobbies 9
Culture
Chinese 1097
English 339
Travel 38
Reference 79
Hardware 55
Computer
Hardware 259
Software
Application 213
Digitization 37
Latex 52
Manim 205
KB 1
Numeric 19
Programming
Web 289
Unicode 504
HTML 66
CSS 65
SVG 46
ASP.NET 270
OS 431
DeskTop 7
Python 72
Knowledge
Mathematics
Formulas 8
Set 1
Logic 1
Algebra 84
Number Theory 206
Trigonometry 31
Geometry 34
Calculus 67
Engineering
Tables 8
Mechanical
Rigid Bodies
Statics 92
Dynamics 37
Fluid 5
Control
Acoustics 19
Natural Sciences
Matter 1
Electric 27
Biology 1
