Content
Equilibrium in Two Dimensions
Reactions at Supports and Connections
Equilibrium in Two Dimensions
Many practical engineering problem can be considered as a planar rigid body in two dimensions. The conditions for the equilibrium of a rigid body is.
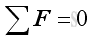 and
and
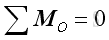
By neglecting the z axis dimension. Imply
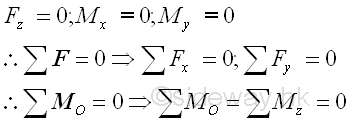
When a rigid body is in static equilibrium state, the moment at any point A in the planar structure is equal to zero also, imply
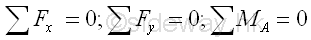
Only two translational and one rotational motion are needed for determining a two dimensional structure is in static equilibrium state or not.
In other words, the possible forces and moments due to an applied action or a reaction in a two dimensional structure are two rectangular forces and one moment, or one resultant force and one moment.
Since there are only three equations obtained from the equilibrium equations of a rigid body in two dimenstion, no more than three unknowns can be determined by the system of three equations.
Reactions at Supports and Connections
In order to construct the free body diagram for analysing the equilibrium of rigid body in two dimensions, the types of reactions at supports and connections should be evaluated first. The types of reactions at supports and connections can be divided into three types:
-
Reactions equivalent to a force and a couple
For fixed support, no translational motion and rotation motion is allowed for the free body to move and thus the free body is fully constrained.

The resultant reactions are equal to one resultant force and one couple, or two rectangular force components of the resultant force and one moment of the couple.
-
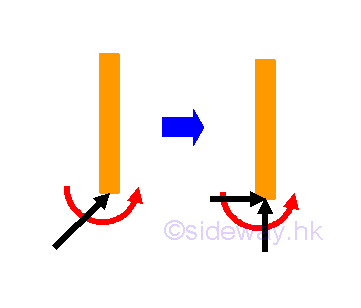
Reactions equivalent to a force
For hinged support or connection, the rotational motion is enabled by equipping with a fictionless hinge or pin, or a free or rounded end, no couple is reacted by the support or connection on the free body. But, the translational motion is stopped by either the reaction force of the hinge support or the friction force generated by the rough surface.
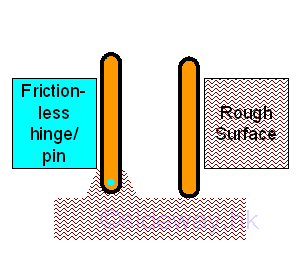
The resultant reactions is equal to one resultant force, or two rectangular force components of the resultant force.
-
Reactions equivalent to a force with known line of actionown line of action
-
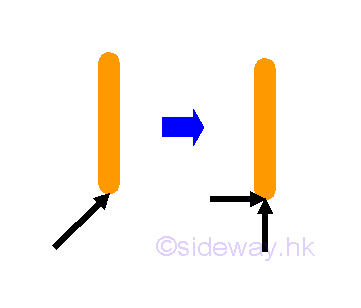
For roller support or connection
The rotational motion is enabled by equipping with a fictionless hinge or pin, or a free or round end, no couple is reacted by the support or connection on the free body. Besides the roller motion also allows a free translational motion in the direction along the frictionless surface. The roller motion can be a roller wheel, a guided roller, a rocker on a smooth surface, or a free or rounded end on a smooth surface. Although one component of the rectangular reaction force is equal to zero, the translational motion is still constrained by the other component of the rectangular force generated by the support or connection
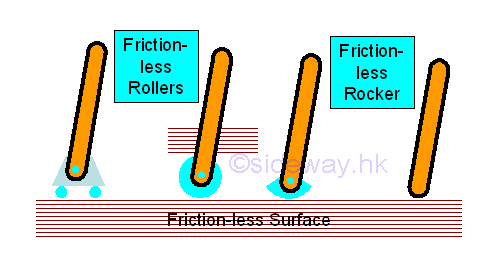
The resultant reaction are equal to one reaction force which is always normal to the non-constrained free motion direction.
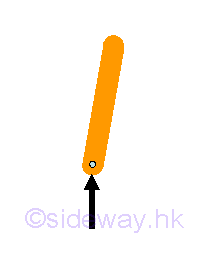
-
For free sliding guide with hinge pin support or connection
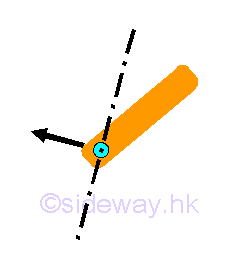
The rotational motion is enabled by equipping with a fictionless hinge or pin, no couple is reacted by the support or connection on the free body. Besides the free sliding guide also allows a free translational motion in the sliding direction. The free sliding guide can be a frictionless pin in slot, or a collar on a frictionless rod. Although one component of the rectangular reaction force is equal to zero, the translational motion is still constrained by the other component of the rectangular force generated by the support or connection
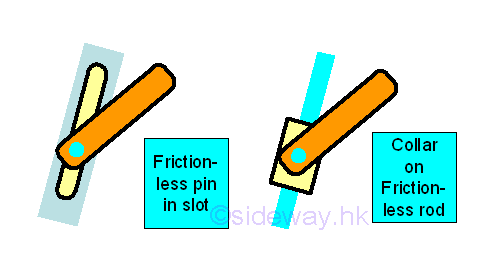
The resultant reaction are equal to one reaction force which is always normal to the non-constrained free motion direction.
-
For free short cable or link support or connection
For a cable, the only possible reaction force is the tension of the cable. For a free short link, the rotational motion is enabled by equipping with two fictionless hinge or pin on both ends of the link, no couple is reacted by the support or connection on the free body. Because of the two frictionless hinge on both sides of the link, any translational motion normal to the link becomes a free rotation motion of the link about the other end of the link. Therefore a free short link also allows a free translational motion normal to the connecting axis of the link. Although one component of the rectangular reaction force is equal to zero, the translational motion is still constrained by the other component of the rectangular force generated by the support or connection. Therefore both a free short cable and link provide only one constraint along the cable or link to the free body.
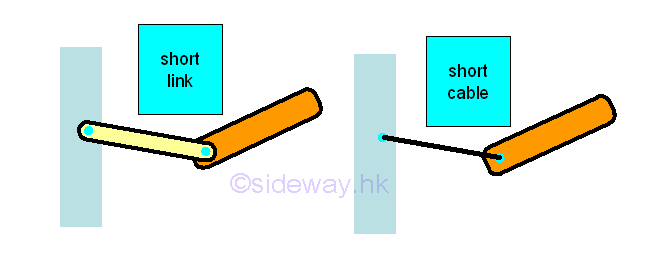
The resultant reaction are equal to one reaction force which is always align with the connecting axis of the cable or link. And for the cable, the reaction force is always away from the free body.
-
©sideway
ID: 120200061 Last Updated: 2/16/2012 Revision: 0 Ref:
References
- I.C. Jong; B.G. rogers, 1991, Engineering Mechanics: Statics and Dynamics
- F.P. Beer; E.R. Johnston,Jr.; E.R. Eisenberg, 2004, Vector Mechanics for Engineers: Statics
Latest Updated Links
- Travel Singapore Sight Singapore Zoo(last updated On 12/30/2025)
- Travel Singapore Sight Mandai(last updated On 12/30/2025)
- Travel Singapore Sight Bird Paradise(last updated On 12/30/2025)
- Travel Singapore Sight Rainforest Wild ASIA(last updated On 12/10/2025)
- Travel Singapore Sight(last updated On 12/6/2025)
- Travel Singapore Rail Network(last updated On 12/5/2025)
- Travel Singapore Things to Know(last updated On 12/4/2025)
- Travel Singapore(last updated On 12/3/2025)
- Legrand Galion(last updated On 12/2/2025)
- Schneider Electric AvatarOn(last updated On 12/1/2025)
- Alfalux(last updated On 11/30/2025)

 Nu Html Checker
Nu Html Checker  53
53  na
na  na
na
Home 5
Business
Management
HBR 3
Information
Recreation
Hobbies 9
Culture
Chinese 1097
English 339
Travel 26
Reference 79
Hardware 54
Computer
Hardware 259
Software
Application 213
Digitization 37
Latex 52
Manim 205
KB 1
Numeric 19
Programming
Web 289
Unicode 504
HTML 66
CSS 65
SVG 46
ASP.NET 270
OS 431
DeskTop 7
Python 72
Knowledge
Mathematics
Formulas 8
Set 1
Logic 1
Algebra 84
Number Theory 206
Trigonometry 31
Geometry 34
Calculus 67
Engineering
Tables 8
Mechanical
Rigid Bodies
Statics 92
Dynamics 37
Fluid 5
Control
Acoustics 19
Natural Sciences
Matter 1
Electric 27
Biology 1
