Content
Centroid of 2D
Plane Body
Centroids of
Lines
Curve
Length of Quarter-Circular Arc by Integration
Centroid of
Quarter-Circular Arc
by Integration
Centroid of
Semi-Circular Arc
by Integration
Centroid of
Circular Arc
by Integration
Centroid of 2D Plane Body
The centroid of an plate is determined by the first moment of a two dimensional plane body with the method of the first moment of area.
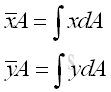
And the centroid of a wire is determined by the first moment of a two dimensional plane body with the method of the first moment of line.
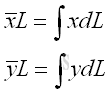
Centroids of Lines
Curve Length of Quarter-Circular Arc by Integration
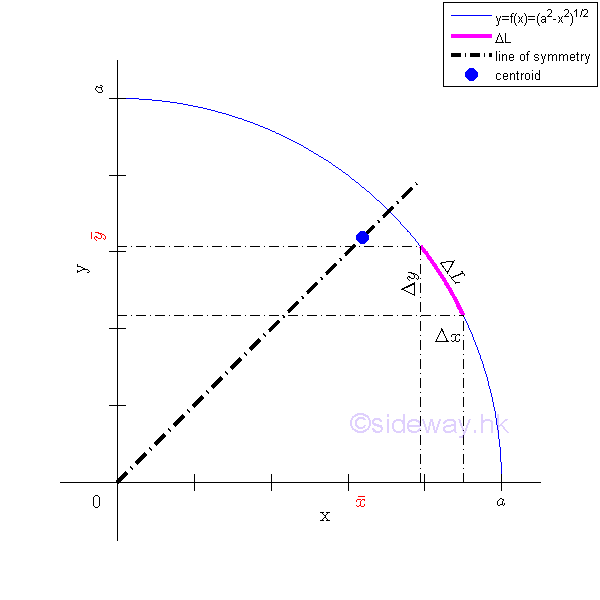
For example, the curve segment bounded by curves in rectangular form , Imply
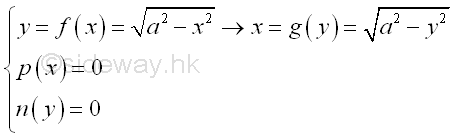
An elemental curve fragment ΔL in rectangular form can be approximated by pythagorean theorem. Imply
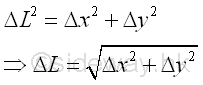
By taking the limit, the dimension of the curve element can be expressed as
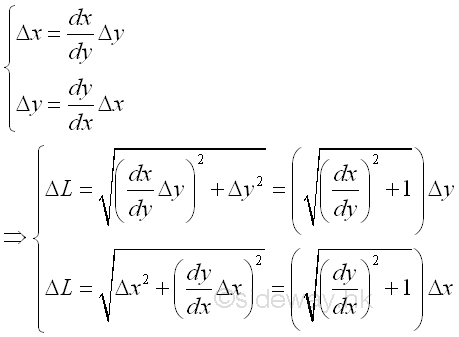
In general, the length of the curce in a region can be determined by integration through sweeping the curve element along either rectangular coordinate axis. Imply
Sweeping along x axis horizontally

The length of the curce in a region can also be determined by integration through sweeping the curve element along y axis in similar way.
Centroid of Quarter-Circular Arc by Integration
The centroid of the planar curve can be determined by a single integration through sweeping the elemental centroid of the curve fragment along either rectangular coordinate axis.
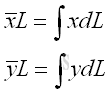
Sweeping along y axis vertically
The x coordinate of centroid of the planar curve is.
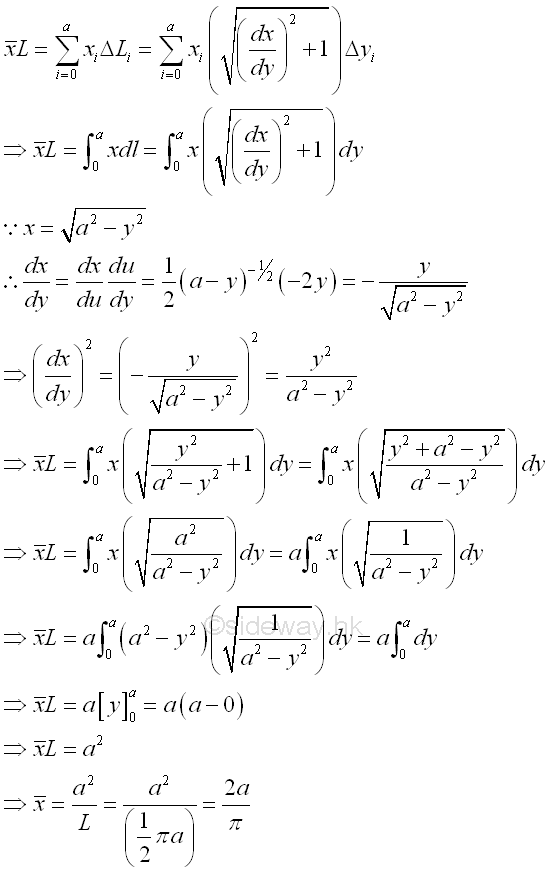
The y coordinate of centroid of the planar curve is.
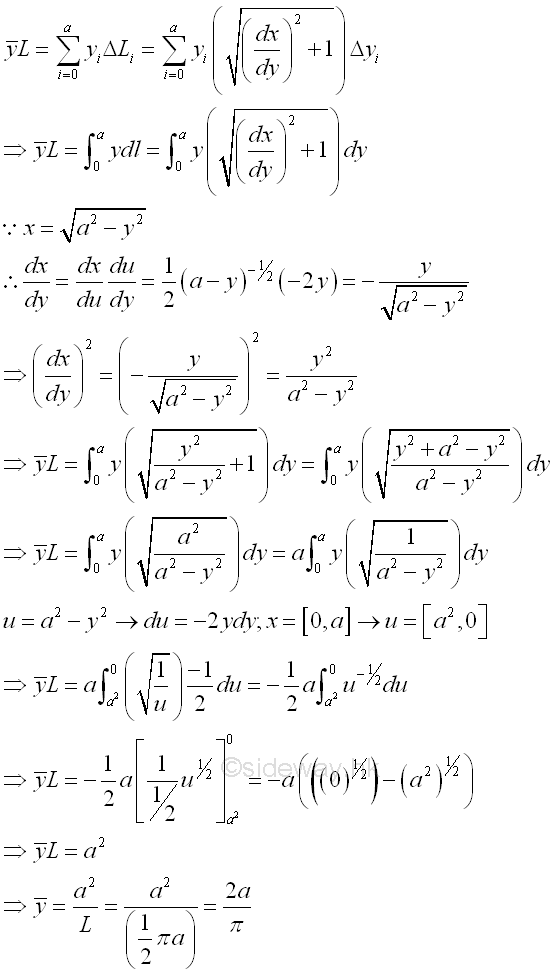
Centroid of Semi-Circular Arc by Integration
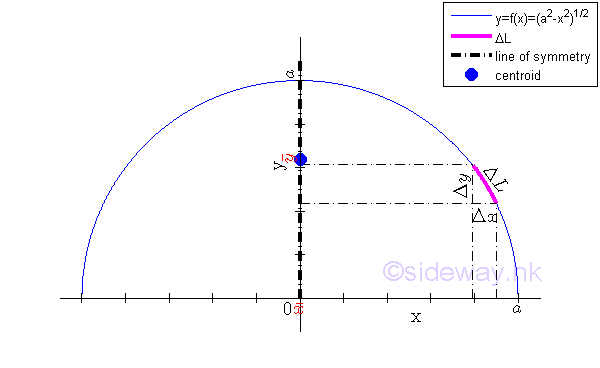
For example, the curve segment bounded by curve in rectangular form , Imply
By symmetry, the length of a semi-circular arc is
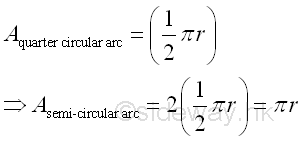
The centroid of the planar curve can be determined by a single integration through sweeping the elemental centroid of the curve fragment along either rectangular coordinate axis.
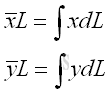
Sweeping along x axis horizonatally
Coordinate x of centroid by symmetry.
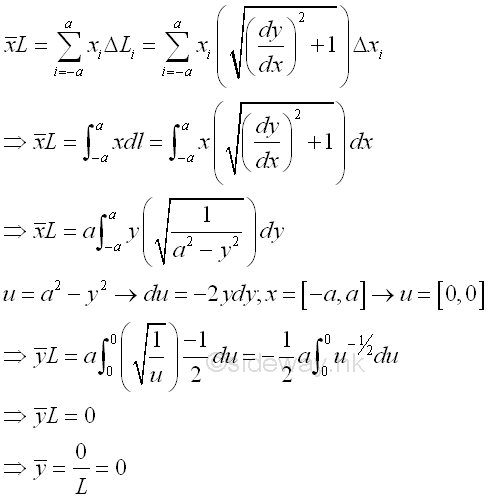
Coordinate x of centroid by integration.
Centroid of Circular Arc by Integration
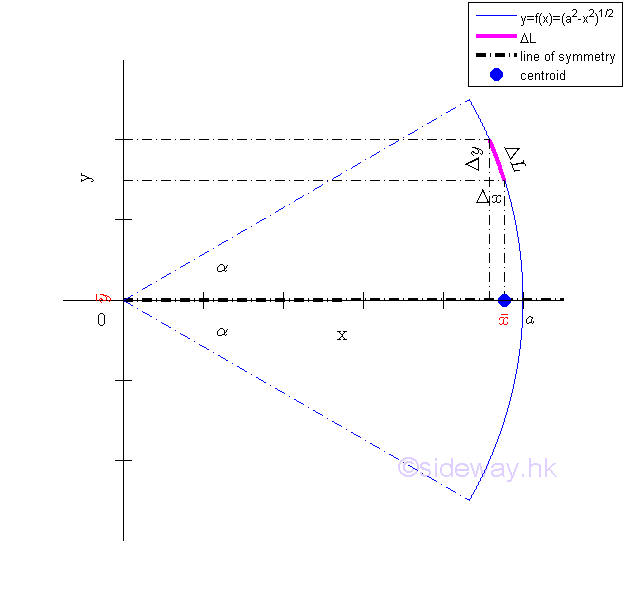
For example, the curve segment bounded by curve in polar form , Imply
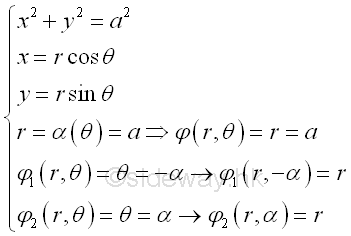
The length of the curve segment
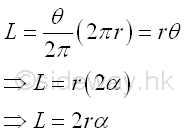
The centroid of the planar curve can be determined by a single integration through sweeping the elemental centroid of the curve fragment along variable angle c circularly.
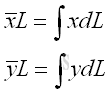
By sweeping the centroid of circular sector slice along variable angle θ circularly
Coordinate x of centroid by integration. Imply
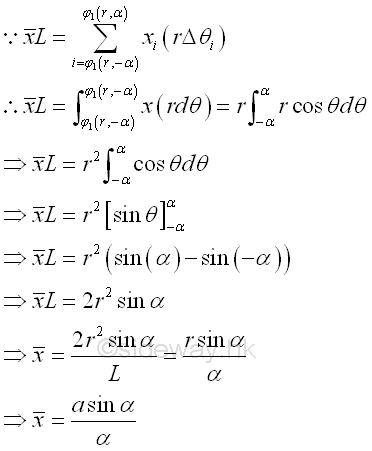
Coordinate y of centroid by symmetry. Imply
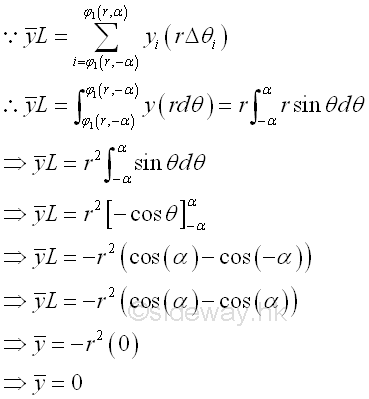
©sideway
ID: 120600006 Last Updated: 6/7/2012 Revision: 0 Ref:
References
- I.C. Jong; B.G. rogers, 1991, Engineering Mechanics: Statics and Dynamics
- F.P. Beer; E.R. Johnston,Jr.; E.R. Eisenberg, 2004, Vector Mechanics for Engineers: Statics
Latest Updated Links
- Travel Singapore Sight West | Central(last updated On 1/6/2026)
- Travel Singapore Sight Sentosa Sensoryscape(last updated On 1/5/2026)
- Travel Singapore Sight Sentosa Resorts World Sentosa(last updated On 1/4/2026)
- Travel Singapore Sight Sentosa HarbourFront(last updated On 1/3/2026)
- Travel Singapore Sight Sentosa(last updated On 1/2/2026)
- Travel Singapore Sight River Wonders(last updated On 12/30/2025)
- Travel Singapore Sight Bird Paradise(last updated On 12/30/2025)
- Travel Singapore Sight Mandai(last updated On 12/30/2025)
- Travel Singapore Sight Rainforest Wild ASIA(last updated On 12/30/2025)
- Travel Singapore Sight Night Safari(last updated On 12/30/2025)
- Travel Singapore Sight Curiosity Cove(last updated On 12/30/2025)

 Nu Html Checker
Nu Html Checker  53
53  na
na  na
na
Home 5
Business
Management
HBR 3
Information
Recreation
Hobbies 9
Culture
Chinese 1097
English 339
Travel 37
Reference 79
Hardware 54
Computer
Hardware 259
Software
Application 213
Digitization 37
Latex 52
Manim 205
KB 1
Numeric 19
Programming
Web 289
Unicode 504
HTML 66
CSS 65
SVG 46
ASP.NET 270
OS 431
DeskTop 7
Python 72
Knowledge
Mathematics
Formulas 8
Set 1
Logic 1
Algebra 84
Number Theory 206
Trigonometry 31
Geometry 34
Calculus 67
Engineering
Tables 8
Mechanical
Rigid Bodies
Statics 92
Dynamics 37
Fluid 5
Control
Acoustics 19
Natural Sciences
Matter 1
Electric 27
Biology 1
