Content
Examples of
Friction Forces
Sliding Block on inclined board
Ladder
on Wall Problem
Ladder
on Edge Problem
Examples of Friction Forces
Frictional forces can be found in common practical engineering problems.
Sliding Block on inclined board
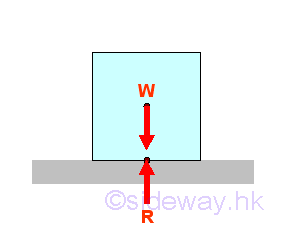
When a sliding block is placed on a horizontal board without subject to other force, there are only the weight W and the reaction R. The reaction force R balances the weight W. Since there is no horizontal force component acts on the contact surfaces, the friction force between the surfaces of contact is zero also.
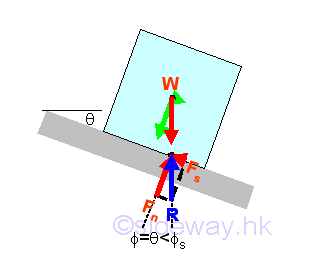
When increasing the inclination of the board by a small angle θ, the reaction force R which balances the weight W, will deviate from the normal of the board surface by the angle θ also. The reaction force R can be converted into normal component Fn of magnitude W cos θ and tangential component Fs of magnitude W sin θ with respect to the board surface through force discomposition. If the magnitude of the tangential component of the weight W is less than the maximum static friction force Fs,max , the reactive friction force Fs is equal to the W sin θ also. And the angle of inclination θ of the board is equal to the angle of friction but the angle of friction is smaller than the angle of static friction.
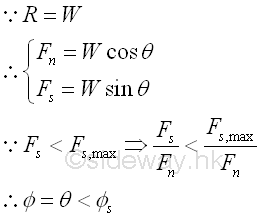
When the motion of solid body is impending.
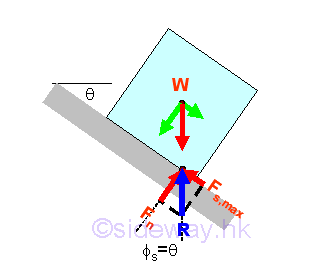
When increasing the angle of inclination θ, the tangential component of the weight along the board surface will increase also. This tangential force which causes the sliding down motion of the block, should be balanced by the static friction force. When the angle of inclination θ is increased to cause the solid body to just about to move, the angle of inclination is called the angle of repose. Since the block is in static equilibrium, the reaction R is equal to the weight W. Similarly, the reaction force R can be converted into normal component Fn of magnitude W cos θ and tangential component Fs,max of magnitude W sin θ with respect to the board surface through force discomposition. If the magnitude of the tangential component of the weight W is balanced by the maximum static friction force Fs,max , the reactive friction force Fs,max is equal to the W sin θ also. And the angle of inclination θ of the board is equal to the angle of static friction øs also. imply
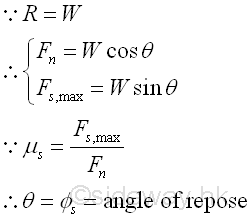
When the solid body is sliding.
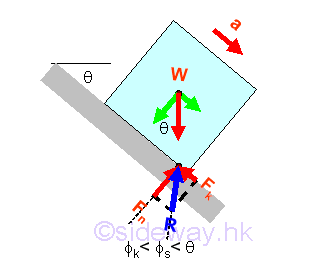
The further increasing of the angle of inclination θ, the tangential component of the weight along the board surface will further increase also. Since the further increased tangential force due to the weight cannot be balanced by the maximum static friction force any more, the incresed tangential force will cause the block to move and to slide down. Because the maximum static friction force is smaller than the tangential component of the weight, the resultant reaction force R is smaller than the weight W. Similarly, when the block is sliding, the reaction force R can be converted into normal component Fn of magnitude W cos θ and tangential component Fk of magnitude μkFn with respect to the board surface through force discomposition. Since the normal component of reaction Fn is equal to the normal component of weight W, and the tangential component of reaction Fk is smaller than the tangential component of weight W, the angle of kinetic friction øs is smaller than the angle of inclination θ also. Imply
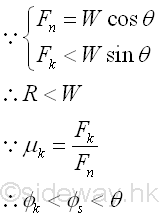
Therefore by increasing the angle of inclination, the maximum possible position of the point of application of the weight W on the contact surfaces is at the corner of block. Imply
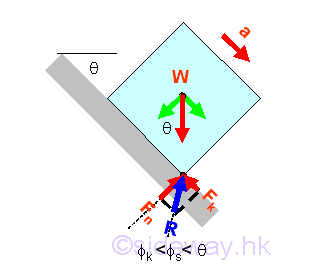
If the magnitude of the tangential component of the weight W is less than the maximum value of the static friction force Fs,max when the point of application shifting to the corner of the block, the further increasing the magnitude of the anlge of inclination will tip over the block about the corner of the block because of the formed resultant couple WF.
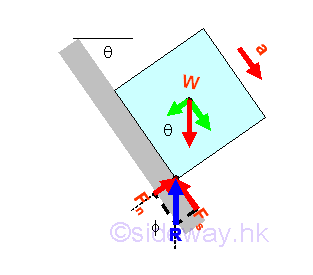
Ladder on Wall Problem
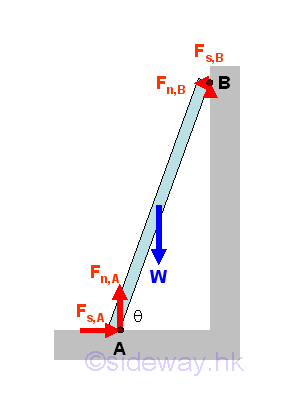
A ladder leans against a wall at angle θ with friction of identical friction coefficients μ acts at both A and B. The minimum value of friction coefficient for the ladder such that the ladder will stand without slipping can be determined by equilibrium equations. Imply
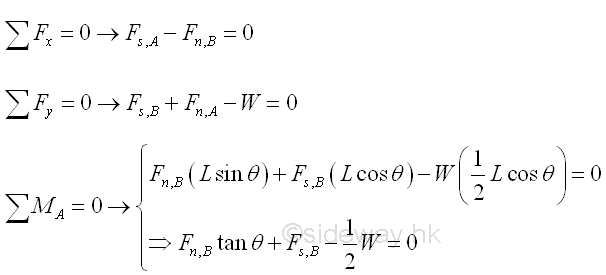
Besides, for friction of identical friction coefficeints, imply
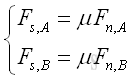
The minimum value of friction coefficient is
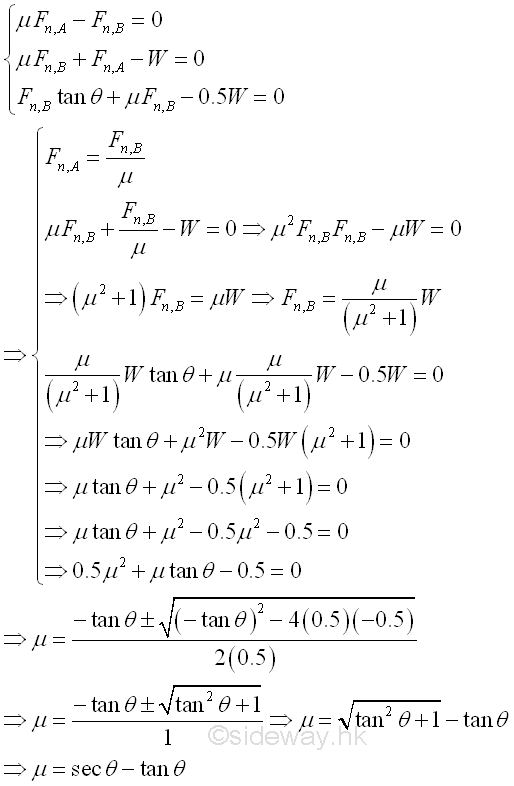
Therefore, the reaction forces of the ladder are
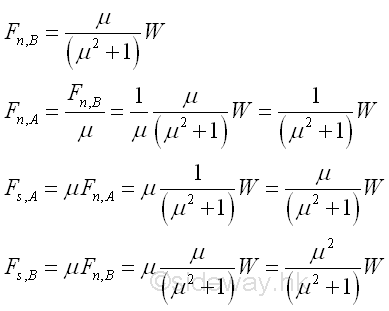
Ladder on Edge Problem
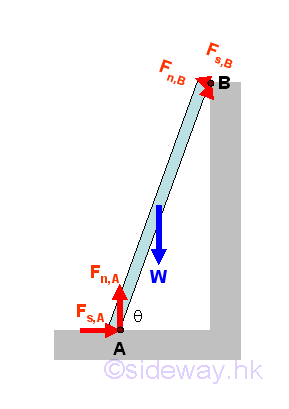
A ladder leans against an edge at angle θ with friction of identical friction coefficients μ acts at both A and B. The minimum value of friction coefficient for the ladder such that the ladder will stand without slipping can be determined by equilibrium equations. Imply
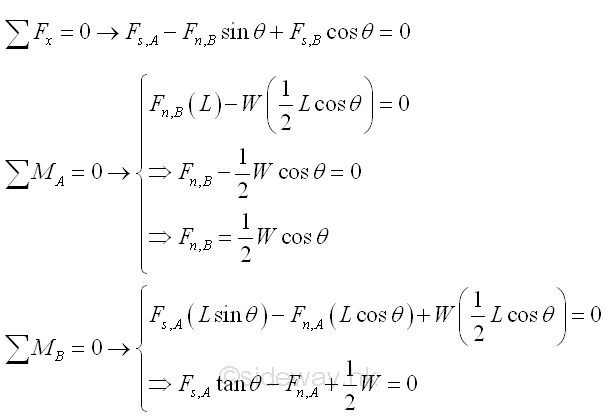
Besides, for friction of identical friction coefficeints, imply
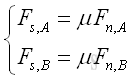
The minimum value of friction coefficient is
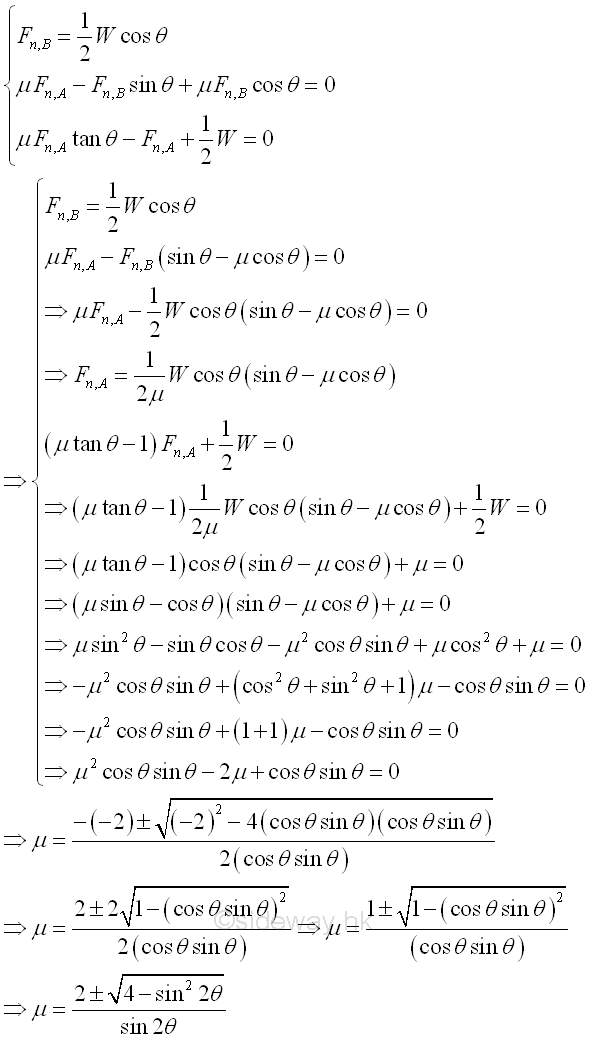
Therefore, the reaction forces of the ladder are
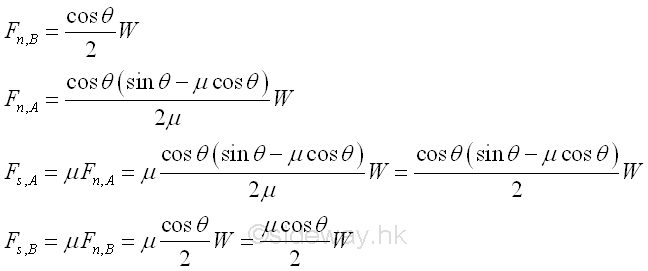
©sideway
ID: 120800001 Last Updated: 8/2/2012 Revision: 0 Ref:
References
- I.C. Jong; B.G. rogers, 1991, Engineering Mechanics: Statics and Dynamics
- F.P. Beer; E.R. Johnston,Jr.; E.R. Eisenberg, 2004, Vector Mechanics for Engineers: Statics
Latest Updated Links
- Travel Singapore Sight Sentosa Sensoryscape(last updated On 1/5/2026)
- Travel Singapore Sight Sentosa Resorts World Sentosa(last updated On 1/4/2026)
- Travel Singapore Sight Sentosa HarbourFront(last updated On 1/3/2026)
- Travel Singapore Sight Sentosa(last updated On 1/2/2026)
- Travel Singapore Sight Singapore Zoo(last updated On 12/30/2025)
- Travel Singapore Sight Mandai(last updated On 12/30/2025)
- Travel Singapore Sight Rainforest Wild ASIA(last updated On 12/30/2025)
- Travel Singapore Sight River Wonders(last updated On 12/30/2025)
- Travel Singapore Sight Night Safari(last updated On 12/30/2025)
- Travel Singapore Sight Curiosity Cove(last updated On 12/30/2025)
- Travel Singapore Sight Space(last updated On 12/30/2025)

 Nu Html Checker
Nu Html Checker  53
53  na
na  na
na
Home 5
Business
Management
HBR 3
Information
Recreation
Hobbies 9
Culture
Chinese 1097
English 339
Travel 35
Reference 79
Hardware 54
Computer
Hardware 259
Software
Application 213
Digitization 37
Latex 52
Manim 205
KB 1
Numeric 19
Programming
Web 289
Unicode 504
HTML 66
CSS 65
SVG 46
ASP.NET 270
OS 431
DeskTop 7
Python 72
Knowledge
Mathematics
Formulas 8
Set 1
Logic 1
Algebra 84
Number Theory 206
Trigonometry 31
Geometry 34
Calculus 67
Engineering
Tables 8
Mechanical
Rigid Bodies
Statics 92
Dynamics 37
Fluid 5
Control
Acoustics 19
Natural Sciences
Matter 1
Electric 27
Biology 1
