Moment of a force in 2D about a point
When an application is subjected to coplanar forces, forces in a plane and the effect of the depth on structure analysis is negligible, the problem can be simplified into two dimensional analysis. Because the direction of moment of a force is always normal to the plane joining the reference point and the line of action, the moment of forces in a plane about a point can therefore refer to the sense of the moment about a point.
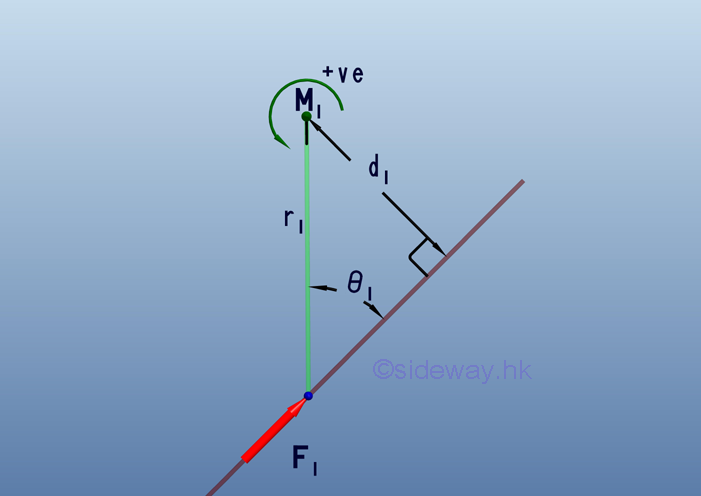
According to the right hand rule, a counterclockwise moment about a reference point can be taken as positive, while a clockwise moment about a reference point can be taken as negative.

Moment Addition of Coplanar Forces
The total moment of forces about a reference point can be determined by adding up all moments of forces.
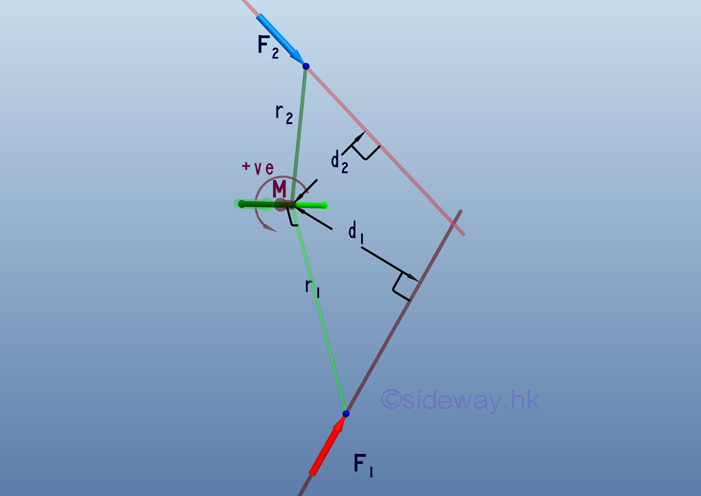
Therefore, the magnitude of the effective moment , M, can be expressed as:
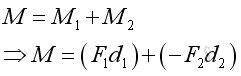
Moment of Concurrent Forces
For concurrent forces, the moment of the resultant of concurrent forces is also equal to the resultant force times the prependicular distance between the reference point and the line of action of the rusultant force. The effective moment can also be computed by adding up all individual moment of concurrent forces.
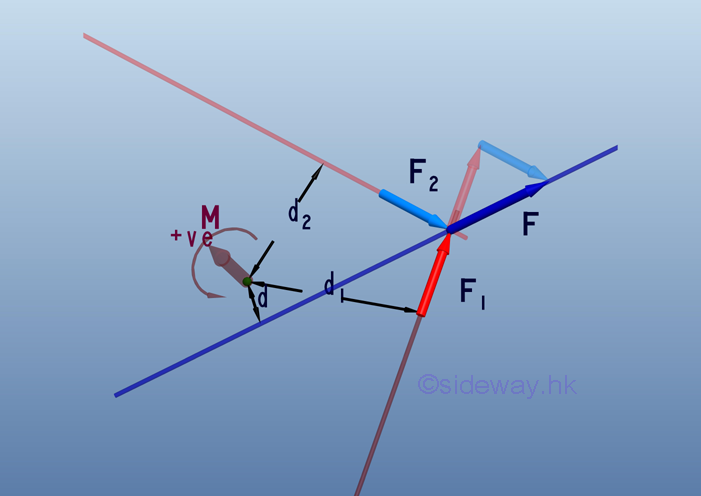
Therefore, the magnitude of the moment , M, can be expressed as:
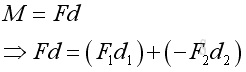
Moment Decomposition
Since the effective moment of concurrent forces about a reference point is equal to the sum of the moments of the concurrent forces as stated in Varignon's Theorem. In other words, moment of a force can also be decomposed through force decomposition.
A force, F in a plane can be decomposed into two retangular components, Fx and Fy. The moment, M of force, F can therefore be decomposed into MFx and MFy.
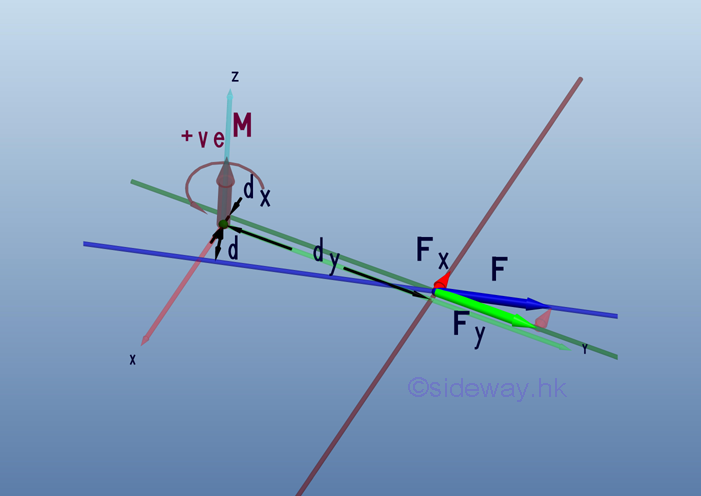
Therefore, the magnitude of the moment , M, can be expressed as:
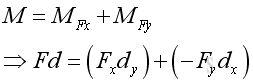
Moment Vector
When the force vector is decomposed into two rectangular components, the corresponding perpendicular distance components are also equal to the magnitudes of the two rectangular components of the postition vector, r of the point of application. And the moment vector, M becomes the third dimension of the rectangular coordinate system.
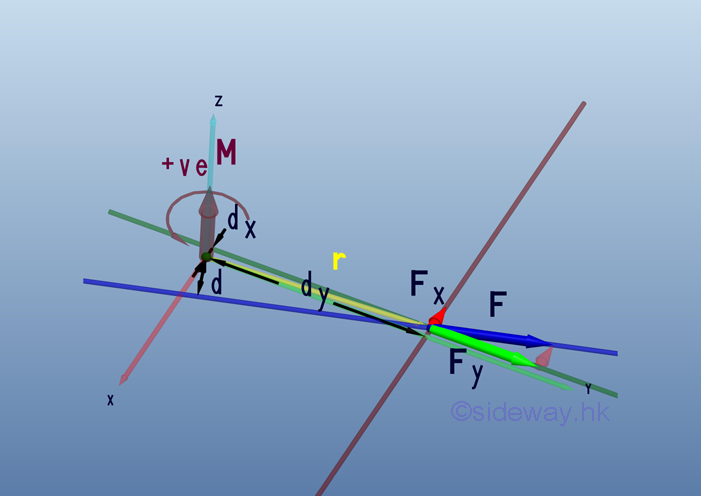
Therefore the force vector, F and position vector, r can be expressed as:
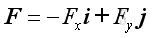 and
and
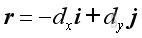
where the minus sign indicates the direction as usual
The moment of a force, M about a reference point can be defined as the vector product of r and F.
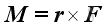
Imply
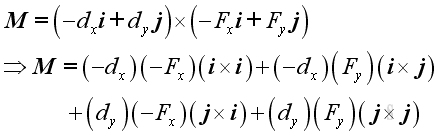
Since the magnitude of vector product is the product of the magnitudes of the two vectors and the sine of the angle formed by the vectors, imply
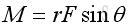
Therefore, the vector product of a unit vector with itselt is equal to a zero vector, imply
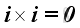 and
and
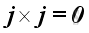
For the sense of the direction, the vector product of two different unit vectors is equal to the unit vector in the third dimension according to the right hand rule, imply
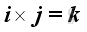 and
and
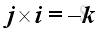
Substitute all variables into the moment vector equation, imply
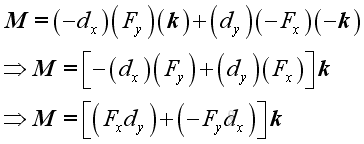
©sideway
ID: 110600001 Last Updated: 6/9/2011 Revision: 1 Ref:
References
- I.C. Jong; B.G. rogers, 1991, Engineering Mechanics: Statics and Dynamics
- F.P. Beer; E.R. Johnston,Jr.; E.R. Eisenberg, 2004, Vector Mechanics for Engineers: Statics
Latest Updated Links
- Travel Singapore Sight Space(last updated On 12/30/2025)
- Travel Singapore Sight Curiosity Cove(last updated On 12/30/2025)
- Travel Singapore Sight Night Safari(last updated On 12/30/2025)
- Travel Singapore Sight River Wonders(last updated On 12/30/2025)
- Travel Singapore Sight Rainforest Wild ASIA(last updated On 12/30/2025)
- Travel Singapore Sight Singapore Zoo(last updated On 12/30/2025)
- Travel Singapore Sight Mandai(last updated On 12/30/2025)
- Travel Singapore Sight Bird Paradise(last updated On 12/30/2025)
- Travel Singapore Sight AltitudeX(last updated On 12/30/2025)
- Travel Singapore Sight(last updated On 12/6/2025)
- Travel Singapore Rail Network(last updated On 12/5/2025)

 Nu Html Checker
Nu Html Checker  53
53  na
na  na
na
Home 5
Business
Management
HBR 3
Information
Recreation
Hobbies 9
Culture
Chinese 1097
English 339
Travel 31
Reference 79
Hardware 54
Computer
Hardware 259
Software
Application 213
Digitization 37
Latex 52
Manim 205
KB 1
Numeric 19
Programming
Web 289
Unicode 504
HTML 66
CSS 65
SVG 46
ASP.NET 270
OS 431
DeskTop 7
Python 72
Knowledge
Mathematics
Formulas 8
Set 1
Logic 1
Algebra 84
Number Theory 206
Trigonometry 31
Geometry 34
Calculus 67
Engineering
Tables 8
Mechanical
Rigid Bodies
Statics 92
Dynamics 37
Fluid 5
Control
Acoustics 19
Natural Sciences
Matter 1
Electric 27
Biology 1
