Content
Derivatives of Trigonometric Functions
Limits and Trigonometric Functions
Limits and Sine Function
Limits and Cosine Function
Plots of
Limits and Trigonometric Functions
Derivatives of Trigonometric Functions
Derivatives of Trigonometric Functions
Trigonometric functions are very important in practical application. Trigonmetric function f is continuous when it is defined at every real numbers x in the domain. To determine the derivatives, the real number x is the angle of the trigonometric function and is measured in radian.
Limits and Trigonometric Functions
Trigonometric functions are functions of an angle. The three basic are sine cosine and tangent. The geometric definition of trigonometric functions can be related by sides of a triangle. One important limit related to finding derivatives of trigonometric functions is the ratio of value of a trigonometric function to the angle of the trigonometric function. Geometrically, the trigonometric functions can represented by constructing triangles in a unit circle with radius r=1.
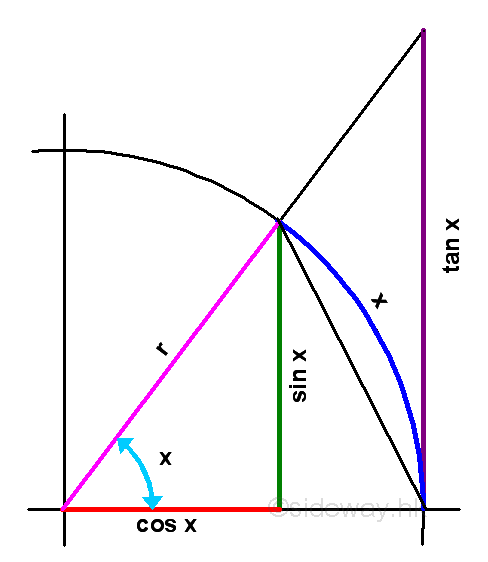
Limits and Sine Function
According to the graph, consider the angle x in radian between 0 and π/2 when x approaching zero and not equal to zero, the relationship of the area of triangle w/sin x, the area of circular sector w/arc x, and the area of triangle w/tan x are:
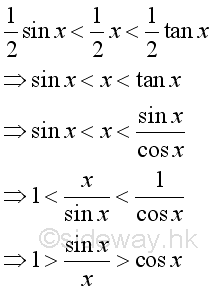
As x decrease, cos x will increase. (sin x)/x will increase also but less than 1. Imply as x approach +0, limit of (sin x)/x exists. Rearrange the inequality:
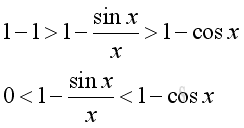
As x approach +0, i.e. δ>x>0 imply:
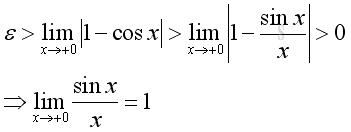
Similarly as x approach -0, imply:
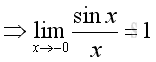
Therefore:
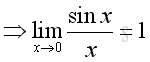
Limits and Cosine Function
Another important limit is:
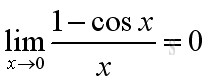
Since cosine function and sine function are related by a right angle triangle and both functions are continuous in every numbe of the domain, the cosine function can be transformed through algebraic manipulations:
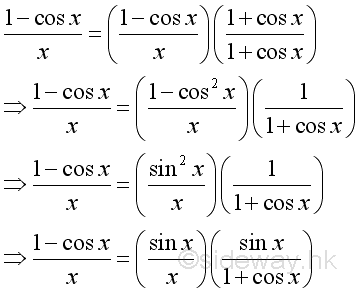
The limit of the function can be determined by:
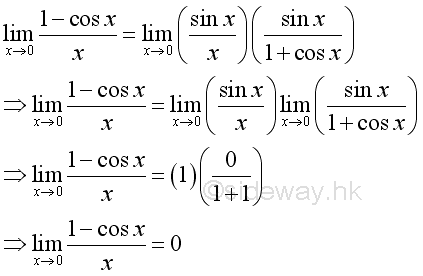
Plots of Limits and Trigonometric Functions
The inequality, limits and trigonometric functions can be plotted as in the following figure:
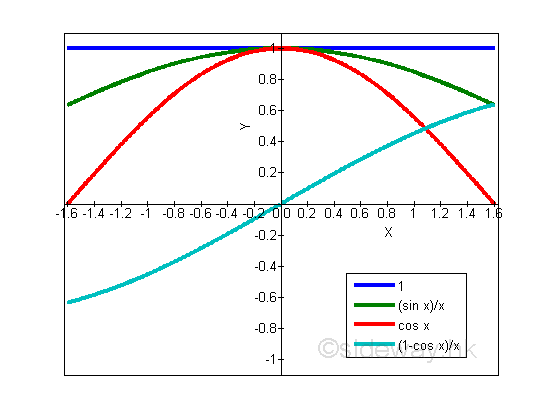
Derivatives of Trigonometric Functions
Derivative of Sine Function
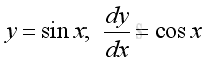
Proof:

Derivative of Cosine Function
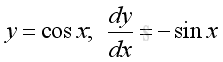
Proof:
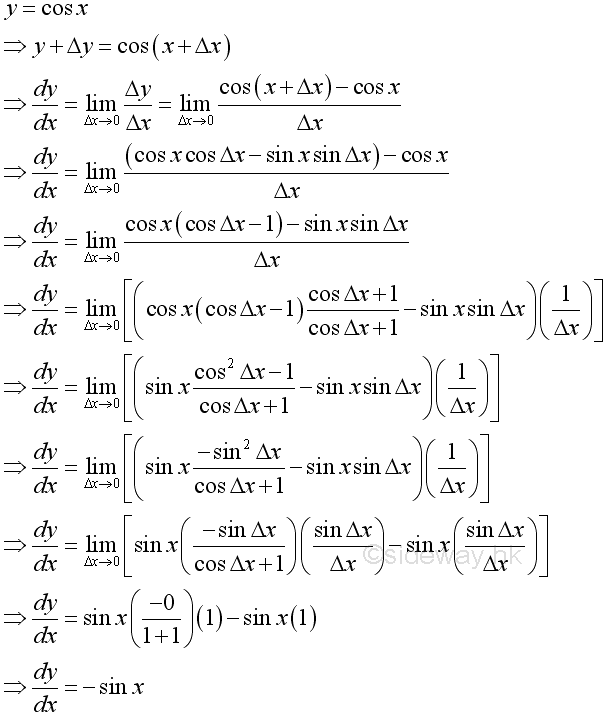
Derivative of Tangent Function
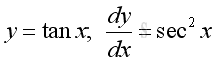
Proof:
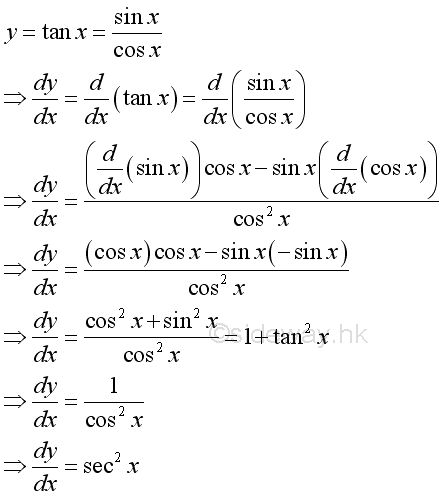
Derivative of Cotangent Function
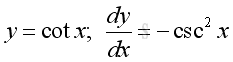
Proof:
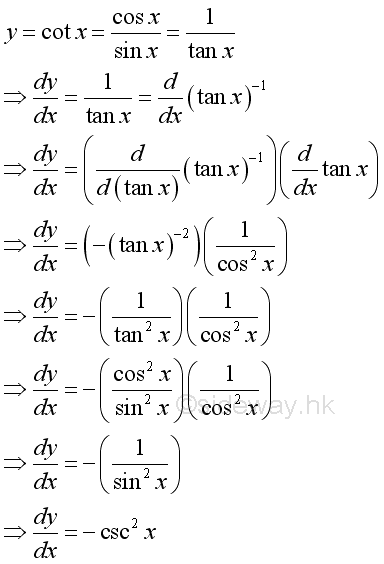
Derivative of Secant Function
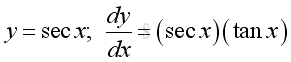
Proof:
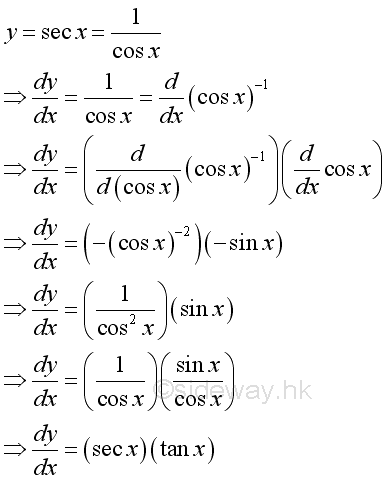
Derivative of Cosecant Function
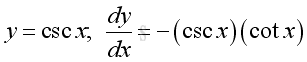
Proof:
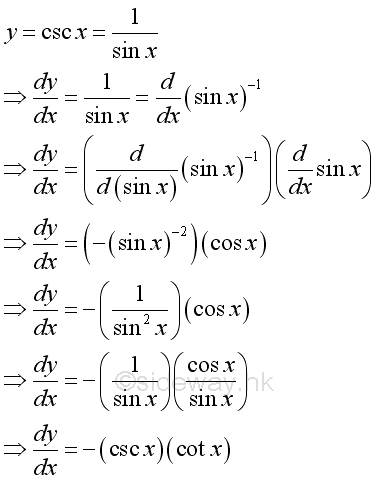
©sideway
ID: 110900006 Last Updated: 9/12/2011 Revision: 0 Ref:
References
- S. James, 1999, Calculus
- B. Joseph, 1978, University Mathematics: A Textbook for Students of Science & Engineering
Latest Updated Links
- Travel Singapore Sight(last updated On 12/6/2025)
- Travel Singapore Rail Network(last updated On 12/5/2025)
- Travel Singapore Things to Know(last updated On 12/4/2025)
- Travel Singapore(last updated On 12/3/2025)
- Legrand Galion(last updated On 12/2/2025)
- Schneider Electric AvatarOn(last updated On 12/1/2025)
- Alfalux(last updated On 11/30/2025)
- Novabell(last updated On 11/29/2025)
- TownGas NJW12RM1(last updated On 11/28/2025)
- SamSung 42" OLED TV S90F 4K(last updated On 11/27/2025)
- Tefal KI7208 GLASS VISION KETTLE(last updated On 11/26/2025)

 Nu Html Checker
Nu Html Checker  53
53  na
na  na
na
Home 5
Business
Management
HBR 3
Information
Recreation
Hobbies 9
Culture
Chinese 1097
English 339
Travel 22
Reference 79
Hardware 54
Computer
Hardware 259
Software
Application 213
Digitization 37
Latex 52
Manim 205
KB 1
Numeric 19
Programming
Web 289
Unicode 504
HTML 66
CSS 65
SVG 46
ASP.NET 270
OS 431
DeskTop 7
Python 72
Knowledge
Mathematics
Formulas 8
Set 1
Logic 1
Algebra 84
Number Theory 206
Trigonometry 31
Geometry 34
Calculus 67
Engineering
Tables 8
Mechanical
Rigid Bodies
Statics 92
Dynamics 37
Fluid 5
Control
Acoustics 19
Natural Sciences
Matter 1
Electric 27
Biology 1
