Content
Derivatives of Exponential and Logarithmic Functions
Constant e
Definition of e
Another
Definition of e
Define constant e as a sum of infinite series
Definition of
Natural Exponential Function
Derivatives of Exponential and Logarithmic Functions
Derivatives of Exponential and Logarithmic Functions
Both exponential and logarithmic functions are very important in real world problems. The natural exponential function ex has the base e. And the natural logarithmic function, ln(x) is the inverse of the natural exponential function. The constant e is an important constant in finding limits and derivatives also.
Constant e
The number e is base of the natural logarithm. The number e is a constant sometimes known as Napier's constant, named after the Scottish mathematician John Napier who introduced logarithms. The mathematical constant e is also called Euler number with its symbol honors Swiss mathematician Leonhard Euler.
The constant e is an irrational number. The numerical value of e to 10 decimal places is 2.7182818284.
Definition of e
There are many ways to define the mathematical constant e. The number e can be defined as the limit of:
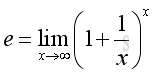
For x approaching +∞, there always exists a pair of integers such that:
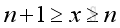
Imply:
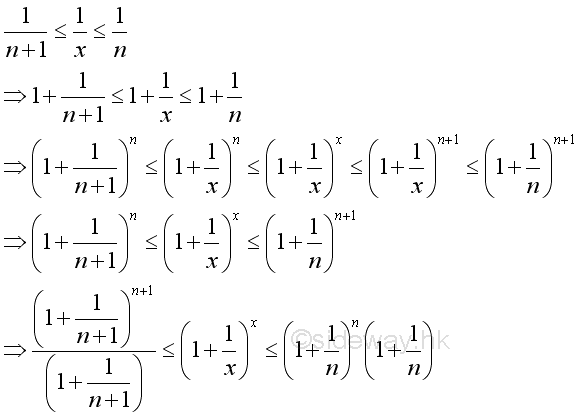
Since the following limits exist and are equal to 1:
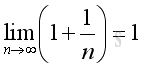 and
and
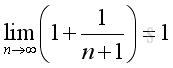
Imply:
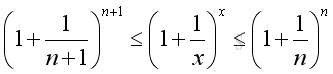
And if limits exist when n approaching +∞, that is:
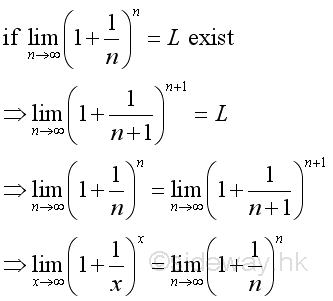
Therefore the limit when x approaching +∞ can be proved by the limit when integer n approaching +∞. And using Binomial Theorem to expand the terms in the bracket of the limit goes up to n, where n approaching +∞:
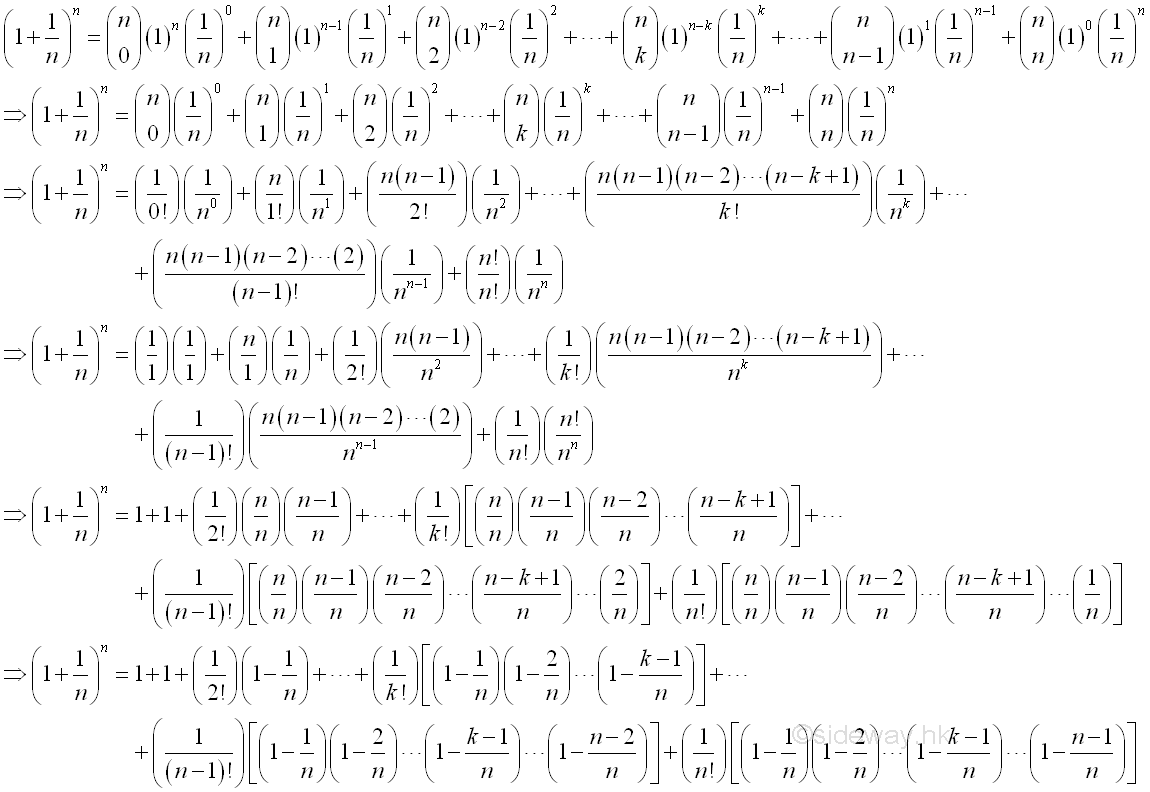
Therefore the limit when n approaching +∞ is:
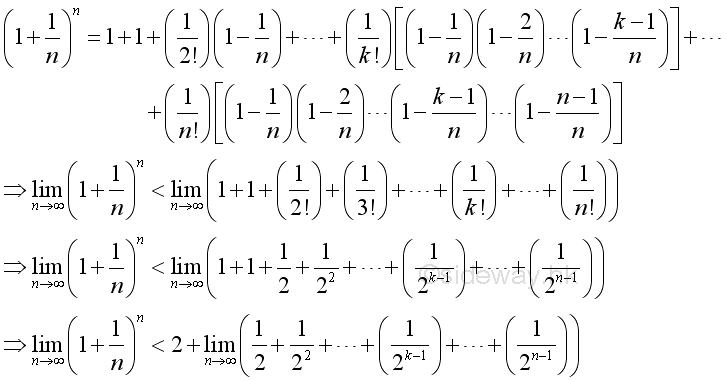
The limit on the RHS when n approaching +∞ is:
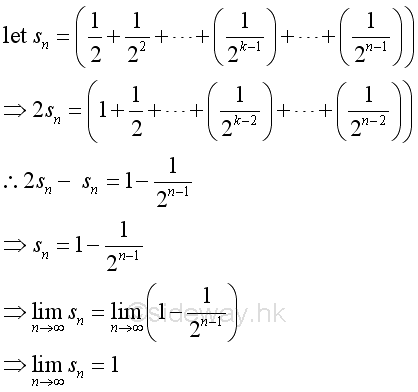
The limit on the LHS when n approaching +∞ exists:
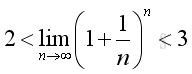
Therefore the limit of the series exists:
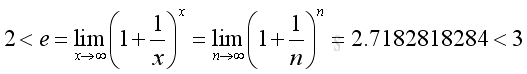
For x approaching -∞, let x=-y then:
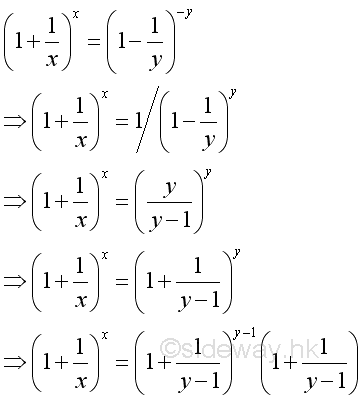
As shown before, when y approaching +∞, imply:
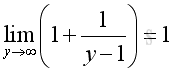 and
and
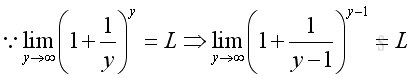
Therefore, when x approaching ∞, imply:
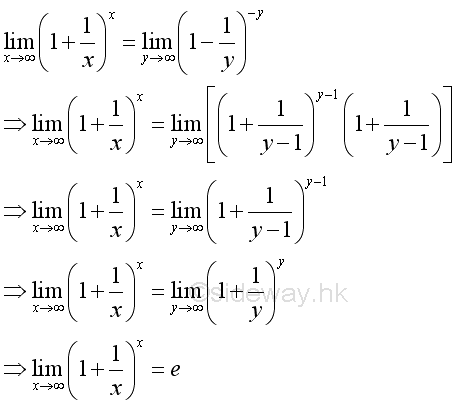
Another Definition of e
Similarly, the limit can be rewritten for x approaching 0, imply:
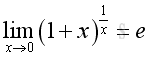
Define constant e as a sum of infinite series
Besides, as shown in the binomial expansion, the limit can also be expressed as:
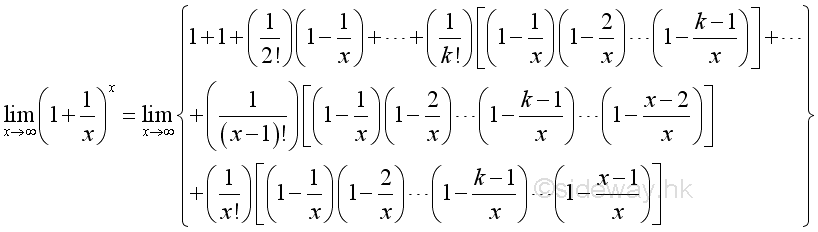
After rearrangement, imply:
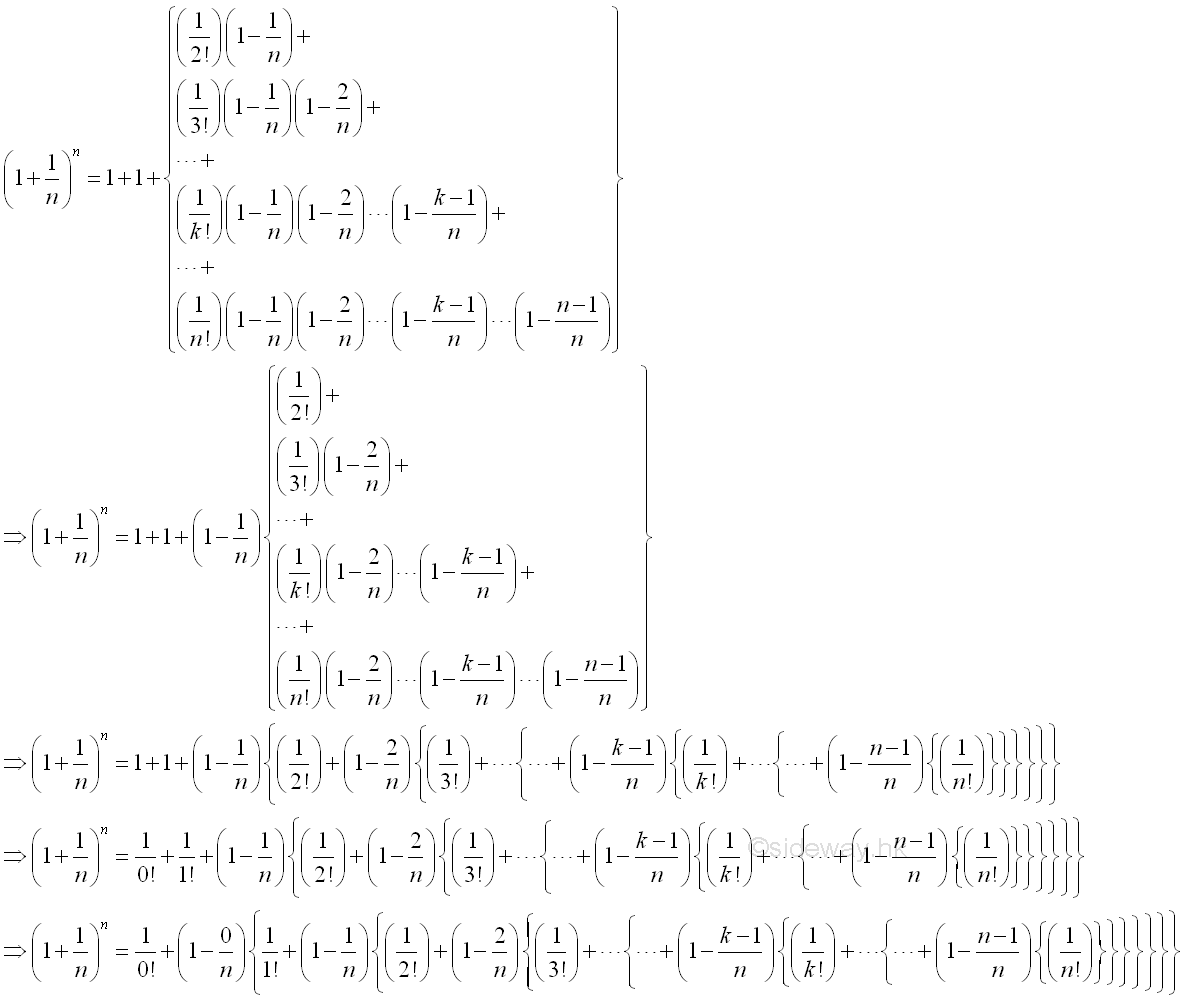
Consider the k term, when k=1:
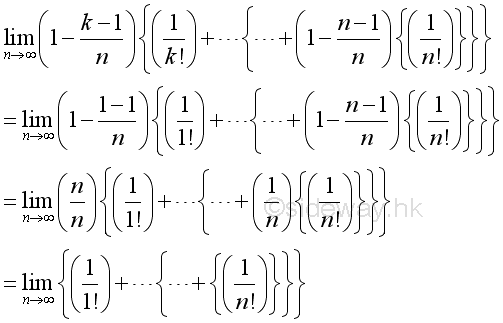
Consider the k term, when k=n-1:
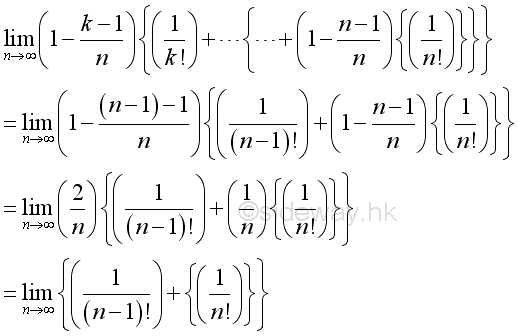
Therefore the numeric value of k term is bounded and since n approaching ∞, for every k there is a n term such that n>>k:
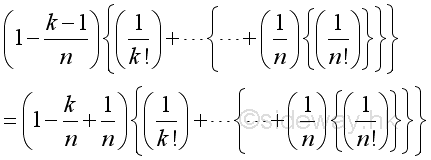
Imply when n approaching ∞, the limit of k term can be approximated by:
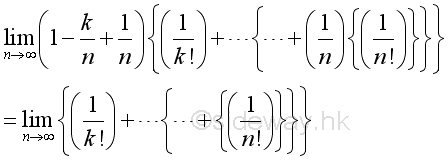
Therefore when x approaching ∞, the limit of can be approximated by:
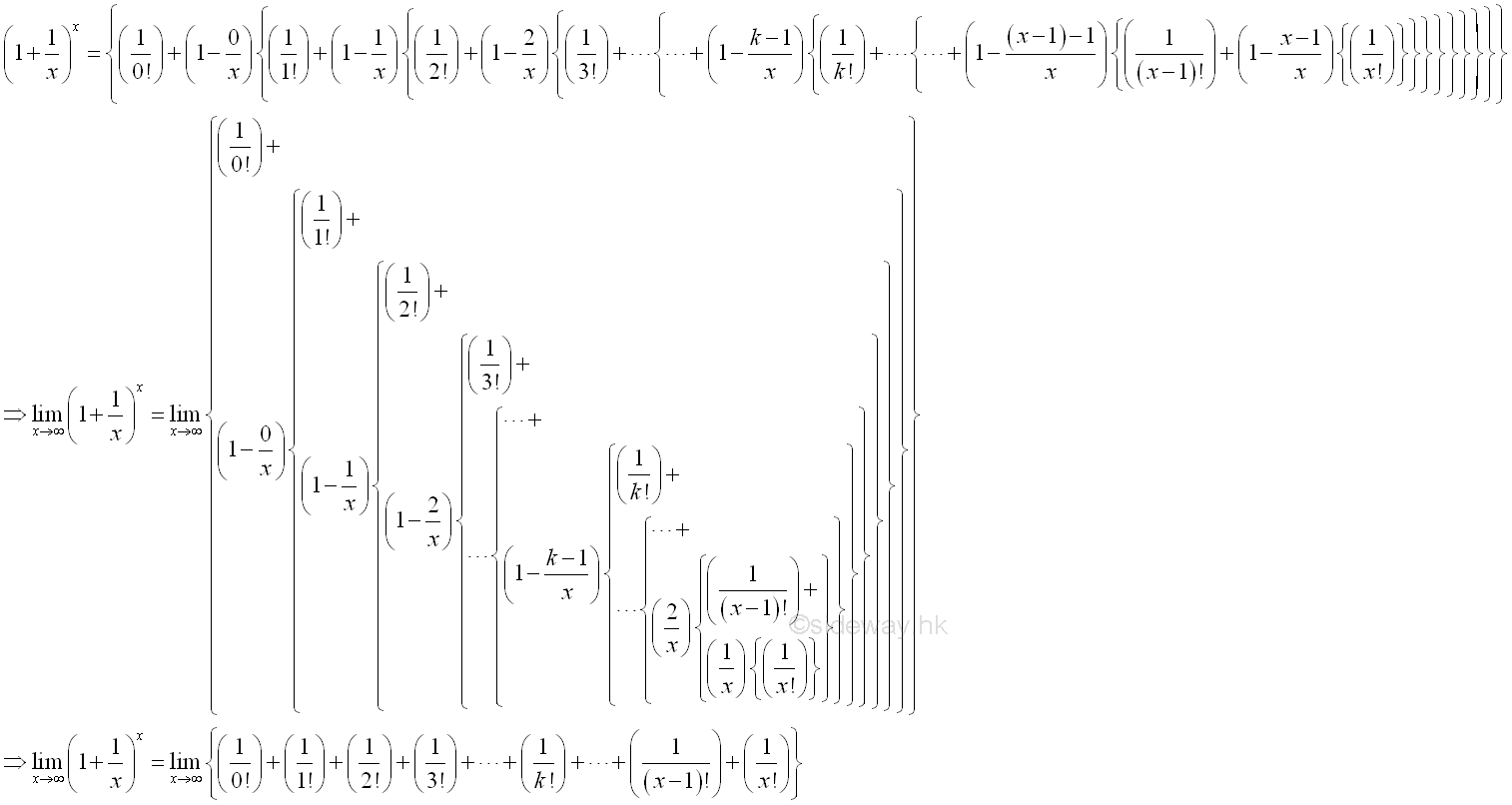
Imply:
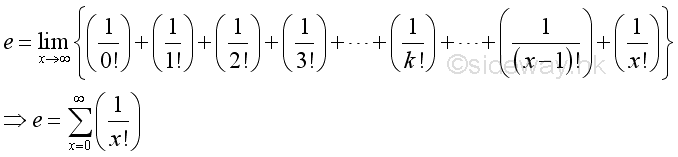
Definition of Natural Exponential Function
The Natural Exponential Function can be expressed as:
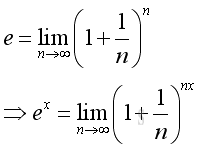
Let m=nx, since n approaching ∞, there must exist a numeric value such that m is an integer, imply:
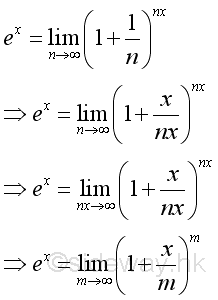
Using Binomial Theorem to expand:
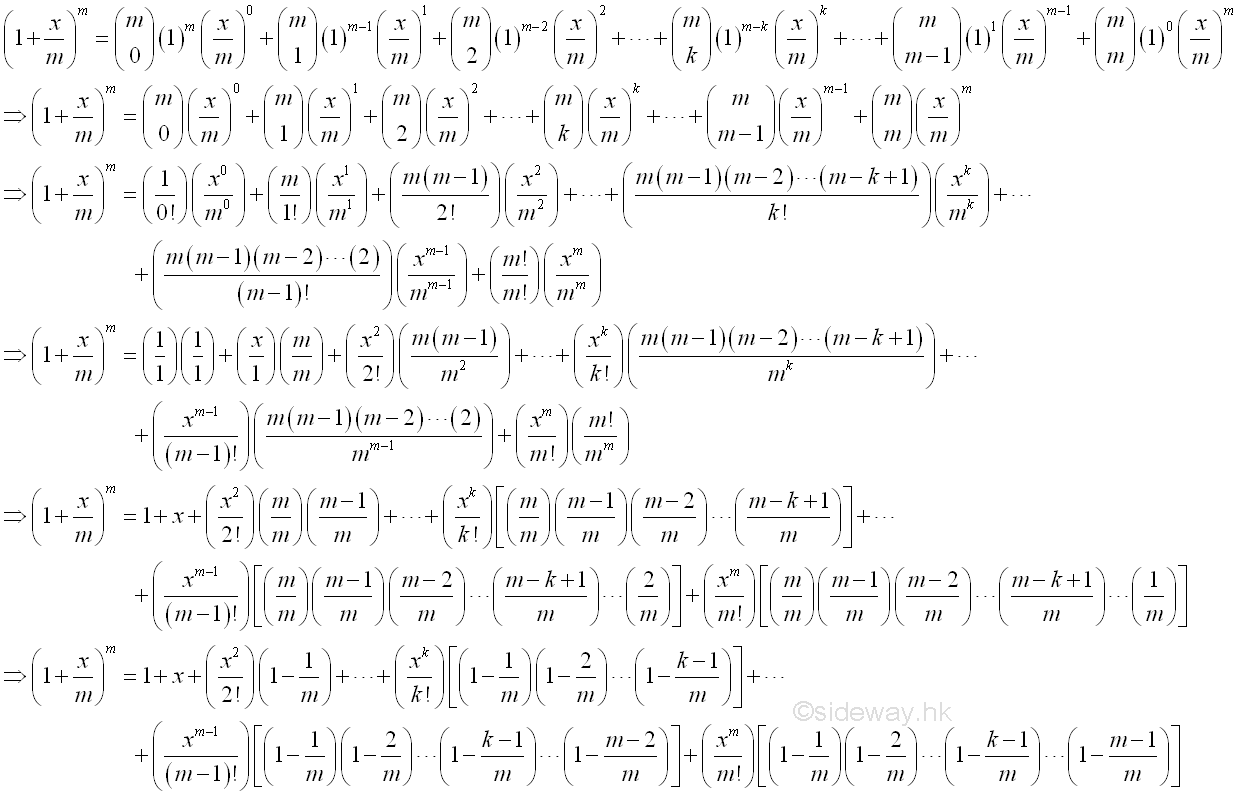
The limit is equal to :
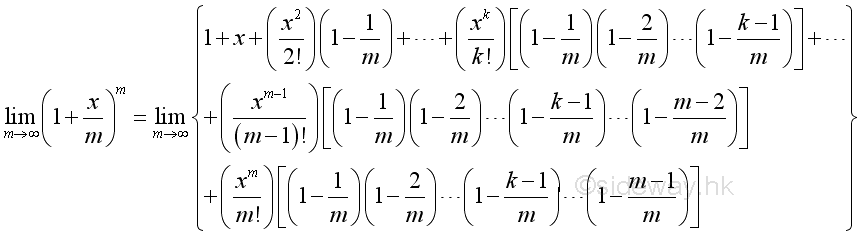
Similar to define the Euler number, the natural exponential function is equal to :
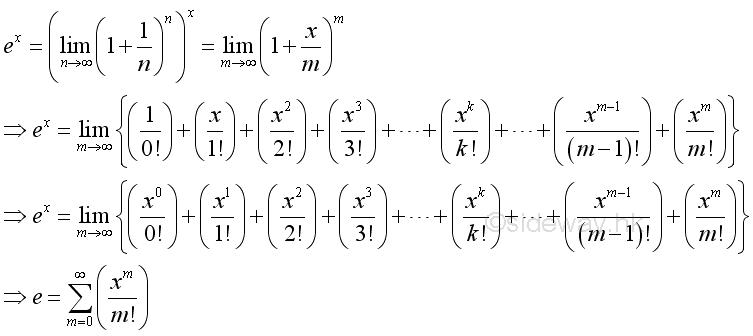
Derivatives of Exponential and Logarithmic Functions
Derivative of Natural Exponential Function
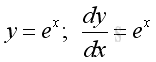
Proof:

Or:
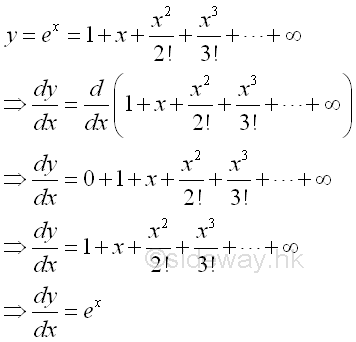
Derivative of Exponential Function

Proof:

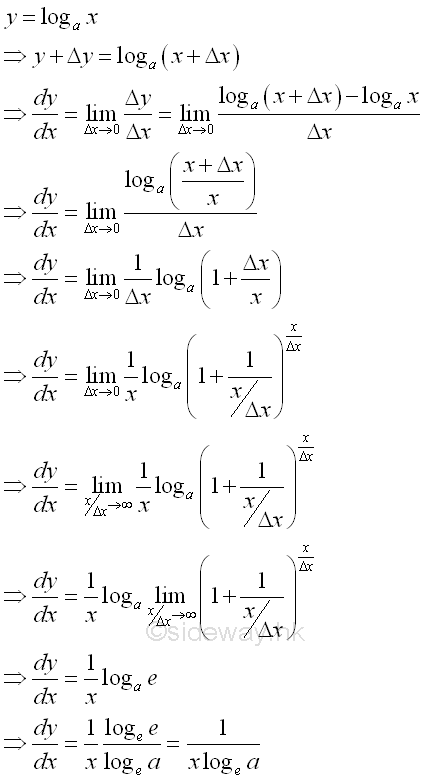
Derivative of Natural Logarithmic Function

Proof:

Proof for the power function when n is a real number:
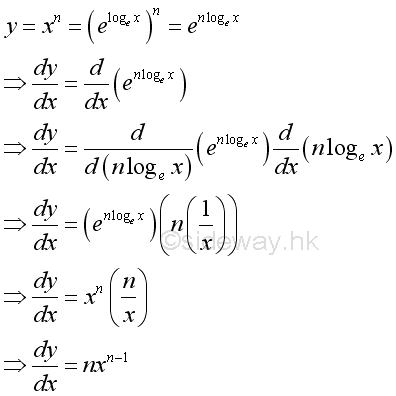
Derivative of Logarithmic Function
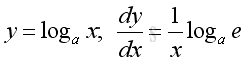
Proof:
Or:
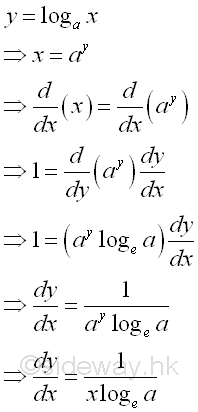
©sideway
ID: 110900007 Last Updated: 7/7/2013 Revision: 2 Ref:
References
- S. James, 1999, Calculus
- B. Joseph, 1978, University Mathematics: A Textbook for Students of Science & Engineering
Latest Updated Links
- Travel Singapore Sight West | Central(last updated On 1/6/2026)
- Travel Singapore Sight Sentosa Sensoryscape(last updated On 1/5/2026)
- Travel Singapore Sight Sentosa Resorts World Sentosa(last updated On 1/4/2026)
- Travel Singapore Sight Sentosa HarbourFront(last updated On 1/3/2026)
- Travel Singapore Sight Sentosa(last updated On 1/2/2026)
- Travel Singapore Sight River Wonders(last updated On 12/30/2025)
- Travel Singapore Sight Bird Paradise(last updated On 12/30/2025)
- Travel Singapore Sight Mandai(last updated On 12/30/2025)
- Travel Singapore Sight Rainforest Wild ASIA(last updated On 12/30/2025)
- Travel Singapore Sight Night Safari(last updated On 12/30/2025)
- Travel Singapore Sight Curiosity Cove(last updated On 12/30/2025)

 Nu Html Checker
Nu Html Checker  53
53  na
na  na
na
Home 5
Business
Management
HBR 3
Information
Recreation
Hobbies 9
Culture
Chinese 1097
English 339
Travel 37
Reference 79
Hardware 54
Computer
Hardware 259
Software
Application 213
Digitization 37
Latex 52
Manim 205
KB 1
Numeric 19
Programming
Web 289
Unicode 504
HTML 66
CSS 65
SVG 46
ASP.NET 270
OS 431
DeskTop 7
Python 72
Knowledge
Mathematics
Formulas 8
Set 1
Logic 1
Algebra 84
Number Theory 206
Trigonometry 31
Geometry 34
Calculus 67
Engineering
Tables 8
Mechanical
Rigid Bodies
Statics 92
Dynamics 37
Fluid 5
Control
Acoustics 19
Natural Sciences
Matter 1
Electric 27
Biology 1
