Content
Derivatives of Inverse Trigonometric Functions
Derivatives of
Inverse Trigonometric Functions
Derivatives of Inverse Trigonometric Functions
Inverse trigonometric functions are often found in real life applications.
Derivatives of Inverse Trigonometric Functions
Derivative of Inverse Sine Function
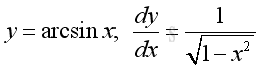
y is the angle lying between -π/2 and π/2 and x is the value of sine y from -1 to 1. The slope of the curve is always positive, imply dy/dx is alway positive.
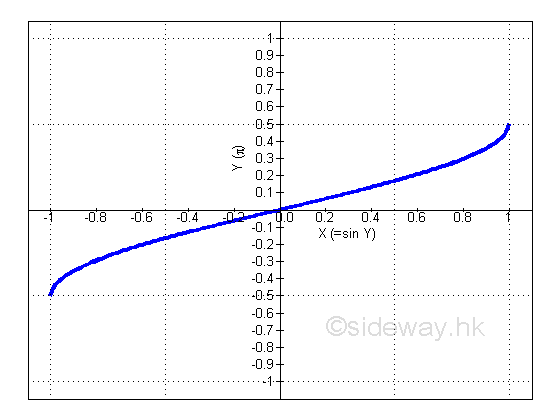
Proof:
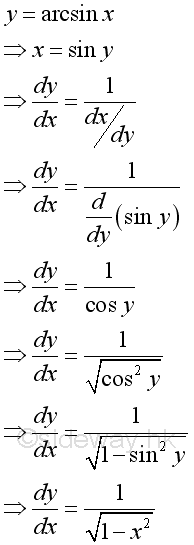
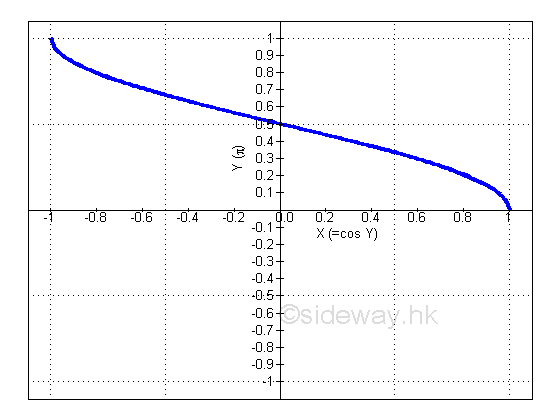
Derivative of Inverse Cosine Function
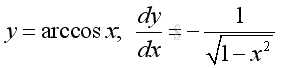
y is the angle lying between 0 and π and x is the value of cosine y from -1 to 1. The slope of the curve is always negative, imply dy/dx is alway negative.:
Proof:
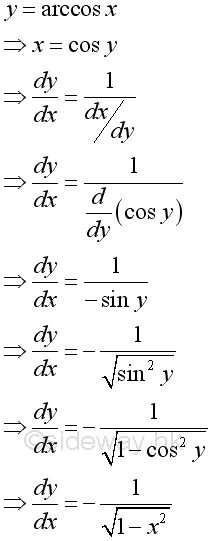
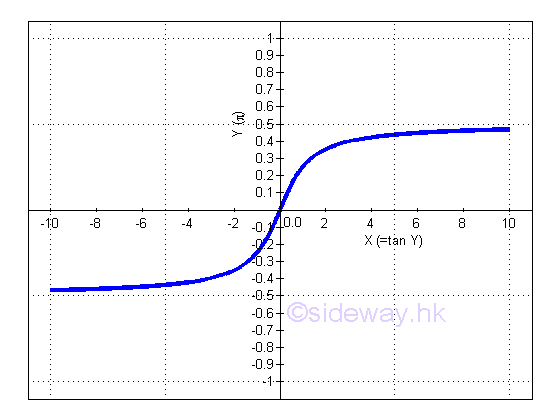
Derivative of Inverse Tangent Function
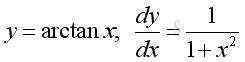
y is the angle lying between -π and π and x is the value of tangent y from -∞ to +∞. The slope of the curve is always positive, imply dy/dx is alway positive.
Proof:
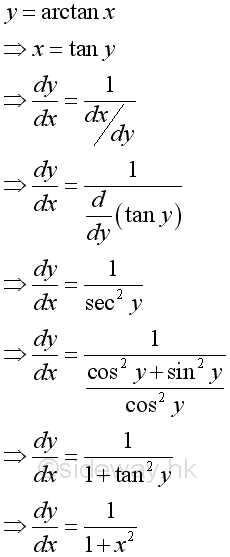
Derivative of Inverse Cotangent Function
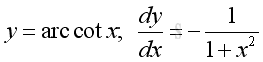
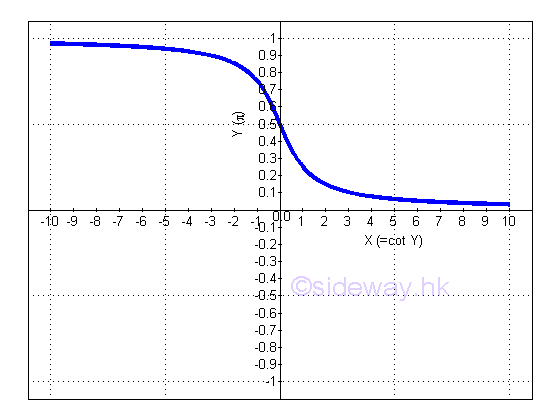
y is the angle lying between 0 and π and x is the value of cotangent y from -∞ to +∞. The slope of the curve is always negative, imply dy/dx is alway negative.:
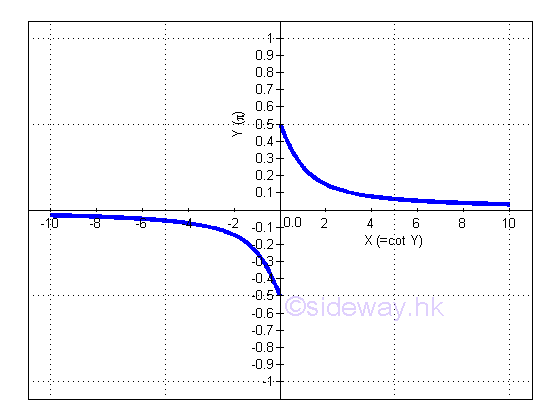
Or y is the angle lying between -π/2 and π/2 and x is the value of cotangent y from -∞ to +∞ and not equal to 0. The slope of the curve is always negative, imply dy/dx is alway negative.:
Proof:
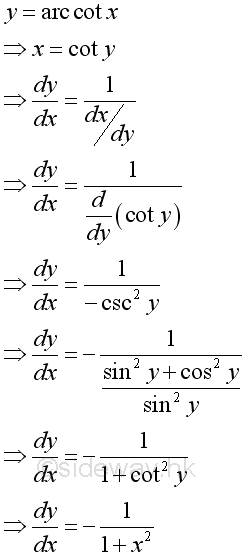
Derivative of Inverse Secant Function
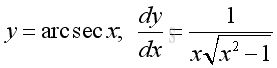
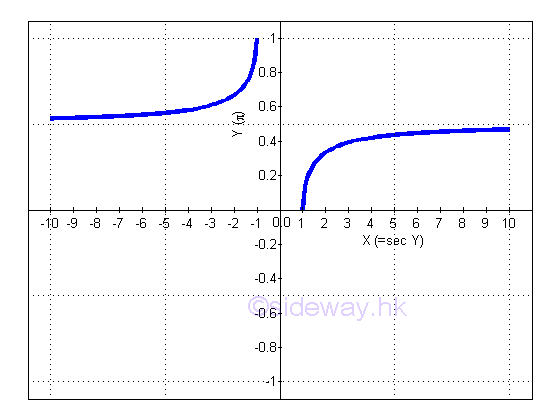
y is the angle lying between 0 and π and x is the value of tangent y from -∞ to -1 and from 1 to +∞. The slope of the curve is always positive, imply dy/dx is alway positive.
Proof:
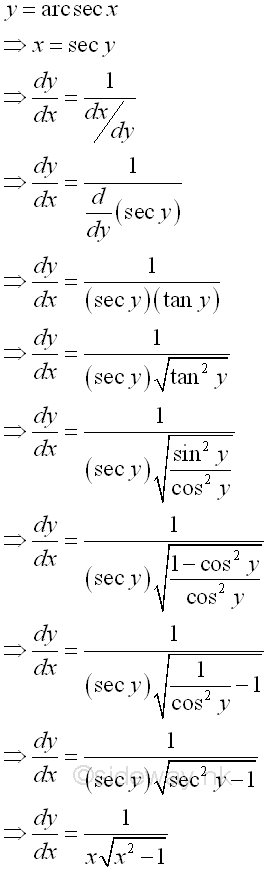
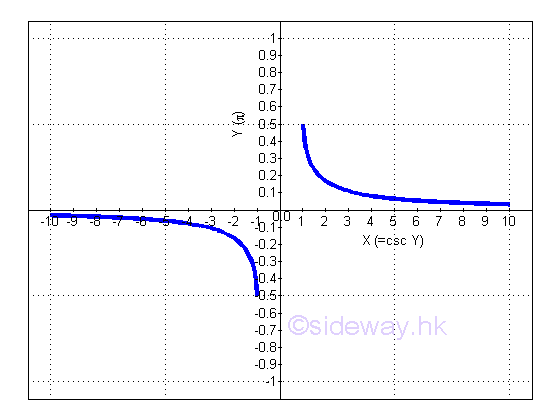
Derivative of Inverse Cosecant Function
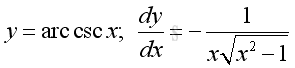
y is the angle lying between -π/2 and π/2 and x is the value of tangent y from -∞ to -1 and from 1 to +∞. The slope of the curve is always negative, imply dy/dx is alway negative.
Proof:
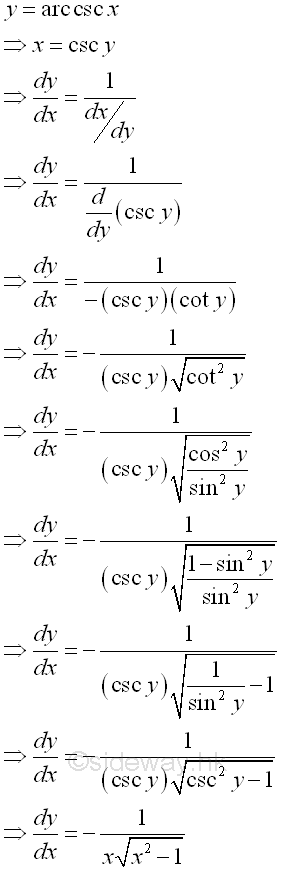
©sideway
ID: 110900008 Last Updated: 6/9/2013 Revision: 1 Ref:
References
- S. James, 1999, Calculus
- B. Joseph, 1978, University Mathematics: A Textbook for Students of Science & Engineering
Latest Updated Links
- Pentium(last updated On 7/3/2025)
- Intel CPU(last updated On 7/2/2025)
- Intel CPU History(last updated On 7/1/2025)
- FreeGLUT Windows Function(last updated On 1/27/2025)
- FreeGLUT Initialization Function(last updated On 1/26/2025)
- FreeGLUT(last updated On 1/25/2025)
- GLUT(last updated On 1/24/2025)
- OpenGL(last updated On 1/23/2025)
- XPower UC140 4-Port 140W PD3.1 GaN Travel Charger(last updated On 1/22/2025)
- XPower DX6 6 In 1 (2x3) 60W PD3.0 Sync & Charge Cable(last updated On 1/21/2025)
- XPower MF240 1.2M Magnetic Absorption 4 in 1 (2x2) Zinc Alloy 240W PD Sync & Charge Cable(last updated On 1/20/2025)

 Nu Html Checker
Nu Html Checker  53
53  na
na  na
na
Home 5
Business
Management
HBR 3
Information
Recreation
Hobbies 8
Culture
Chinese 1097
English 339
Travel 18
Reference 79
Computer
Hardware 257
Software
Application 213
Digitization 37
Latex 52
Manim 205
KB 1
Numeric 19
Programming
Web 289
Unicode 504
HTML 66
CSS 65
SVG 46
ASP.NET 270
OS 431
DeskTop 7
Python 72
Knowledge
Mathematics
Formulas 8
Set 1
Logic 1
Algebra 84
Number Theory 206
Trigonometry 31
Geometry 34
Calculus 67
Engineering
Tables 8
Mechanical
Rigid Bodies
Statics 92
Dynamics 37
Fluid 5
Control
Acoustics 19
Natural Sciences
Matter 1
Electric 27
Biology 1
