Summation of Accumulative Physical Quantity

In general, the application of integration can also be applied to other mechanical quantities by expressing the mechanical quantity in the form of accumulative mechanical quantity.

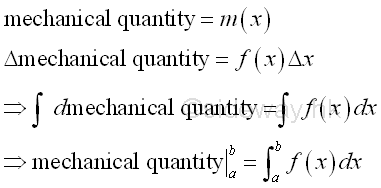
Moment of Load

Moment is a measure of the tendency of an object to rotate about a point by load. Moment can be defined as the product of a load acting upon along a line of an object and the prependicular distance between the point of action and the line of action of the load. When a beam is fixed at one end, the beam will bend downward when a load is applied on the other end. The moment at the fixed end is called bending moment

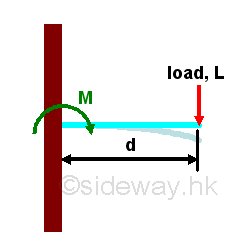
Moment of the concentrated point load at the fixed end is

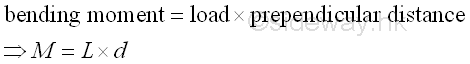
Moment of an uniformly distributed rectangular load on the beam

For an uniformly distributed rectangular load, the load is even distributed over the span of the beam, the total moment at the fixed end can be obtained by slicing the moment into infinitesimal moment elements caused by infinitesimal load elements. 

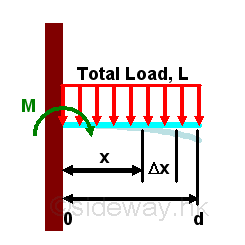
Since the load is uniformly distributed over the span of beam, the infinitesimal load element can be expressed as load per unit length, imply

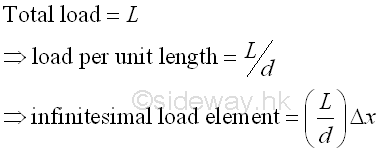
Moment of an uniformly distributed rectangular load at the fixed end of the beam is.

Moment of a non-uniformly distributed triangular load on the beam

For an non-uniformly distributed triangular load, the load is linearly distributed over the span of the beam, the total moment at the fixed end can be also obtained by slicing the moment into infinitesimal moment elements caused by infinitesimal load elements. 

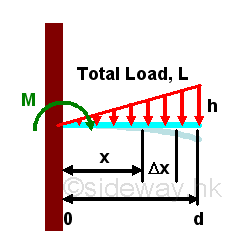
Since the load is linearly distributed over the span of beam, the infinitesimal load element can be expressed as a function of distance x from the fixed end, imply

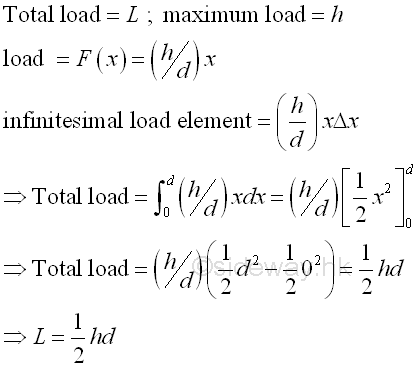
Moment of an linearly distributed triangular load at the fixed end of the beam is

Moment of a non-uniformly distributed triangular load on the beam

For an non-uniformly distributed triangular load, the load is linearly distributed over the span of the beam, the total moment at the fixed end can be also obtained by slicing the moment into infinitesimal moment elements caused by infinitesimal load elements. 

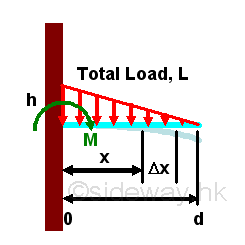
Since the load is linearly distributed over the span of beam, the infinitesimal load element can be expressed as a function of distance x from the fixed end, imply

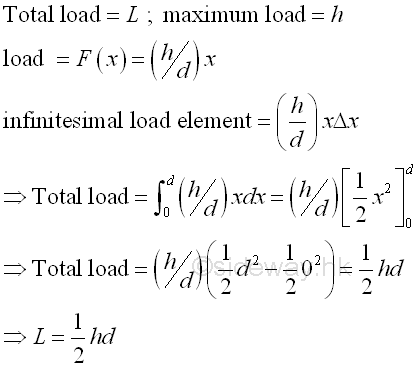
Moment of an linearly distributed triangular load at the fixed end of the beam is