Content
Centroid of 3D Body
Centroids of Volumes
Volume by Integration
Volume by Triple Integration
Centroid of 3D Body
The centroid of 3D Body is determined by the first moment of a three dimensional body with the method of the first moment of volume.
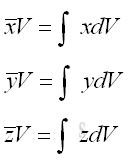
Centroids of Volumes
Volume by Integration
Volume by Triple Integration
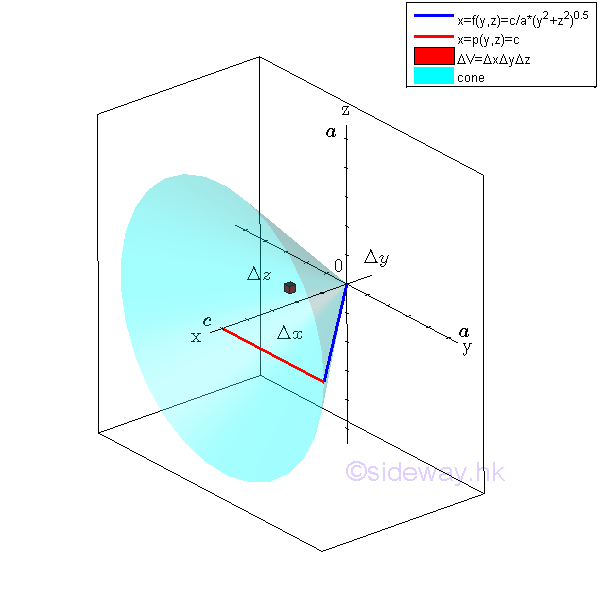
For example, the signed volume of the 3D region U is bounded by surfaces in rectangular form , Imply
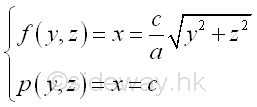
An elemental volume ΔV in rectangular form can be defined as Δx times Δy times Gz. Imply
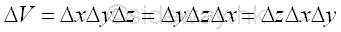
Therefore the volume of the solid cone U in cartesian coordinates xyz is equal to
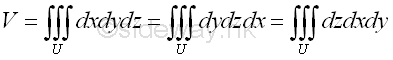
In general, the volume of a region can be determined by multiple integration through sweeping the signed elemental volume starting from along any one of the rectangular coordinate axes. Imply
Starting from horizontal sweeping along x axis

Considering an elemental volume along x axis. Imply
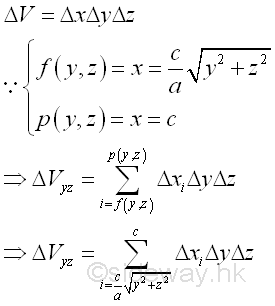
All elemental volumes can be bounded by curves in the plane yz. And the curves is
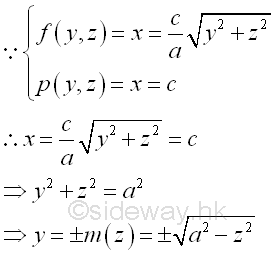
Similarly sweeping the elemental volume ΔVyz along y axis horizontally.
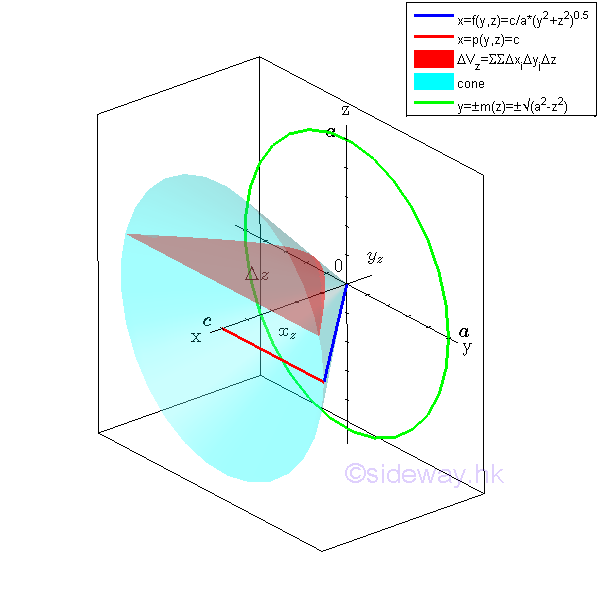
Considering an elemental volume ΔVz along y axis. Imply
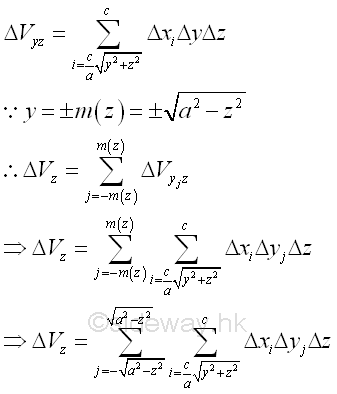
Since the bounding curves are joined at plane zx, The bounds of the bounding curves are
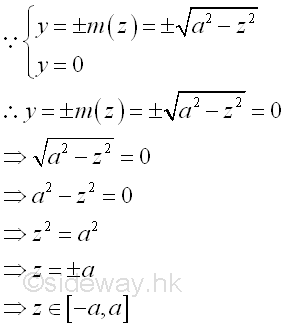
Therefore the volume of the solid cone U is
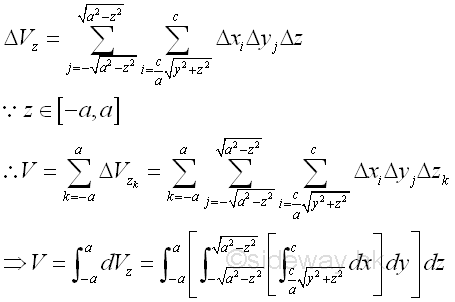
The volume of the solid cone U can also be determined starting from other axis.
Starting from horizontal sweeping along y axis
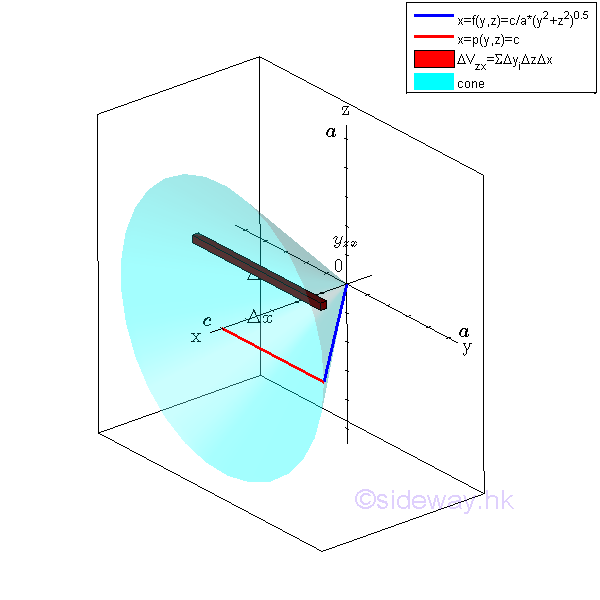
Considering an elemental volume along y axis. Imply
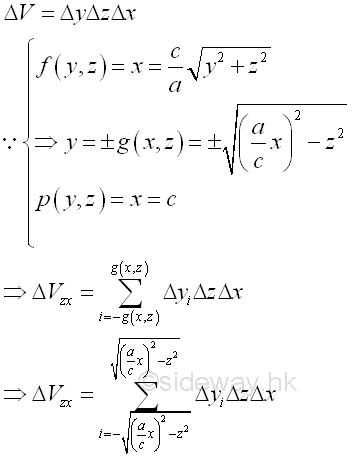
All elemental volumes in z direction can be bounded by curves in the plane zx. And the curves is
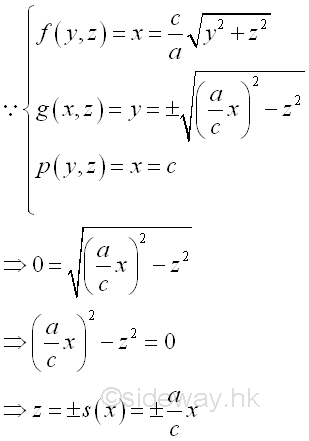
Similarly sweeping the elemental volume ΔVzx along z axis vertically.
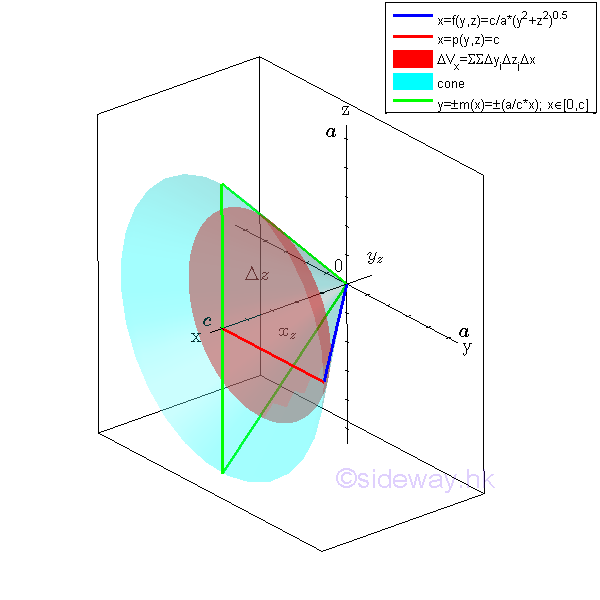
Considering an elemental volume ΔVx along z axis. Imply
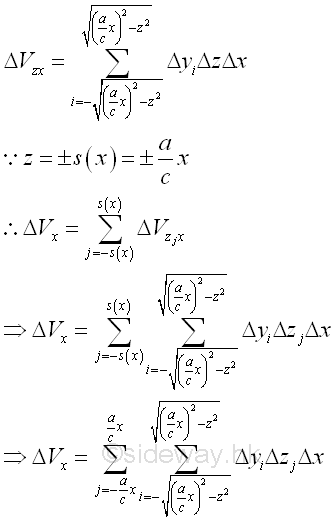
The bounding curves in x direction can also be bounded at plane zx. The bounds of the bounding curves are
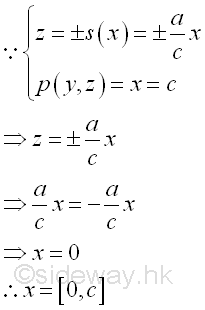
The volume of the solid cone U can be expressed as
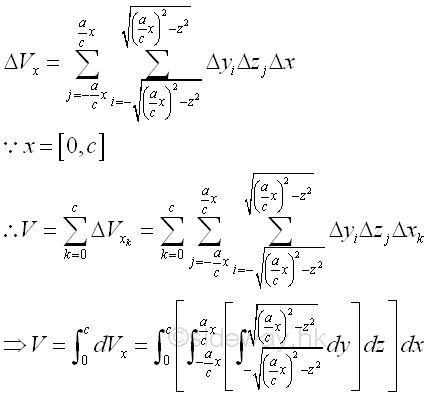
Therefore the volume of the solid cone U is
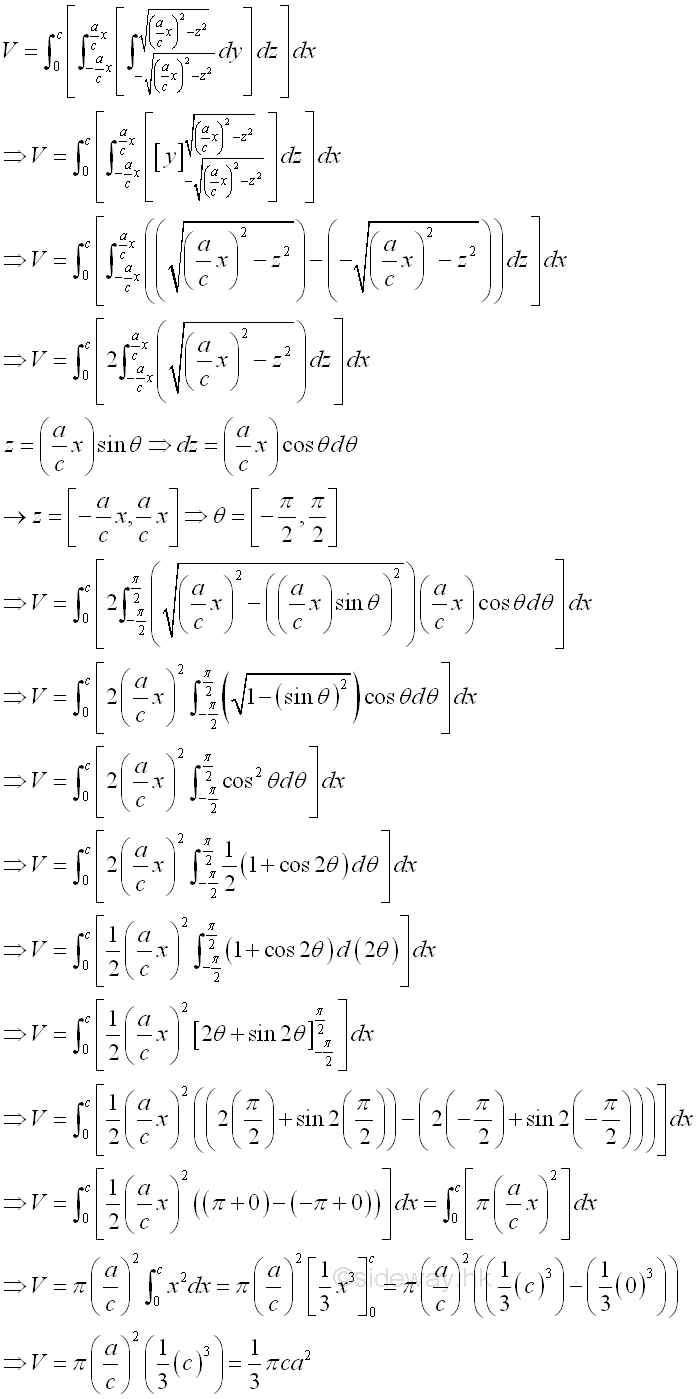
©sideway
ID: 120600011 Last Updated: 6/21/2012 Revision: 0 Ref:
References
- I.C. Jong; B.G. rogers, 1991, Engineering Mechanics: Statics and Dynamics
- F.P. Beer; E.R. Johnston,Jr.; E.R. Eisenberg, 2004, Vector Mechanics for Engineers: Statics
Latest Updated Links
- Travel Singapore Sight Mandai(last updated On 12/8/2025)
- Travel Singapore Sight Bird Paradise(last updated On 12/7/2025)
- Travel Singapore Sight(last updated On 12/6/2025)
- Travel Singapore Rail Network(last updated On 12/5/2025)
- Travel Singapore Things to Know(last updated On 12/4/2025)
- Travel Singapore(last updated On 12/3/2025)
- Legrand Galion(last updated On 12/2/2025)
- Schneider Electric AvatarOn(last updated On 12/1/2025)
- Alfalux(last updated On 11/30/2025)
- Novabell(last updated On 11/29/2025)
- TownGas NJW12RM1(last updated On 11/28/2025)

 Nu Html Checker
Nu Html Checker  53
53  na
na  na
na
Home 5
Business
Management
HBR 3
Information
Recreation
Hobbies 9
Culture
Chinese 1097
English 339
Travel 24
Reference 79
Hardware 54
Computer
Hardware 259
Software
Application 213
Digitization 37
Latex 52
Manim 205
KB 1
Numeric 19
Programming
Web 289
Unicode 504
HTML 66
CSS 65
SVG 46
ASP.NET 270
OS 431
DeskTop 7
Python 72
Knowledge
Mathematics
Formulas 8
Set 1
Logic 1
Algebra 84
Number Theory 206
Trigonometry 31
Geometry 34
Calculus 67
Engineering
Tables 8
Mechanical
Rigid Bodies
Statics 92
Dynamics 37
Fluid 5
Control
Acoustics 19
Natural Sciences
Matter 1
Electric 27
Biology 1
