Content
Principal Moments of Inertia
Product of Inertia
Parallel-Axis Theorem of Product of Inertia
Example of Product Moment of Inertia of a Right Angle Triangle
Product Moment of Inertia of a Right Angle Triangle by Double Integration
Product Moment of Inertia of a Right Angle Triangle by Parallel-axis Theorem
Principal Axes and Principal Moments of Inertia
Transformation of Moments of Inertia
Principal Axes of Moments of Inertia
Principal Moments of Inertia
Principal Moments of Inertia
One of the major interest in the moment of inertia of area A is determining the orientation of the orthogonal axes passing a pole on the area with maximum or minimum moment of inertia about the axes.
Product of Inertia
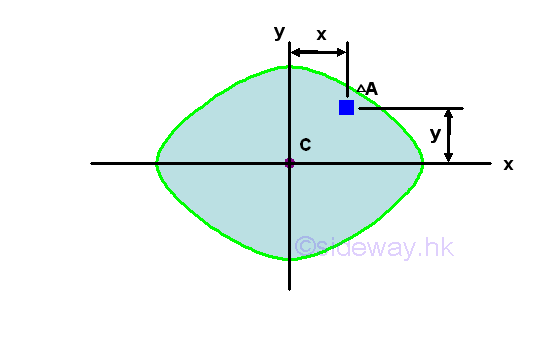
Similar to the moment of inertia, a product of inertia can also be obtained from an integral over an area by multiplying the product of the coordinates x and y about the reference coordinate axes by the elemental area. Imply
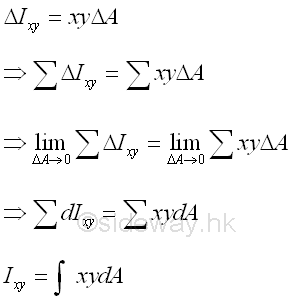
When considering the second moment of an area as the effect of the first moment acting on the same reference axis, the product moment of an area can be considered as the cross effect of the first moment acting on the orthogonal axis through a origin O at the specified orientation with respect to the area A.
Unlike the moment of inertia, although the elemental area is positive, the product of inertia can be positive, negative, or zero because the value of the coordinates x and y can be positive, negative, or zero. Similar to the first moment of an area about the the axis of symmetry, when one or both of the coordinate axes, x and y are the axis of symmetry of the area A, the integral, the product of inertia Ixy about the coordinate axes is zero. For example, a symmetrical area,
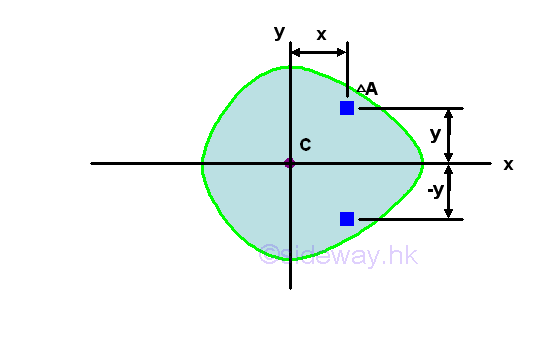
Although the area A is not symmetrical about axis y, however since the area is symmetrical about axis x, for any elemental area at a distance y above the axis x, there is always an elemental area below the axis x at the same mirror location of distance -y below the axis x. Therefore the product of inertia of a paired elemental area will cancel out each other and becomes zero, and the integral will reduces to zero also. Imply
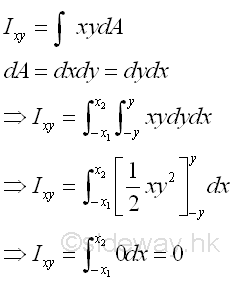
Since the product of inertia of a symmetrical area about one or two axes of symmetry must be zero, the product of inertia of an area with respect to axes can be used to test the dissymmetry or imbalance of the area about x and y axes because when the product of inertia about x and y axes is not equal to zero, the area is not symmetrical about both x and y axes. But when the product of inertia about x and y axes is equal to zero, the area may be not symmetrical about x and y axes.
Parallel-Axis Theorem of Product of Inertia
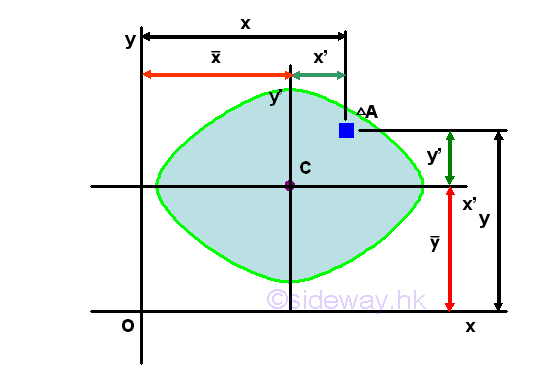
Assume axes x and y are the interested rectangular coordinate axes and axes x' and y' are the two rectangular centroidal axes of the area parallel to the coordinate axes respectively. Using axes x and y as the system coordinate, the coordinate of the centroid C can be denoted by x and y accordingly and the coordinate of the elemental area can be denoted by x and y respectively. Therefore the location (x,y) of the elemental area can also be expressed in terms of the coordinate (x,y) of the centroid C as derived in the parallel-axes theorem for the second moment of an area. Imply
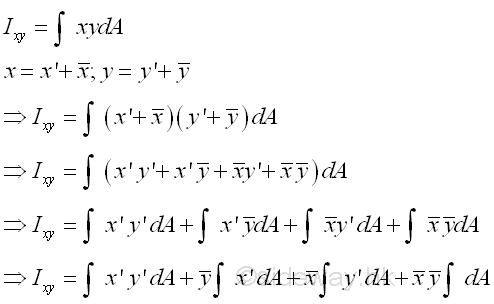
The first integral is the product of inertia Ix'y' of the area A about the centroidal axes, x' and y' . The second an third integrals are the first moment of the area A about the centroidal axes, x' and y' and the value of the first moment of the area about the centroidal axis is equal to zero. The fourth integral is equal to the total area only. Imply
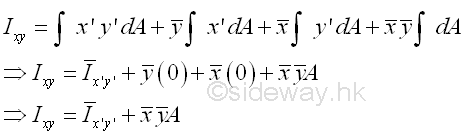
Similarly, both the coordinate (x,y) of centroid C of the area A and the coodinate (x',y') of the elemental area dA can be posititve, negative and zero, the product of inertia Ixy can therefore also be posititve, negative and zero.
Example of Product Moment of Inertia of a Right Angle Triangle
Product Moment of Inertia of a Right Angle Triangle by Double Integration
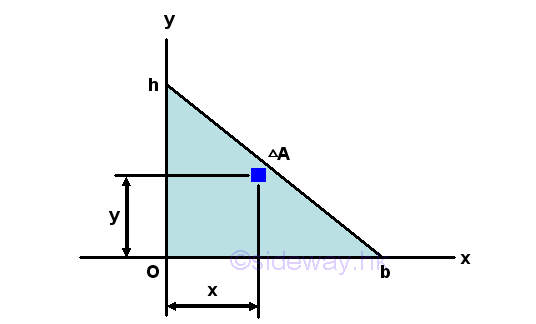
The product moment of an area A of a right angle triangle about the axes xy is
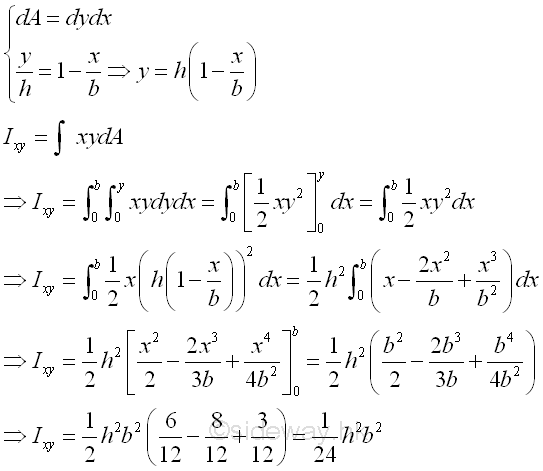
Product Moment of Inertia of a Right Angle Triangle by Parallel-axis Theorem
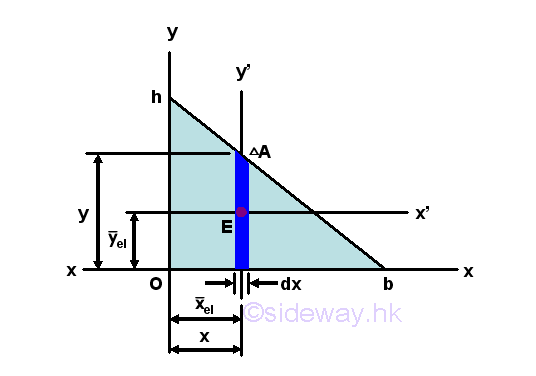
Assuming the elemental area is a rectangular area, the product moment of an elemental area dA of a right angle triangle about the centroidal axes x'y' is
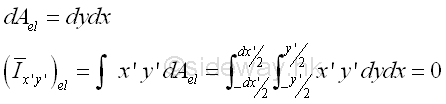
The product moment of an elemental area dA of a right angle triangle about the centroidal axis xy is
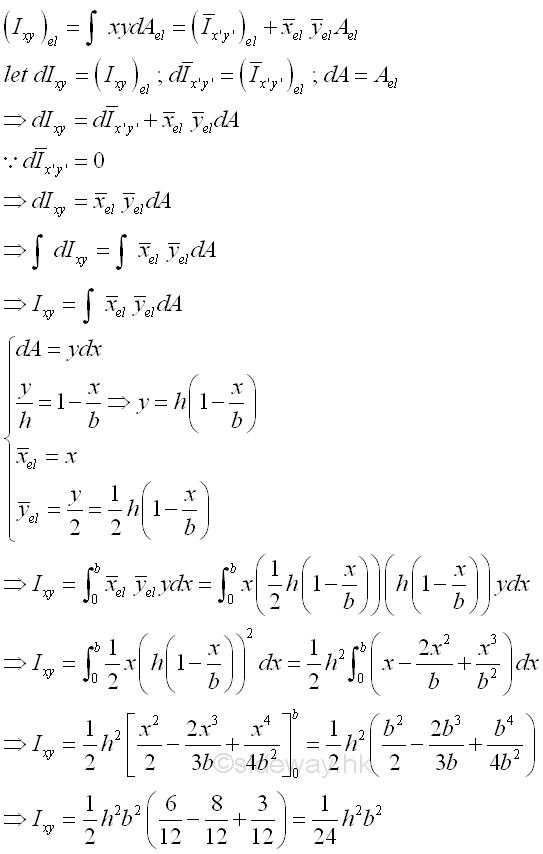
Principal Axes and Principal Moments of Inertia
Transformation of Moments of Inertia
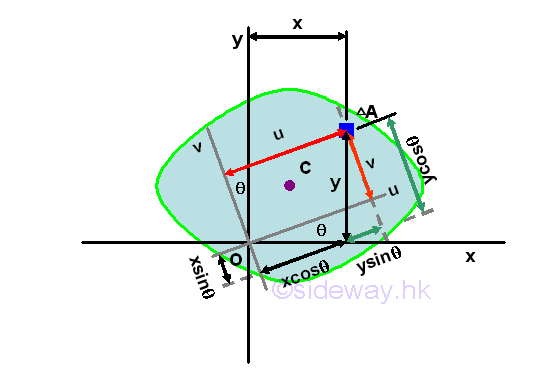
In general, the rectangular moments and product of inertia about the rectangular coordinate system at the pole O is depending on the orientation of the rectangular reference axes of which the rectangular moments and product of intertia with respect to. Consider an area A is located in a plane with a system of rectangular coordinate, x and y through the pole O, the rectangular moments and product of inertia of the area A with respect to the axes, x and y are
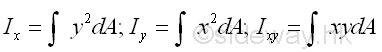
A new rectangular coordinate axes u and v can be obtained by rotating the rectangular coordinate axes x and y about the pole O by an angle θ. The moments and product of inertia of the area A with respect to the new axes, u and v are
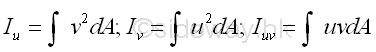
The coordinates of the elemental area on the two rectangular coordinate systems can be related by the rotating angle θ. Imply
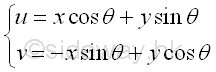
If Ix, Iy and Ixy are known, then

Since the polar moment of inertia about the origin is equal to the sum of paired rectangular moments of inertia. Imply
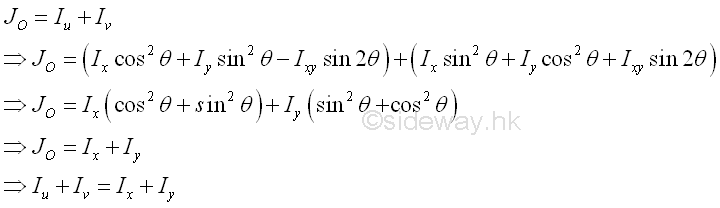
Principal Axes of Moments of Inertia
Therefore the sum of paired rectangular moments of intertia about a pole is alway a constant regardless of the orientation of the coordinate axes. Since the rectangular moment is a funtion of angle θ, a maximum or a minimum value can be obtained by differentiating either one of the rectangular moments of inertia. Imply
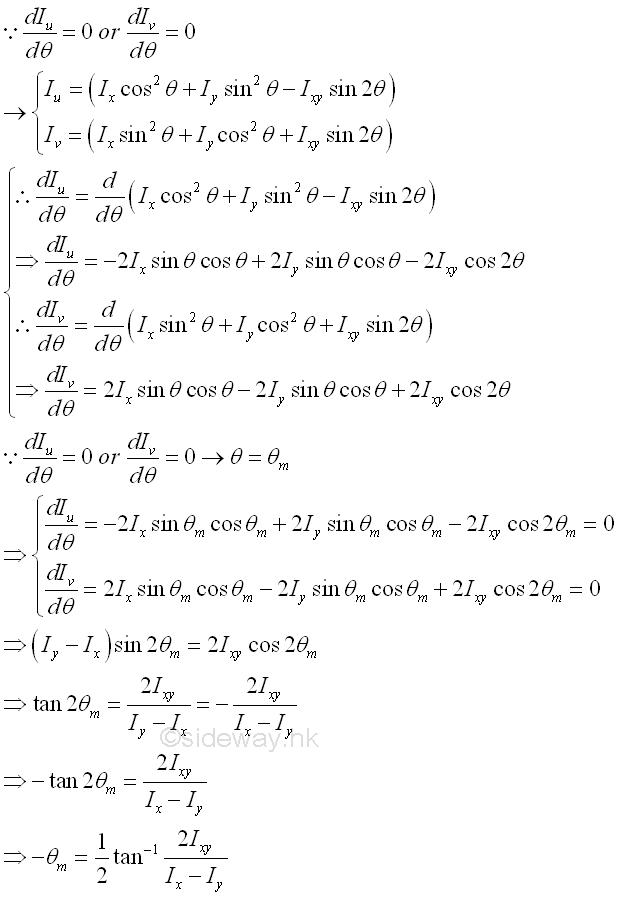
Through differentiation, the angle θ of the rectangular coordinate axes, at which the rectangular moments of inertia is either maximum or minimum, can be determined. These paired rectangular coordinate axes is called principal axes and the paired rectangular moments of inertia is called principal moments of inertia. The origin O of the rectangular coordinate axes can be located inside or outside the area, if the origin O chosen is coincide with the centroid, the two principal axes of the area about the axes through its centroid C are called the principal centroidal axes of the area. Since a tangent function is a periodic function with period π, the equation defines two values 2θm of 180o apart and the two values of θm are 90o apart which is confirmed with the maximum and minimum values of rectangular moments of inertia about the rectangular coordinate axes, i.e. the principal moments of inertia about O. Imply
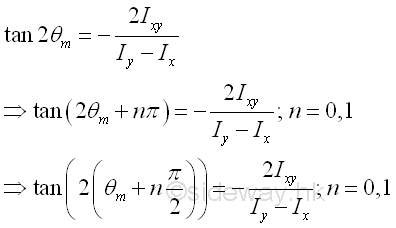
Principal Moments of Inertia
Besides, one more relation between the rectangular moments of inertia and the product of inertia at the principal axes is obtained. The product of inertia with respect to the principal axes can also be determined. Imply
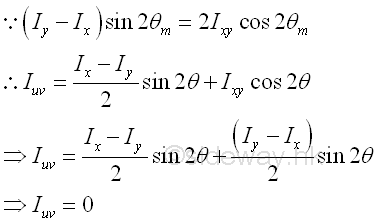
Therefore the product of inertia on the principal axes is equal to zero. Since the product of inertia is also equal to zero if one or both of the rectangular axes is an axis of symmetry of the area and is independent on the location of the origin O, an axis of symmetry is a principal axis, but a principal axis may not be an axis of symmetry. Since the product of inertia is equal to zero, the rectangular principal moments of an area can be expressed as

Besides the sum of the rectangular moments of inertia Ix and Iy is an invarient of the system. The group terms of value square of R is also an invarient under the rotation of the rectangular coordinate axes. Imply
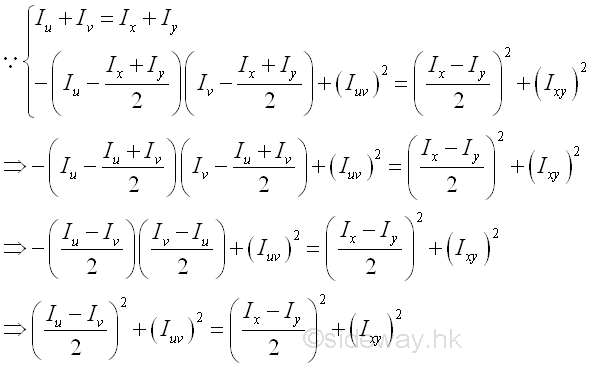
Or in an alternate form. Imply
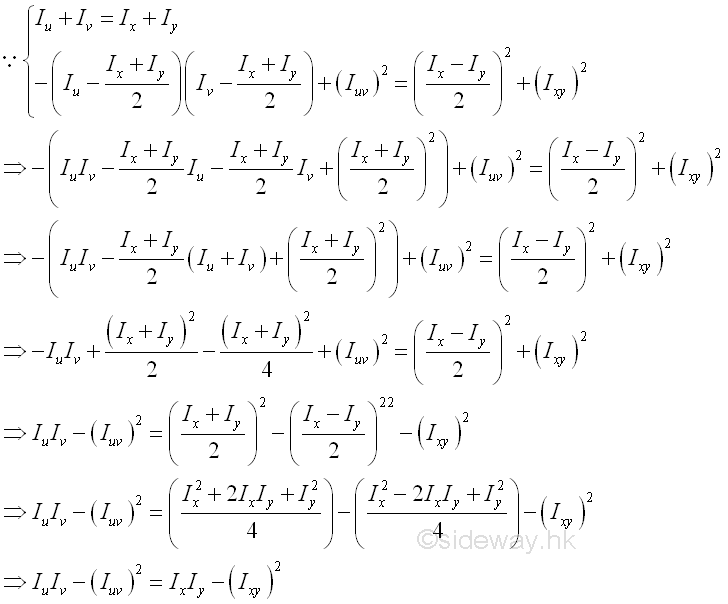
The group terms on the left hand side of value the product of rectangular moments of inertia minus the square of product of inertia is also an invarient under the rotation of the rectangular coordinate axes.
©sideway
ID: 121000010 Last Updated: 11/16/2012 Revision: 1 Ref:
References
- I.C. Jong; B.G. rogers, 1991, Engineering Mechanics: Statics and Dynamics
- F.P. Beer; E.R. Johnston,Jr.; E.R. Eisenberg, 2004, Vector Mechanics for Engineers: Statics
Latest Updated Links
- Ikea SANDSBERG table(last updated On 11/4/2025)
- Ikea TISKEN toilet roll holder(last updated On 11/3/2025)
- Philips CL400 Ceiling Light 36W(last updated On 11/2/2025)
- Philips CL400 Ceiling Light 24W(last updated On 11/1/2025)
- Philips CL400 Ceiling Light 13W(last updated On 10/30/2025)
- Ikea TISKEN basket(last updated On 10/29/2025)
- Ikea TISKEN towel rack(last updated On 10/28/2025)
- Ikea REXBEGONIA mattress protector(last updated On 10/27/2025)
- Ikea KEJSAROLVON mattress protector(last updated On 10/26/2025)
- Ikea KVARNVEN ergonomic pillow(last updated On 10/25/2025)
- Ikea BRUKSVARA pocket prung mattress(last updated On 10/24/2025)

 Nu Html Checker
Nu Html Checker  53
53  na
na  na
na
Home 5
Business
Management
HBR 3
Information
Recreation
Hobbies 8
Culture
Chinese 1097
English 339
Travel 18
Reference 79
Hardware 27![]()
Computer
Hardware 259
Software
Application 213
Digitization 37
Latex 52
Manim 205
KB 1
Numeric 19
Programming
Web 289
Unicode 504
HTML 66
CSS 65
SVG 46
ASP.NET 270
OS 431
DeskTop 7
Python 72
Knowledge
Mathematics
Formulas 8
Set 1
Logic 1
Algebra 84
Number Theory 206
Trigonometry 31
Geometry 34
Calculus 67
Engineering
Tables 8
Mechanical
Rigid Bodies
Statics 92
Dynamics 37
Fluid 5
Control
Acoustics 19
Natural Sciences
Matter 1
Electric 27
Biology 1
