Content
Second Moment of Mass
Moment of Inertia of a Thin Plate
Moment of Inertia of
Thin Circular Plate
Moment of Inertia of
Thin
Rectangular Plate
Second Moment of Mass
Similarly, the second moment of mass about an axis is equal to the summation of the products of the square of the distance between the elemental mass and the reference axis, and the elemental mass over an area. As the second moment of mass is usually refered to the rotation, the distance between the elemental mass and the rotating axis is denoted by r. Imply
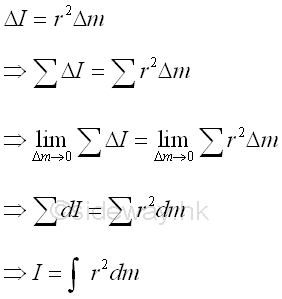
Moment of Inertia of a Thin Plate
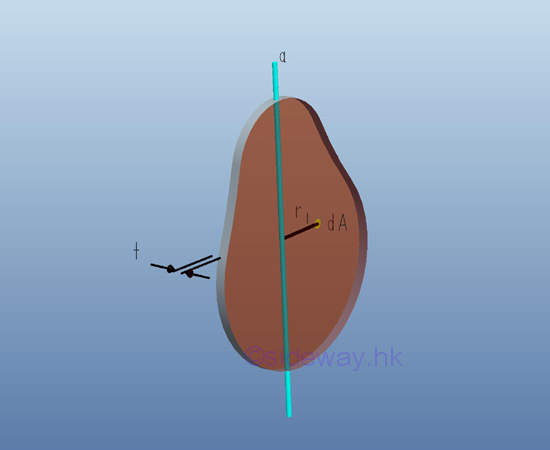
Consider a thin plate of area A with uniform thickness t and homogenouse material density ρ. Both the thickness and the material density are constant over the area. Since the thickness t is much smaller than the plate dimension, the mass and the elemental mass of the thin plate can be expressed in terms of the thickness and the material density, if the reference axis lies in the middle plane of the plate, the mass moment of inertia of the thin plate with respect to an axis can be expressed as the elemental area on the middle plane with the distance r as the radius between the elemental area and the axis. Imply

Therefore for a uniform homogenous thin plate, the mass moment of inertia about axis a can be expressed in terms of area moment of inertia about axis a. Imply
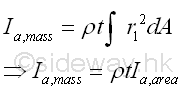
For the mass moment of inertia about axis b, which is perpendicular to axis a.
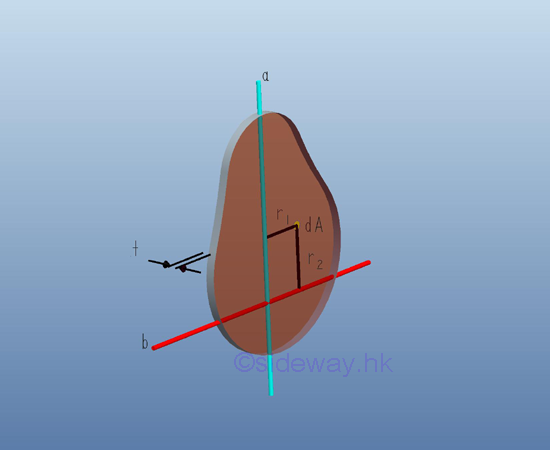
Similarly, the mass moment of inertia about axis b, which is perpendicular to axis a can be expressed in terms of the area moment of inertia about b as in the rectangular moments of inertia. Imply
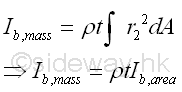
And for the mass moment of inertia about axis c, which is perpendicular to the plate and pass through the intersection of axes a and b.
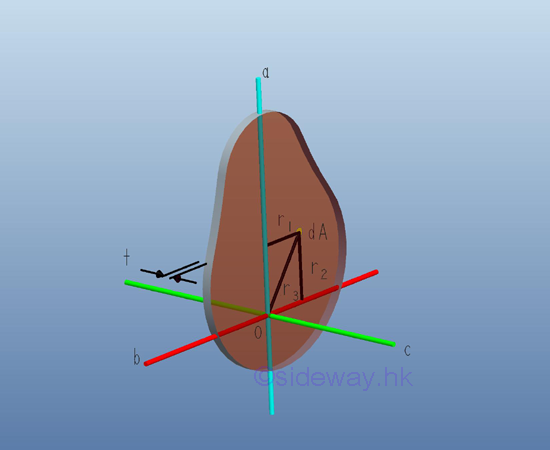
Similarly, the mass moment of inertia about axis c, which is perpendicular to the plate and pass through the intersection of axes a and b can be expressed in term of the area polar moment of inertia about pole O in magnitude but the mass moment of inertia is concerning about the inertia of rotation about the axis c. Imply
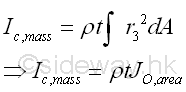
Therefore, from the relation between the rectangular area moments of inertia and the polar area moment of inertia, the relationship for the rectangular mass moments of inertia of a unform homogenous thin plate is
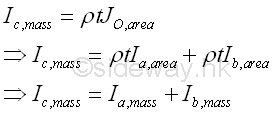
Moment of Inertia of Thin Circular Plate
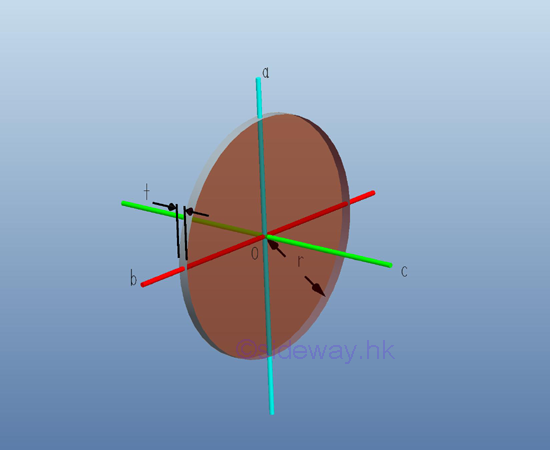
For a thin uniform homogenous circular plate, the mass moment of inertia about the rectangular coordinate axes, a and b, passing through the centre of gravity of the circular plate can be obtained from the area moment of inertia. Imply
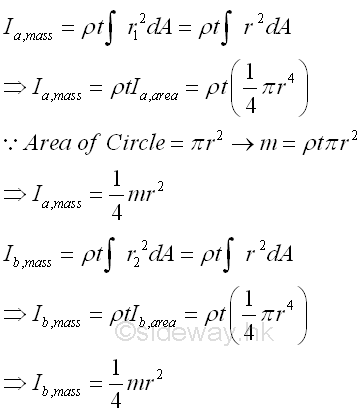
Similarly, the mass moment of inertia about axis c perpendicular to the rectangular coordinate axes a and b can also be obtained from the relation between the polar area moment of inertia and the rectangular area moment of inertia. Imply
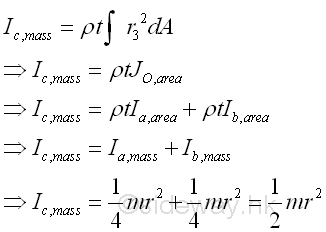
Moment of Inertia of Thin Rectangular Plate
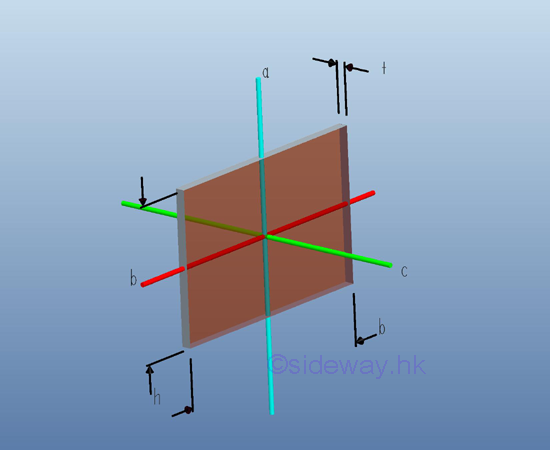
For a thin uniform homogenous rectangular plate, the mass moment of inertia about the rectangular coordinate axes, a and b, passing through the centre of gravity of the circular plate can be obtained from the area moment of inertia. Imply
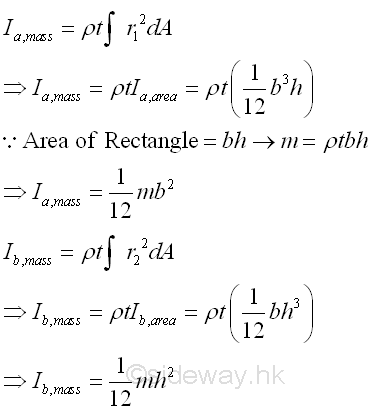
Similarly, the mass moment of inertia about axis c perpendicular to the rectangular coordinate axes a and b can also be obtained from the relation between the polar area moment of inertia and the rectangular area moment of inertia. Imply
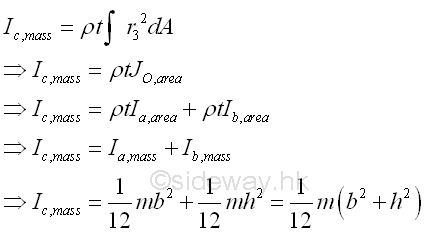
©sideway
ID: 121100002 Last Updated: 10/16/2012 Revision: 0 Ref:
References
- I.C. Jong; B.G. rogers, 1991, Engineering Mechanics: Statics and Dynamics
- F.P. Beer; E.R. Johnston,Jr.; E.R. Eisenberg, 2004, Vector Mechanics for Engineers: Statics
Latest Updated Links
- Philips CL400 Ceiling Light 36W(last updated On 11/2/2025)
- Philips CL400 Ceiling Light 24W(last updated On 11/1/2025)
- Philips CL400 Ceiling Light 13W(last updated On 10/30/2025)
- Ikea TISKEN basket(last updated On 10/29/2025)
- Ikea TISKEN towel rack(last updated On 10/28/2025)
- Ikea REXBEGONIA mattress protector(last updated On 10/27/2025)
- Ikea KEJSAROLVON mattress protector(last updated On 10/26/2025)
- Ikea KVARNVEN ergonomic pillow(last updated On 10/25/2025)
- Ikea BRUKSVARA pocket prung mattress(last updated On 10/24/2025)
- Ikea VÅGSTRANDA pocket sprung mattress super firm(last updated On 10/23/2025)
- Ikea VITVAL underbed(last updated On 10/22/2025)

 Nu Html Checker
Nu Html Checker  53
53  na
na  na
na
Home 5
Business
Management
HBR 3
Information
Recreation
Hobbies 8
Culture
Chinese 1097
English 339
Travel 18
Reference 79
Hardware 25![]()
Computer
Hardware 259
Software
Application 213
Digitization 37
Latex 52
Manim 205
KB 1
Numeric 19
Programming
Web 289
Unicode 504
HTML 66
CSS 65
SVG 46
ASP.NET 270
OS 431
DeskTop 7
Python 72
Knowledge
Mathematics
Formulas 8
Set 1
Logic 1
Algebra 84
Number Theory 206
Trigonometry 31
Geometry 34
Calculus 67
Engineering
Tables 8
Mechanical
Rigid Bodies
Statics 92
Dynamics 37
Fluid 5
Control
Acoustics 19
Natural Sciences
Matter 1
Electric 27
Biology 1
