Content
Moment of Inertia of Common Shape
Moment of Inertia of a
Mass of Homogeneous Body
Moment of Inertia of Slender Rod
Moment of Inertia of
Circular Cylinder
Moment of Inertia of Rectangular Prism
Moment of Inertia of
Circular Cone
Moment of Inertia of Sphere
Moment of Inertia of Common Shape
In general, the second moment of mass in space about an axis can be determined by
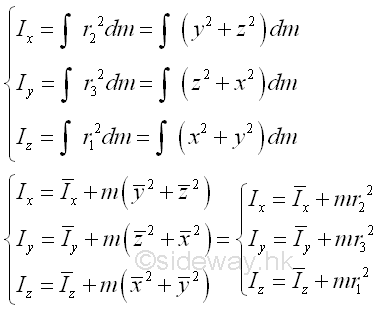
Moment of Inertia of a Mass of Homogeneous Body
Moment of Inertia of Slender Rod
Consider a slender homogenous circular rod of length L with uniform cross-sectional area A and homogenouse material density ρ. Both the cross-sectional area and the material density are constant over the lenght. Since the cross-sectional radius r is much smaller than the length of slender rod, the mass and the elemental mass of the slender rod can be expressed in terms of the mass per unit length, if the reference axis lies in centre of gravity of the slender rod, the mass moment of inertia of the slender rod with respect to an centroidal axis can be expressed as the elemental mass on the axial axis with the distance x as the radius between the elemental mass and the reference axis. Imply
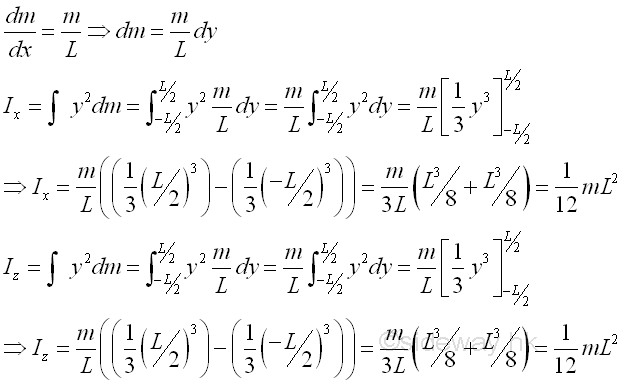
Moment of Inertia of Circular Cylinder
Consider a homogenous circular cylinder of length L with uniform cross-sectional area A of radius r and homogenouse material density l. Both the cross-sectional area and the material density are constant over the lenght, the mass and the elemental mass of the circular cylinder can be expressed in terms of the volume of the circular cylinder. Since the cross-sectional radius r cannot be neglected, the actual distance between the elemental mass and the reference axis should be used. The moments of inertia about axes x and z, can be determined by parallel-axis theorem. Imply
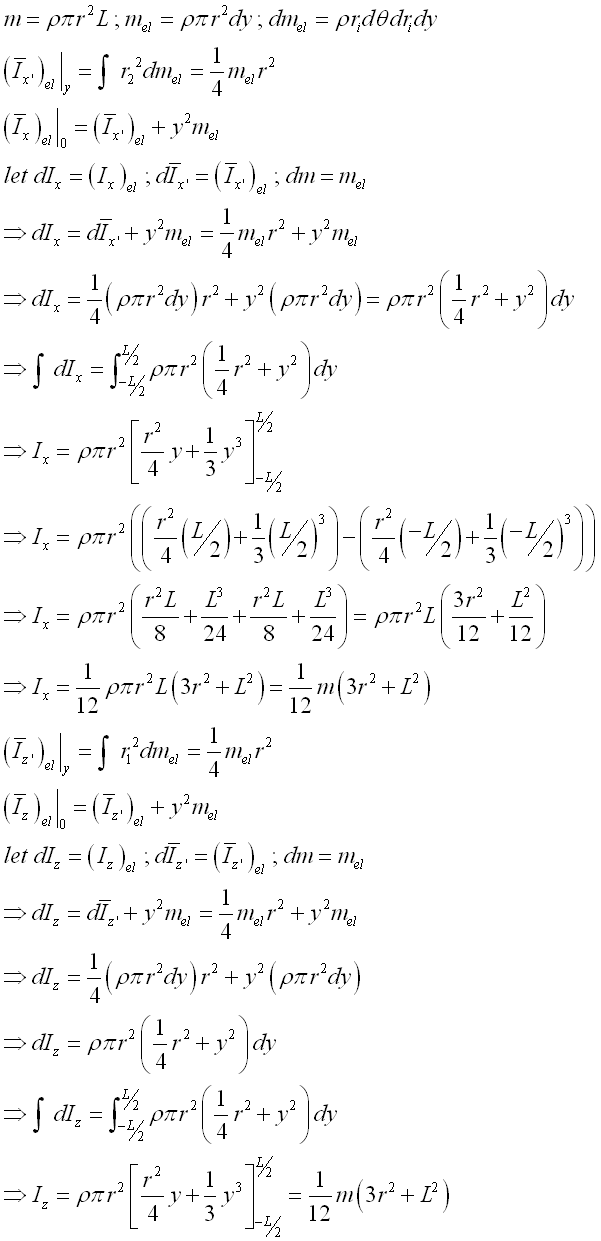
And the moments of inertia about axis y can also be determined by parallel-axis theorem. Imply
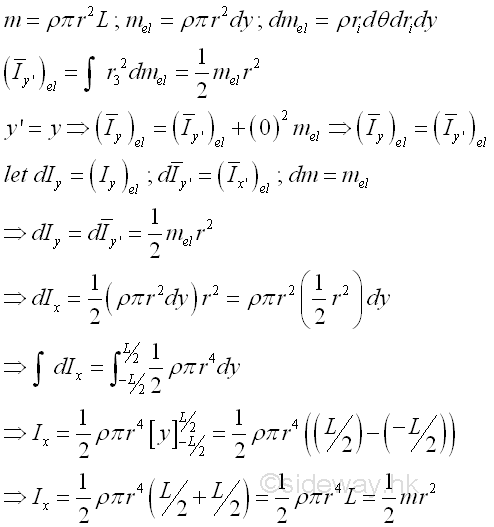
Moment of Inertia of Rectangular Prism
Consider a homogenous rectangular prism of length L with uniform cross-sectional area A of height h, width b and homogenouse material density l. Both the cross-sectional area and the material density are constant over the lenght, the mass and the elemental mass of the rectangular prism can be expressed in terms of the volume of the rectangular prism. Since the cross-sectional dimensions cannot be neglected, the actual distance between the elemental mass and the reference axis should be used. The moments of inertia about axes x and z, can be determined by parallel-axis theorem. Imply
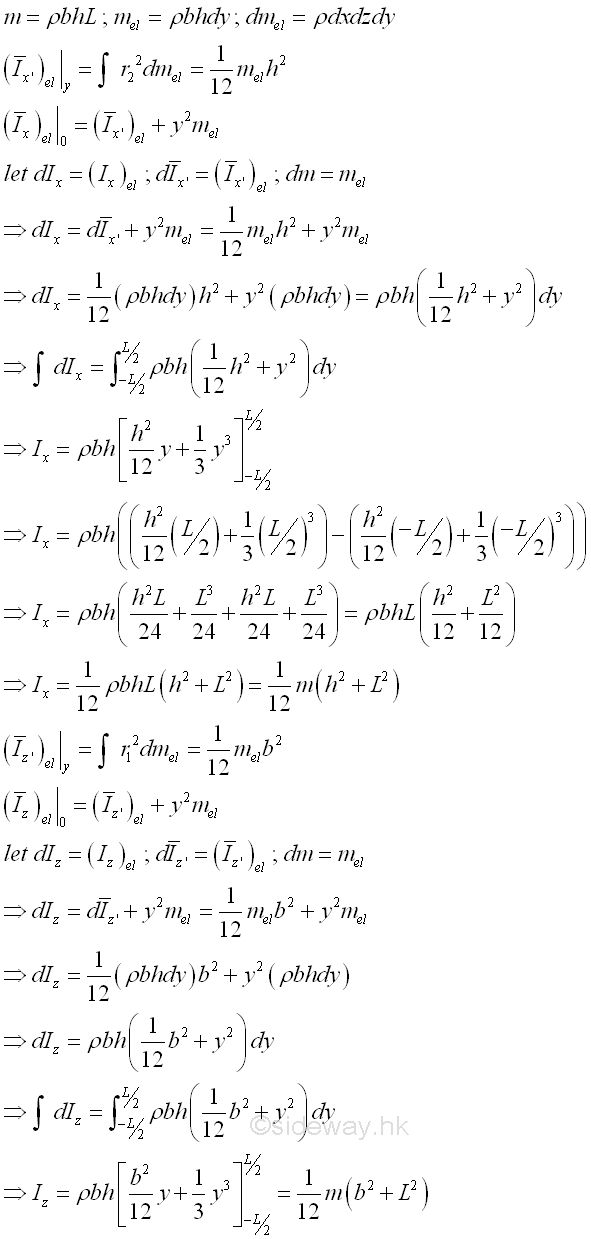
And the moments of inertia about axis y can also be determined by parallel-axis theorem. Imply
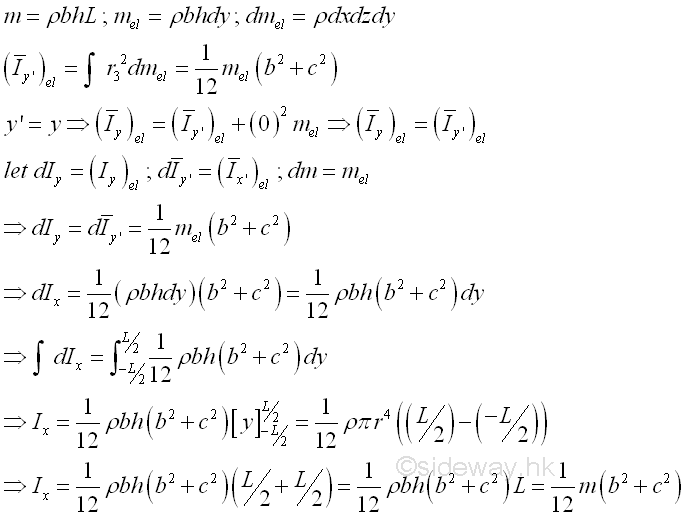
Moment of Inertia of Circular Cone
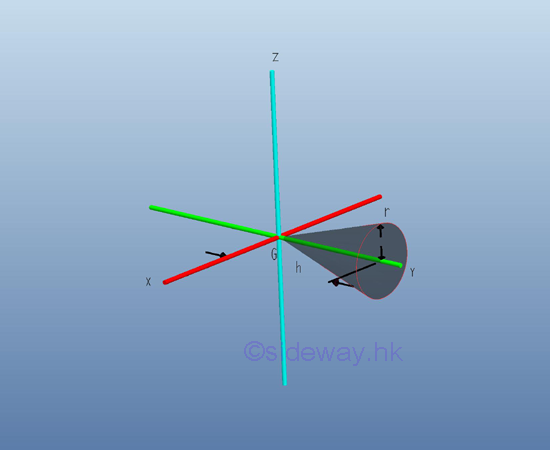
Consider a homogenous circular cone of height h with base area A of radius r and homogenouse material density l. The material density is a constant, the mass and the elemental mass of the circular cone can be expressed in terms of the volume of the circular cone. Since the radius r of the base area cannot be neglected, the actual distance between the elemental mass and the reference axis should be used. The moments of inertia about axes x and z, can be determined by parallel-axis theorem. Imply
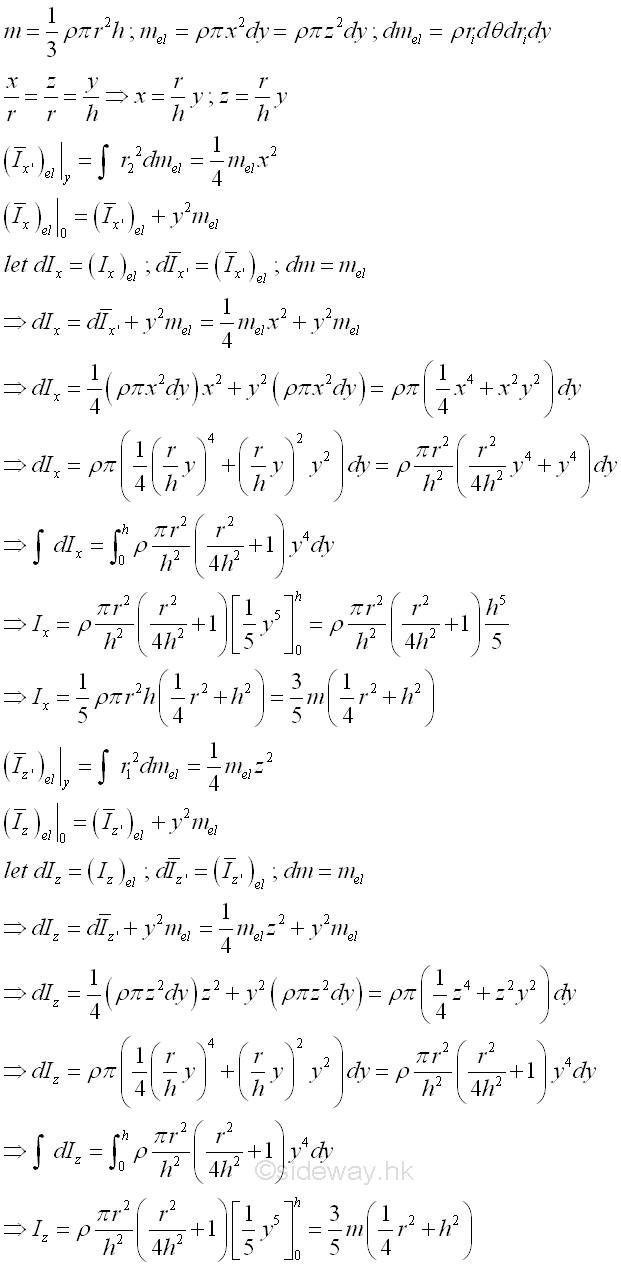
And the moments of inertia about axis y can also be determined by parallel-axis theorem. Imply
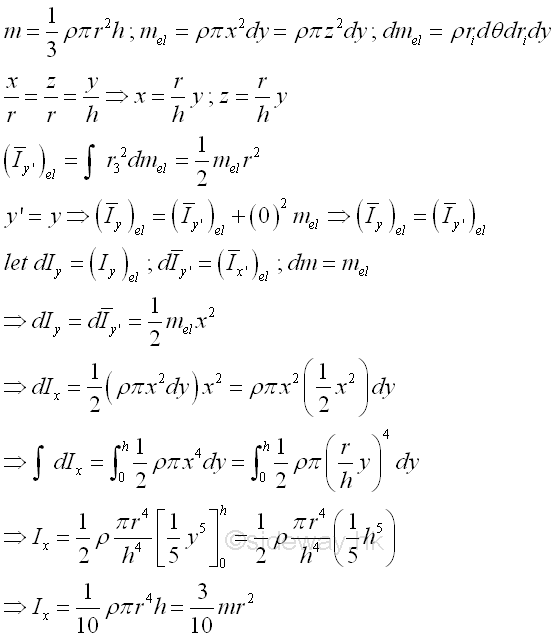
Moment of Inertia of Sphere
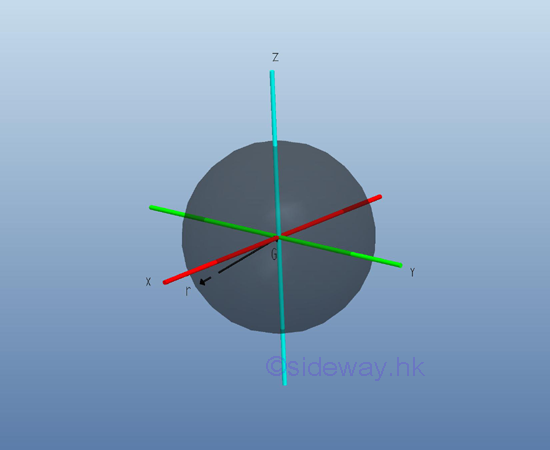
Consider a homogenous sphere of radius r and homogenouse material density l. The material density is a constant, the mass and the elemental mass of the circular cone can be expressed in terms of the volume of the circular cone. Since the radius r of the sphere area cannot be neglected, the actual distance between the elemental mass and the reference axis should be used. The moments of inertia about axes x, y and z, can be determined by triple integration. Imply
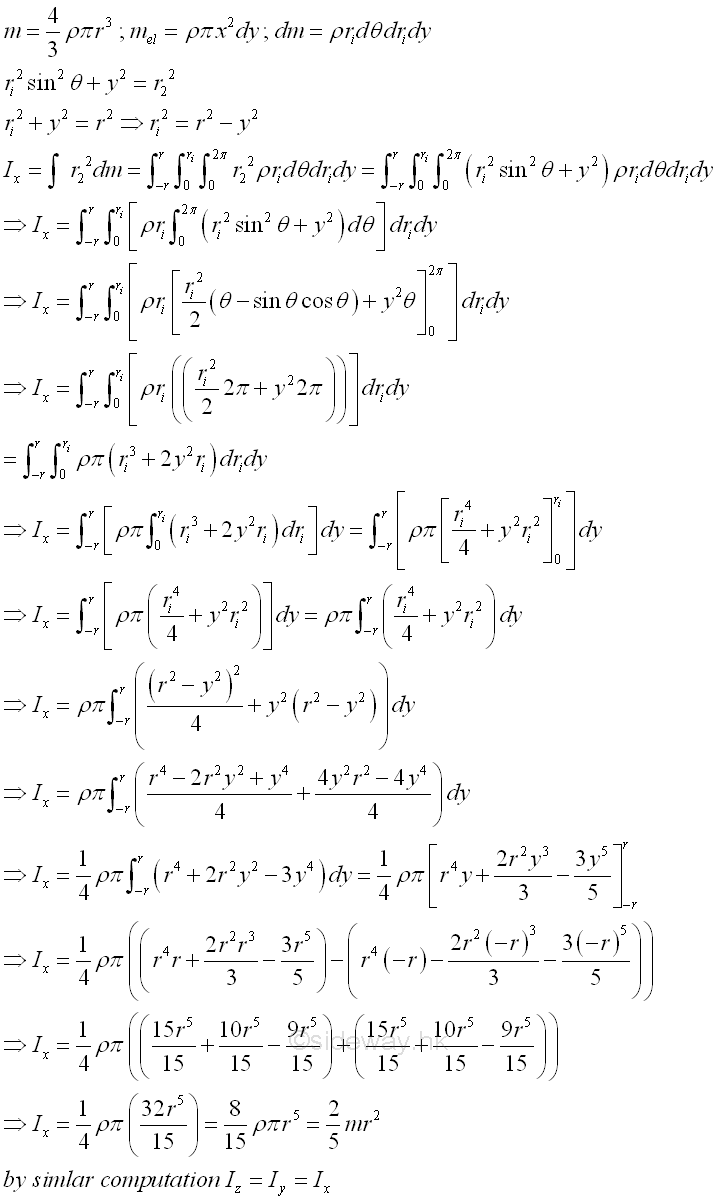
©sideway
ID: 121100086 Last Updated: 11/14/2012 Revision: 0 Ref:
References
- I.C. Jong; B.G. rogers, 1991, Engineering Mechanics: Statics and Dynamics
- F.P. Beer; E.R. Johnston,Jr.; E.R. Eisenberg, 2004, Vector Mechanics for Engineers: Statics
Latest Updated Links
- Panasonic SR-CK05 RiceCooker CW-HZ70AA(last updated On 11/17/2025)
- Panasonic Hood Structure Ventilating Fan Blade Diameter: 8in FV-20WH307 CW-HZ70AA(last updated On 11/16/2025)
- Panasonic Window Mount Thermo Ventilator FV-30BW2H CW-HZ70AA(last updated On 11/15/2025)
- Panasonic Inverter PRO Inverter Window Heatpump Air-Conditioner (3/4 HP) CW-HZ70AA(last updated On 11/14/2025)
- Panasonic Inverter Window-Split Type Cooling Only Air-Conditioner (1 HP) CS-U9YWA(last updated On 11/13/2025)
- Panasonic Inverter Steam and Grill_Microwave Oven 27L NN_DS59NB(last updated On 11/12/2025)
- Panasonic KY-C223B Induction Cooker(last updated On 11/11/2025)
- Focus M41 Single lever kitchen mixer 160(last updated On 11/10/2025)
- Focus Single lever basin mixer 230(last updated On 11/9/2025)
- Precision Start Thermostat shower mixer(last updated On 11/8/2025)
- Tempesta 100 Shower Rail Set 3 sprays(last updated On 11/7/2025)

 Nu Html Checker
Nu Html Checker  53
53  na
na  na
na
Home 5
Business
Management
HBR 3
Information
Recreation
Hobbies 8
Culture
Chinese 1097
English 339
Travel 18
Reference 79
Hardware 40
Computer
Hardware 259
Software
Application 213
Digitization 37
Latex 52
Manim 205
KB 1
Numeric 19
Programming
Web 289
Unicode 504
HTML 66
CSS 65
SVG 46
ASP.NET 270
OS 431
DeskTop 7
Python 72
Knowledge
Mathematics
Formulas 8
Set 1
Logic 1
Algebra 84
Number Theory 206
Trigonometry 31
Geometry 34
Calculus 67
Engineering
Tables 8
Mechanical
Rigid Bodies
Statics 92
Dynamics 37
Fluid 5
Control
Acoustics 19
Natural Sciences
Matter 1
Electric 27
Biology 1
