Content
Second Moment of Mass
Moment of Inertia of a
Mass of Body
Radius of Gyraton of Mass of a Body
Moment of Inertia of Mass in Space
Parallel-Axis Thorem of Mass Moment of Inertia
Mass Moment of Inertia of a Three Dimensional Body of Homogenous Material
Second Moment of Mass
In general, the second moment of mass in space about an axis is also equal to the summation of the products of the square of the distance between the elemental mass and the reference axis, and the elemental mass over an area. As the second moment of mass is usually refered to the rotation, the distance between the elemental mass and the rotating axis is denoted by r. Imply
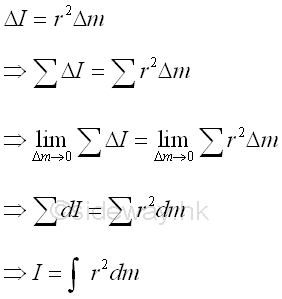
Moment of Inertia of a Mass of Body
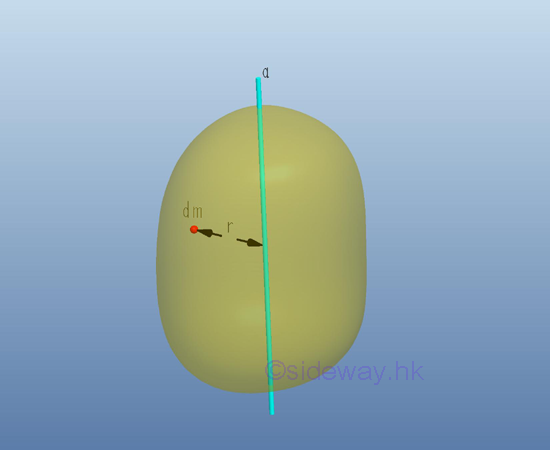
Consider a body of mass m, the moment of inertia of mass of the solid body with respect to the axis a can also be determined by dividing the body into elemental mass Δm. The total moment of inertia of mass of the body, which is equal to the sum of all elemental mass, can then be obtained by taking limit as the number of elemental mass approach infinity. Imply
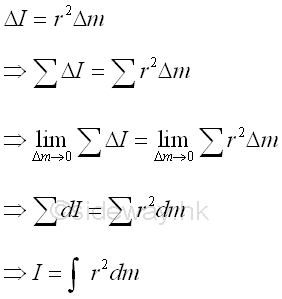
Radius of Gyraton of Mass of a Body
Similarly, the radius of gyraton k of the body is also defined as the distance between the location of an imaginary total mass of the body and the reference axis such that an equivalent second moment of the mass is created by assuming the imaginary total mass of the body is placed at this distance away from the reference axis. Imply
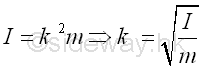
Since the inertia of mass is related to the rotation of the body, the imaginary total mass m, used to represent the body, can be located at the perpendicular distance k anywhere away from the axis a for representing the same gyration or the rotation of the body about the axis a.
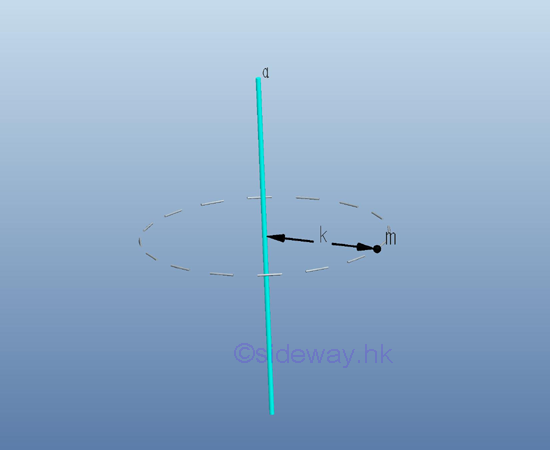
Moment of Inertia of Mass in Space
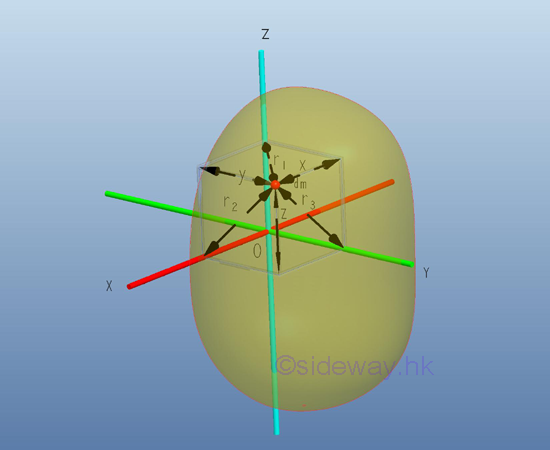
Similar to the polar area moment of inertia in a rectangular coordinate system, the mass moment of inertia about an axis in space can also be expressed in terms of the elemental mass about an axis of the rectangular coordinate axes x, y, and z. as in the rectangular area moments of inertia. Imply
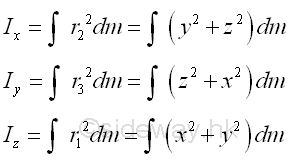
Parallel-Axis Thorem of Mass Moment of Inertia
Consider the same body of mass m with centre of gravity G. Let the rectangular coordinate axes with origin O is XYZ and the parallel centroidal rectangular coordinate axes with origin G, at distance (x,y,z) away from origin O, is X'Y'Z'. Imply
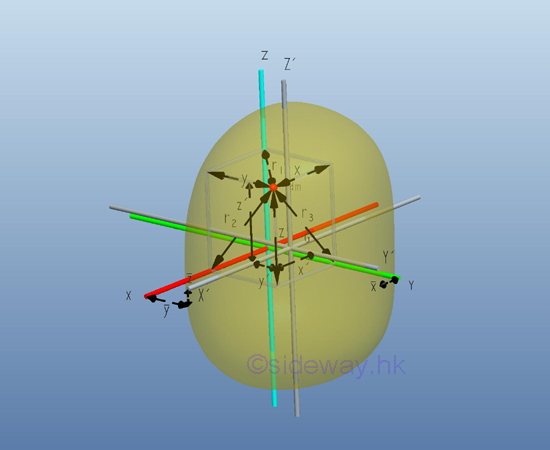
Therefore, the distance x,y,z between the elemental mass and the coordinate axes with origin O can be expressed in terms of the distance x', y',z, between the elemental mass and the coordinate axes with origin G. Imply
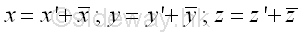
Similarly the mass moments of inertia of the body about the rectangular coordinate axes with origin O can be expressed in terms of the mass moments of inertia of the body about the parallel centroidal rectangular coordinate axes with origin G also. Imply
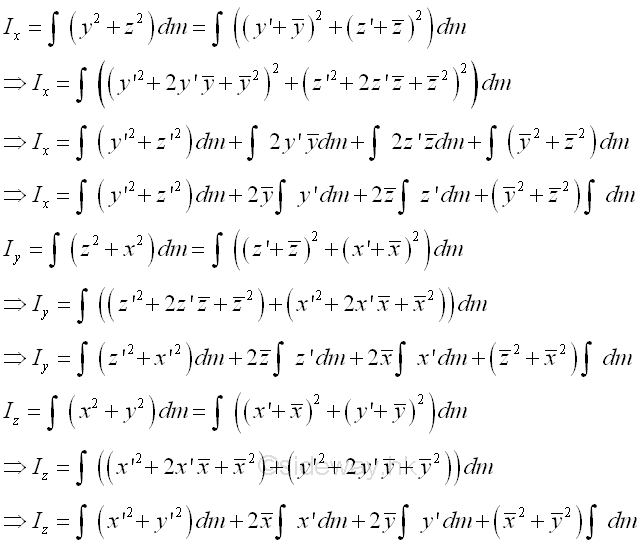
The integral of the moment of inertia I of the mass m about the rectangular axis can be divided into four seperated integrals. The first integral is the centroidal moment of inertia I of the mass. The second and third integrals are the first moment of the mass m about the centroidal axis and the value of the first moment of the mass about the centroidal axis is equal to zero. The fourth integral is equal to the total mass only. Imply
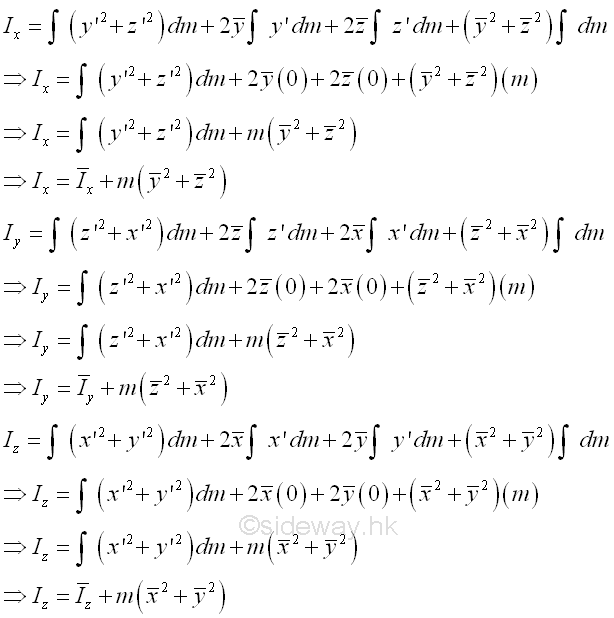
The sum of the square of the rectangular coordinate distance from axes is equal to the square of the distance of the perpendicular displacement from the axes. Imply
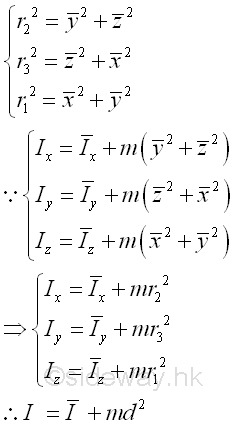
Or the mass moment of inertia can be expressed in terms of the radii of gyration. Imply
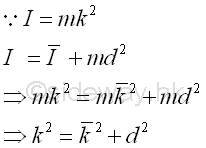
Mass Moment of Inertia of a Three Dimensional Body of Homogenous Material
For a three-dimensional body made of homomgenous material of density ρ, the elemental mass dm can be expressed in terms of the volume of the three dimensional body. In other words, the mass moment of inertia of a three dimensional body of homogenous material density depends on the shape of the three dimensional body only. Imply
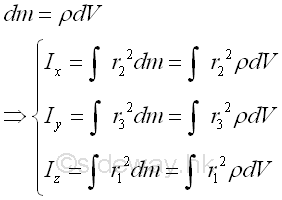
©sideway
ID: 121100085 Last Updated: 11/14/2012 Revision: 0 Ref:
References
- I.C. Jong; B.G. rogers, 1991, Engineering Mechanics: Statics and Dynamics
- F.P. Beer; E.R. Johnston,Jr.; E.R. Eisenberg, 2004, Vector Mechanics for Engineers: Statics
Latest Updated Links
- Travel Singapore Sight Sentosa Resorts World Sentosa(last updated On 1/4/2026)
- Travel Singapore Sight Sentosa HarbourFront(last updated On 1/3/2026)
- Travel Singapore Sight Sentosa(last updated On 1/2/2026)
- Travel Singapore Sight Mandai(last updated On 12/30/2025)
- Travel Singapore Sight Bird Paradise(last updated On 12/30/2025)
- Travel Singapore Sight Singapore Zoo(last updated On 12/30/2025)
- Travel Singapore Sight Rainforest Wild ASIA(last updated On 12/30/2025)
- Travel Singapore Sight River Wonders(last updated On 12/30/2025)
- Travel Singapore Sight Night Safari(last updated On 12/30/2025)
- Travel Singapore Sight Curiosity Cove(last updated On 12/30/2025)
- Travel Singapore Sight Space(last updated On 12/30/2025)

 Nu Html Checker
Nu Html Checker  53
53  na
na  na
na
Home 5
Business
Management
HBR 3
Information
Recreation
Hobbies 9
Culture
Chinese 1097
English 339
Travel 34
Reference 79
Hardware 54
Computer
Hardware 259
Software
Application 213
Digitization 37
Latex 52
Manim 205
KB 1
Numeric 19
Programming
Web 289
Unicode 504
HTML 66
CSS 65
SVG 46
ASP.NET 270
OS 431
DeskTop 7
Python 72
Knowledge
Mathematics
Formulas 8
Set 1
Logic 1
Algebra 84
Number Theory 206
Trigonometry 31
Geometry 34
Calculus 67
Engineering
Tables 8
Mechanical
Rigid Bodies
Statics 92
Dynamics 37
Fluid 5
Control
Acoustics 19
Natural Sciences
Matter 1
Electric 27
Biology 1
