Content
Internal Forces
in Beams
Shear and Bending Moment
Diagrams
Internal Forces in a Cantilever Beam
Shear Diagram
Bending Moment Diagram
Internal Forces in a Simply Supported Beam
Shear Diagram
Bending Moment Diagram
Internal Forces in a Overhanging Beam
Assumption for
Shear and Bending Moment
Diagrams
Shear Diagram
Bending Moment Diagram
Internal Forces in Beams
The shearing forces and bending moments in a statically determinate beam can be determined by the equilibrium equations. Using the standard convention, the distribution of internal forces in a beam can be represented graphically by plotting the values of shear or bending moment against the distance from one end of the beam.
Shear and Bending Moment Diagrams
Internal Forces in a Cantilever Beam
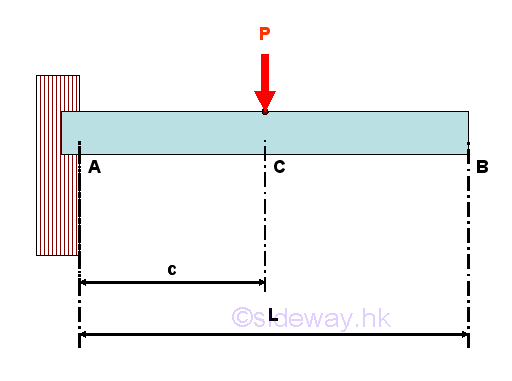
For example, consider a simple cantilevel beam with one applied load applied around the middle of the beam. The free-body diagram of the entire beam is
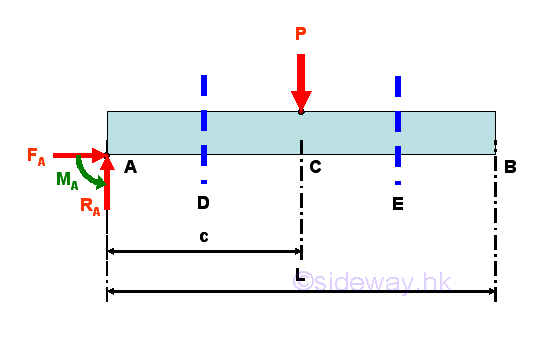
The reactions at the fixed support can be determined by the equilibrium equations.
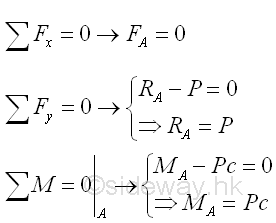
Internal forces can be determined by dividing the beam into two separated free body. Selecting a point D between A and C, i.e. A<D<C
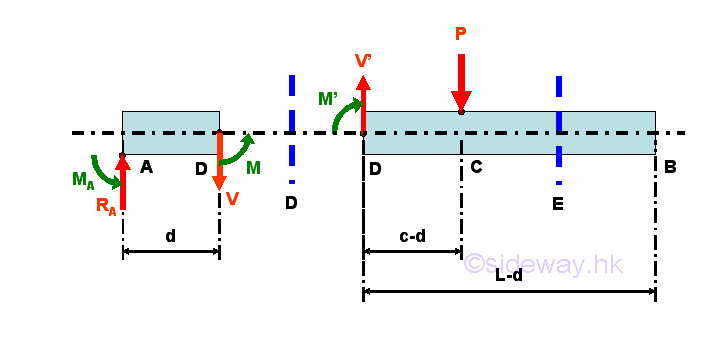
Consider the member section AD of length d, the internal forces at point D are
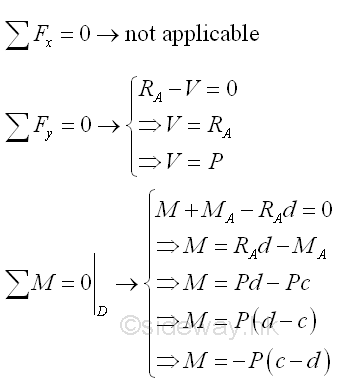
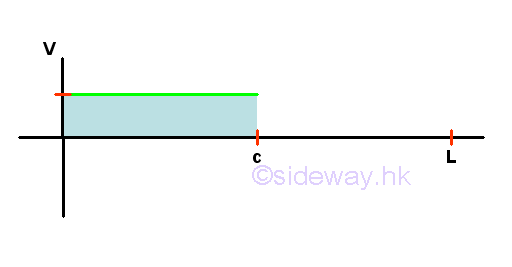
Point D is a random point between A and C. The shear force V is a constant and is equal to P between point A and point D. And bending moment M is a linear function of point D. Therefore bending moment M=-Pc at point A and bending moment M=0 at point C.
Selecting another point E between C and B, i.e. C<E<B
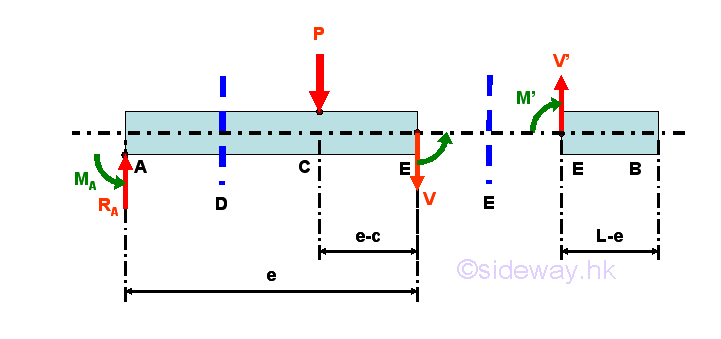
Consider the member section EB of length L-e, the internal forces at point E are
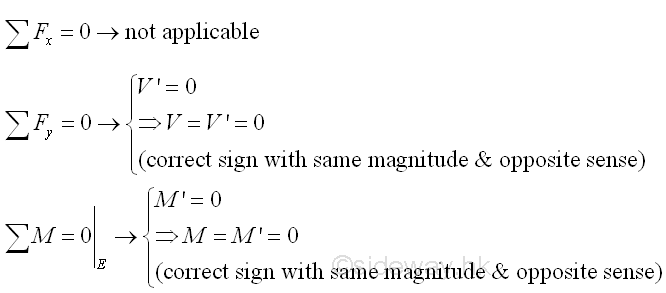
Point E is a random point between C and B. Both the shear force V and bending moment M is equal to zero between point C and point B.
Shear Diagram
Bending Moment Diagram
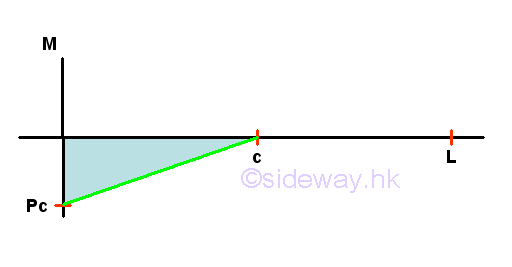
Internal Forces in a Simply Supported Beam
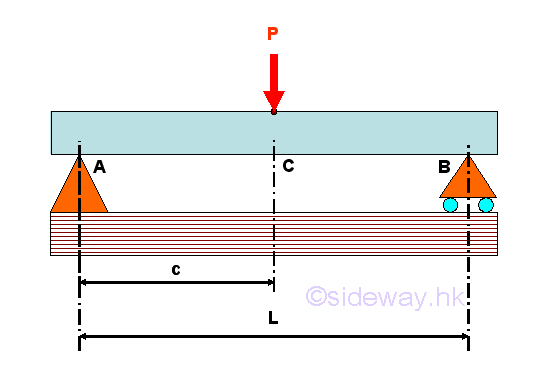
For example, consider a simply supported beam with one applied load applied around the middle of the beam. The free-body diagram of the entire beam is
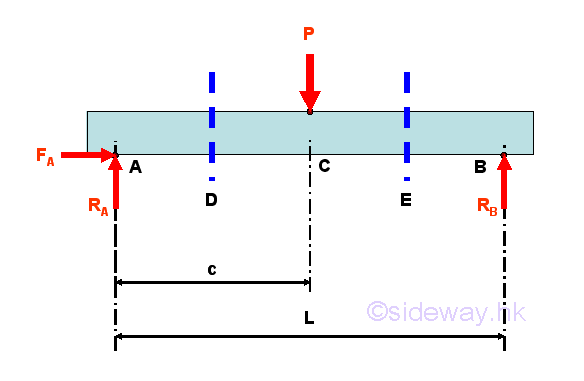
The reactions at the hinged and roller supports can be determined by the equilibrium equations.
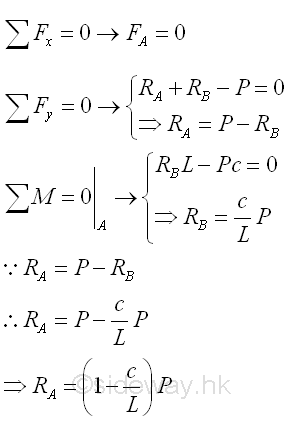
Internal forces can be determined by dividing the beam into two separated free body. Selecting a point D between A and C, i.e. A<D<C
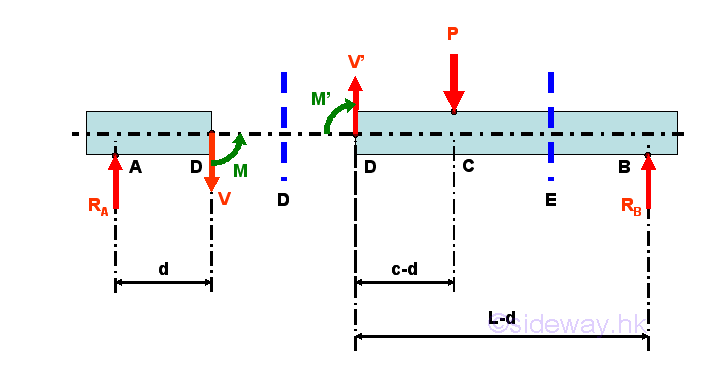
Consider the member section AD of length d, the internal forces at point D are
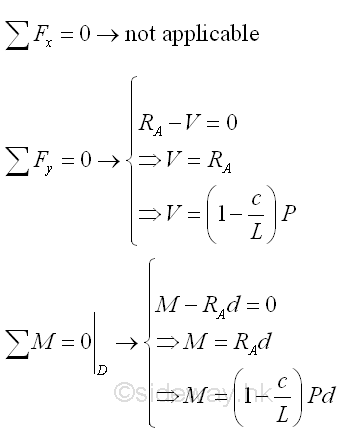
Point D is a random point between A and C. The shear force V is a constant and is equal to (1-c/L)P between point A and point C. And bending moment M is a linear function of point D. Therefore bending moment M=0 at point A and bending moment M=(1-c/L)Pc at point C.
Selecting another point E between C and B, i.e. C<E<B
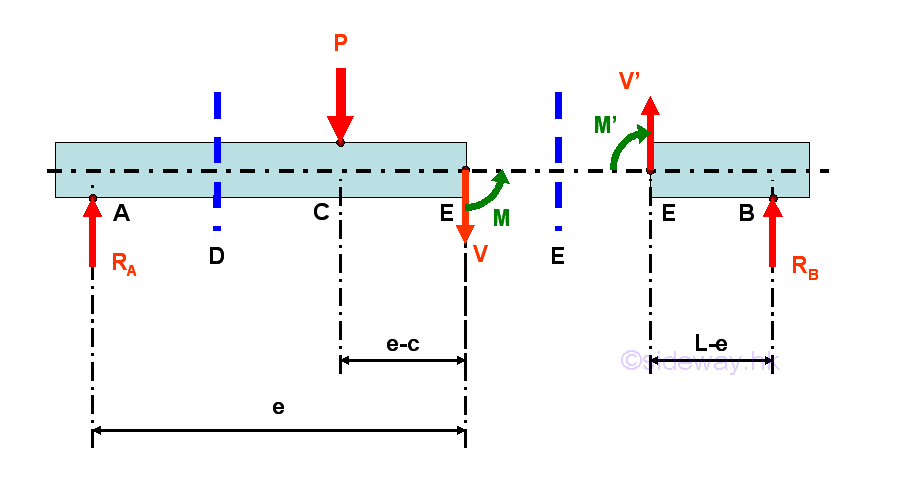
Consider the member section EB of length L-e, the internal forces at point E are

Point E is a random point between C and B. The shear force V is a constant and is equal to -(c/L)P between point C and point B. And bending moment M is a linear function of point E. Therefore bending moment M=(1-c/L)Pc at point C and bending moment M=0 at point B
Shear Diagram
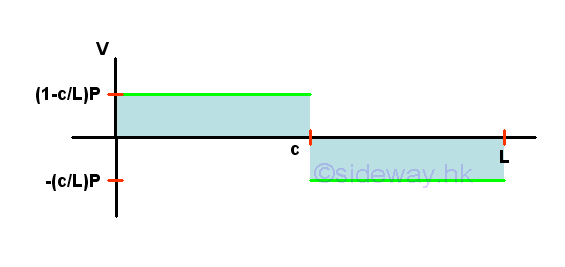
Bending Moment Diagram
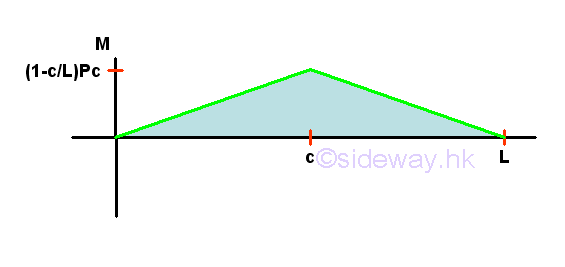
Internal Forces in a Overhanging Beam
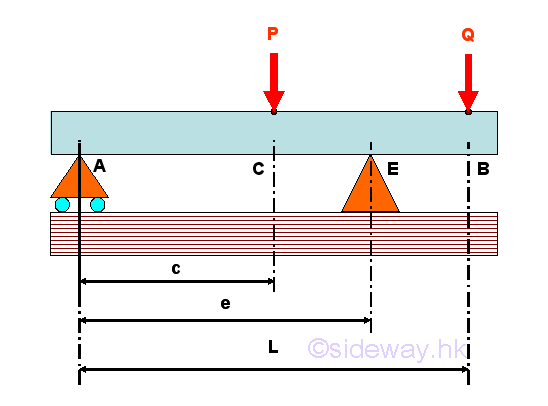
For example, consider a overhanging beam with two applied load applied around the middle and the free end of the beam. The free-body diagram of the entire beam is
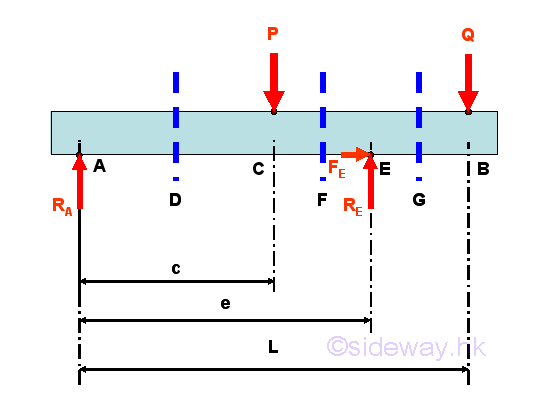
The reactions at the roller and hinged supports can be determined by the equilibrium equations.
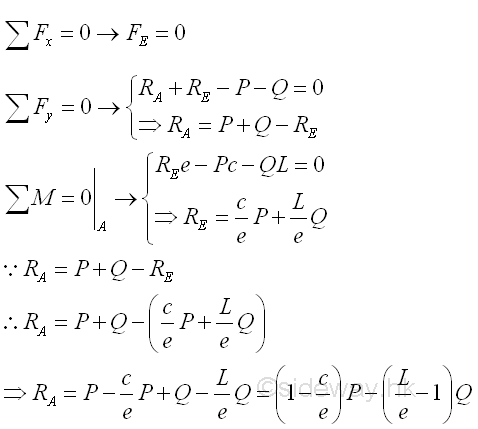
Internal forces can be determined by dividing the beam into two separated free body. Selecting a point D between A and C, i.e. A<D<C
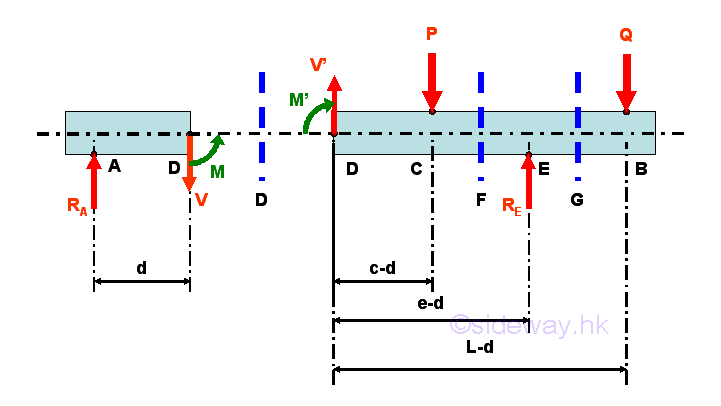
Consider the member section AD of length d, the internal forces at point D are
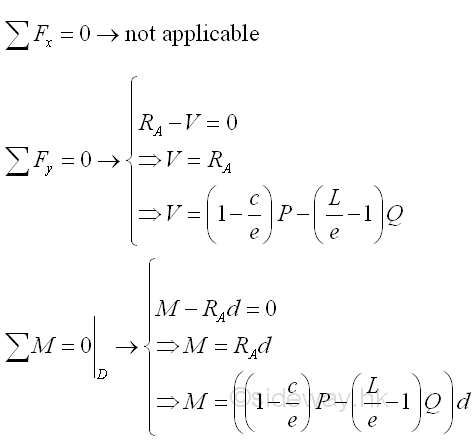
Point D is a random point between A and C. The shear force V is a constant and is equal to ((1-c/e)P-(L/e-1)Q) between point A and point C. And bending moment M is a linear function of point D. Therefore bending moment M=0 at point A and bending moment M=((1-c/e)P-(L/e-1)Q)c at point C.
Selecting another point F between C and E, i.e. C<F<E
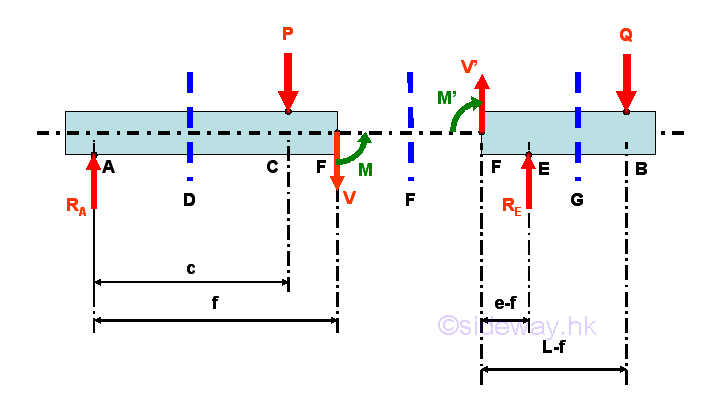
Consider the member section AF of length f, the internal forces at point F are
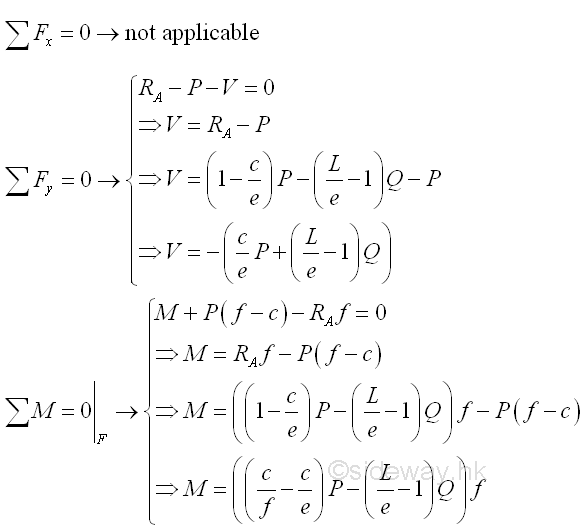
Point F is a random point between C and E. The shear force V is a constant and is equal to (-(c/e)P-(L/e-1)Q) between point C and point E. And bending moment M is a linear function of point F. Therefore bending moment M=((1-c/e)P-(L/e-1)Q)c at point C and bending moment M=-Q(L-e) at point E.
Selecting another point G between E and B, i.e. E<G<B
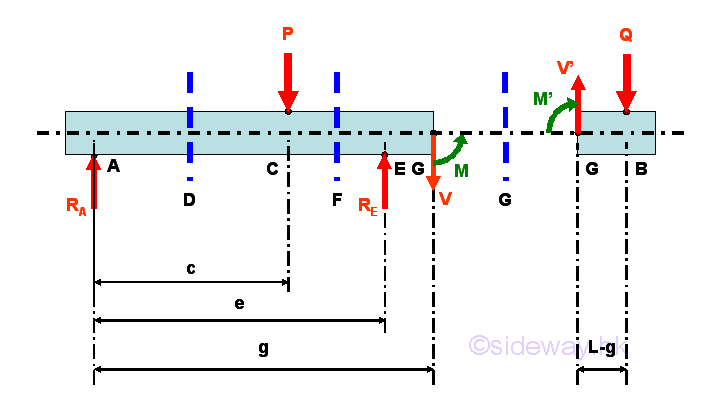
Consider the member section GB of length L-g, the internal forces at point G are

Point G is a random point between E and B. The shear force V is a constant and is equal to Q between point E and point G. And bending moment M is a linear function of point G. Therefore bending moment M=-Q(L-e) at point E and bending moment M=0 at point B.
Assumption for Shear and Bending Moment Diagrams
Since length L is greater than length e, the reaction force RA at point A may be negative if load Q term is greater than load P term. For normal practical applications, the reaction force RA at point A is usually pointing upward. Therefore, the reaction force RA at point A is assumed positive in plotting the shear and bending moment diagrams.
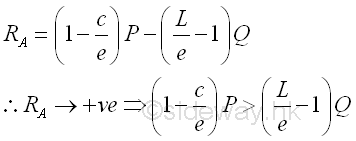
Shear Diagram
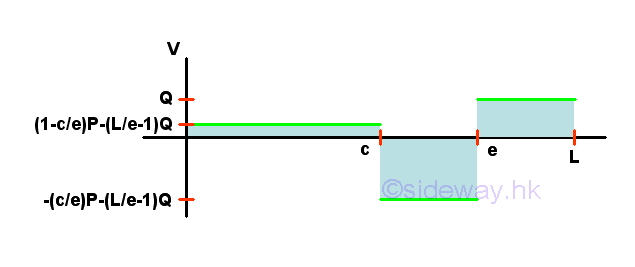
Bending Moment Diagram
©sideway
ID: 120800023 Last Updated: 8/29/2012 Revision: 0 Ref:
References
- I.C. Jong; B.G. rogers, 1991, Engineering Mechanics: Statics and Dynamics
- F.P. Beer; E.R. Johnston,Jr.; E.R. Eisenberg, 2004, Vector Mechanics for Engineers: Statics
Latest Updated Links
- Legrand Galion(last updated On 12/2/2025)
- Schneider Electric AvatarOn(last updated On 12/1/2025)
- Alfalux(last updated On 11/30/2025)
- Novabell(last updated On 11/29/2025)
- TownGas NJW12RM1(last updated On 11/28/2025)
- SamSung 42" OLED TV S90F 4K(last updated On 11/27/2025)
- Tefal KI7208 GLASS VISION KETTLE(last updated On 11/26/2025)
- Tefal BL83SD PerfectMix Cook Blender(last updated On 11/25/2025)
- Tefal KI7208 GLASS VISION KETTLE(last updated On 11/24/2025)
- Hitachi RD-290GX Dehumidifier(last updated On 11/23/2025)
- Hitachi RD-290GX Dehumidifier(last updated On 11/22/2025)

 Nu Html Checker
Nu Html Checker  53
53  na
na  na
na
Home 5
Business
Management
HBR 3
Information
Recreation
Hobbies 9
Culture
Chinese 1097
English 339
Travel 18
Reference 79
Hardware 54
Computer
Hardware 259
Software
Application 213
Digitization 37
Latex 52
Manim 205
KB 1
Numeric 19
Programming
Web 289
Unicode 504
HTML 66
CSS 65
SVG 46
ASP.NET 270
OS 431
DeskTop 7
Python 72
Knowledge
Mathematics
Formulas 8
Set 1
Logic 1
Algebra 84
Number Theory 206
Trigonometry 31
Geometry 34
Calculus 67
Engineering
Tables 8
Mechanical
Rigid Bodies
Statics 92
Dynamics 37
Fluid 5
Control
Acoustics 19
Natural Sciences
Matter 1
Electric 27
Biology 1
